三峡电站流量变率对两坝间通航水流影响的三维计算分析

黄明海，李 飞，史德亮，邢领航，唐文坚

(1.长江科学院水力学研究所，武汉 430010;2.长江水利委员会a.规划计划局;b.国际合作与科技局，武汉 430010)

1 研究背景

葛洲坝水利枢纽建成蓄水后，两坝间河段处于水库常年回水区，但因葛洲坝为低水头水利枢纽，年内不同时期河道表现“人工水库”与“天然河道”的双重特性。在中、低水期，水流较平缓，流速和比降均不大，船舶航行无多大困难;在汛期，两坝间航道既受三峡大坝下泄流量和葛洲坝坝前水位影响，又受峡谷河段河床地形条件制约，随着入库流量的增加，河床过水断面增加有限，水流湍急，流态紊乱，呈现出天然河道特性，加上汛期水库降低水位运行，三峡大坝泄洪时两坝间狭窄河段水流不畅，流速、比降急剧增大、泡漩横流丛生、流态极乱，通航条件迅速恶化，给万吨级船队的通航带来极大的困难［1－2］。

三峡电站在泄洪和日调节时产生的非恒定流，使得两坝间的航行条件更为复杂。其中电站机组开启过程下泄流量变率产生的非恒定流对两坝间河段通航水流条件的影响，是电站调度和管理部门较为关注的问题，值得深入研究。为此，本文针对这一问题采用三维河流数学模型进行计算分析。

2 两坝间河段航道概况

三峡至葛洲坝两坝间河段(以下简称两坝间)约38 km，其中约35 km河段处于西陵峡中，如图1所示。三斗坪至乐天溪为宽谷河段长9.6 km，汛期河面最宽可达1 400 m，河槽多呈复式断面;乐天溪至南津关为峡谷河段，全河段峰回河转、蜿蜒曲折、河谷陡峭、河槽窄深，河床断面多呈“V”型或“U”型，河宽一般200～300 m，在汛期大流量时，水流湍急、流态紊乱、碍航滩险较多，主要位于水田角、喜滩和石牌弯道等河段，是长江上游航道中航行最困难的区段之一［3］。

图1 三峡至葛洲坝两坝间河段河势及典型断面布置Fig.1 River regime and typical section layout of the waterway between TGD and Gezhouba Dam

3 两坝间河段通航水流技术标准

1992年交通部三峡工程航运领导小组办公室以(92)交三峡办字第07号文颁布的《三峡工程通航标准》，供三峡工程设计和科研采用。故两坝间河段航道尺度、通航流量、水位、保证率和通航水力指标采用标准如下。

(1)航道尺度:按通航万吨级船队安全运行需要，渝汉航道尺度标准为，最小航宽(单行)100 m，在弯道应加宽，最小双向航宽是单行航宽的2倍，最小水深3.5 m，远景水深4 m，最小弯曲半径1 000 m(石牌河段不小于800 m)。

(2)通航流量、水位和保证率:三峡水库下游设计最高通航水位74 m，下游设计最低通航水位62 m。通航保证率99%，万吨级船队渝汉直达保证率不低于50%。

(3)通航水力指标:通航水力指标是指船队上驶所能克服的最大流速和局部水面比降。“七五”攻关期间，通过实船试验、原型观测、计算分析、综合比较，制定出万吨级船队汉渝上驶的通航水力指标，见表1。

表1 万吨级船队汉渝直达允许最大流速、比降Table 1 Allowable max.velocity and surface gradient for direct fleet(10 000 t)from Wuhan to Chongqing

4 两坝间通航水流三维数学模型

针对河道通航水流数值模拟以往多采用二维河流数学模型，难以反映水流表面流速，本文采用三维数学模型对两坝间通航水流进行计算分析。

4.1 控制方程

在Boussinesq假设下，考虑各向异性及垂向流速相对较小的假设，浅水河道水流控制方程采用如下形式［4］:

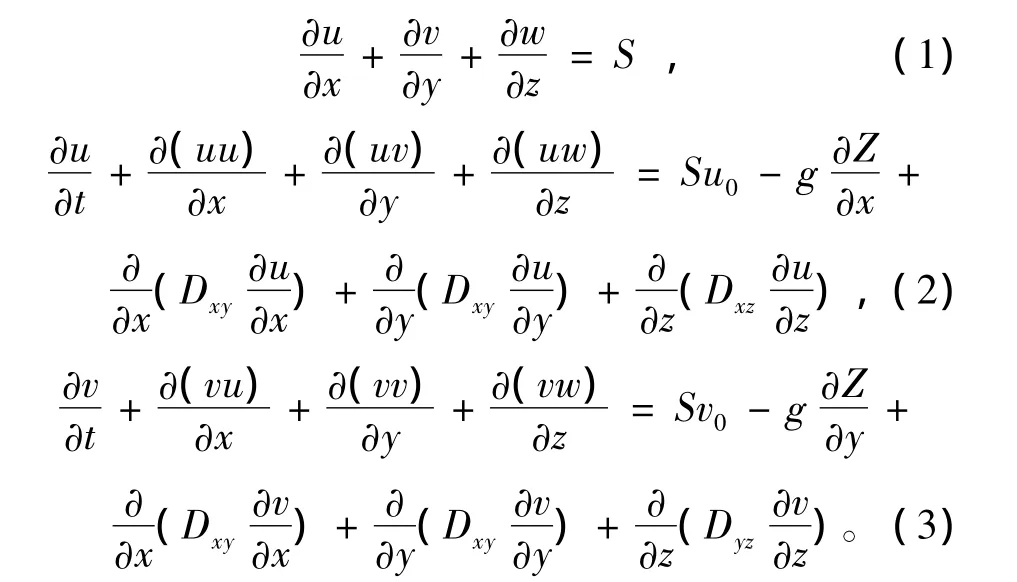
式中:u，v，w 分别为 x，y，z向流速值;Z 为自由水面高程;S为单位水体源汇密度，流入为正，流出为负;u0，v0为源汇处的进出口流速;Dxy，Dyz，Dzx分别为各向紊动黏性系数。

4.2 离散求解与定解条件

针对控制方程进行σ坐标变换和适体曲线坐标变换进行变换，采用有限差分法离散求解。

边界条件:上游取流量为边界条件，下游边界条件恒定流取水位边界，非恒定流取流量边界;河床采用无滑移固壁边界条件。

4.3 计算范围和地形

模拟范围和地形:三峡坝址至葛洲坝坝址长约38 km河道，54北京坐标系(x和y坐标分别偏移－37 500 000 m 和－3 400 000 m)，河道地形1∶2 000，高程转换成吴淞基准，三峡坝址至青鱼嘴6.5 km和三游洞至葛洲坝坝址约12 km两部分河段地形为2005年3月地形，中间部分河段采用2004年10—11月地形，具体地形处理三维效果见图2。

图2 计算范围和地形处理三维效果图Fig.2 Computation region and 3-D terrain

4.4 网格划分

计算网格采用正交曲线四边形网格，其中根据地形作局部加密处理，平面网格单元数量为2 090×107个，垂向网格分10层，网格单元总数约为224万个，网格划分见图3。

图3 计算网格划分示意图Fig.3 Mesh generation

4.5 模型参数率定

根据实测水文资料，采用河道分区率定糙率。

5 模型验证

采用2010年1—4月实测的4个典型下泄流量(分别为 25 000，30 000，35 000，40 000 m3/s)情况下的两坝间恒定流对数学模型进行验证。

5.1 水位验证

各典型流量情况下，两坝间左、右岸关键观测点沿程水位计算结果与实测值比较见图4。从图4中可看出:4种典型下泄流量情况下，计算得出的两坝间河道左岸、右岸水位沿程变化趋势与实测结果一致，观测点水位计算值与实测值吻合较好;4种工况下两者最大差值分别为0.05，0.07，0.12，0.12 m，说明数学模型水位计算结果与实测结果吻合较好。

图4 两坝间左、右岸关键观测点沿程水位分布计算结果与实测值比较Fig.4 Comparison between calculated and measured values of water level at key points along the left and right banks between TGD and Gezhouba dam

5.2 表面流速验证

各典型流量情况下，计算结果得出各典型断面表面流速最大值计算值与实测值最大差值在0.19 m/s以内，最大相对误差在5.7%以内。图5为水田角河段ST2断面表面流速分布计算值与实测值比较，从图中可看出断面表面流速分布计算结果与实测结果基本吻合。

6 机组流量变率影响分析

6.1 机组开启速度变化

6.1.1 计算工况

在三峡电站下泄流量为15 000 m3/s、葛洲坝坝前水位63 m的恒定流条件下，分别在1，5，10，15 min时间内，机组下泄流量均匀增加5 000 m3/s。

6.1.2 计算结果分析

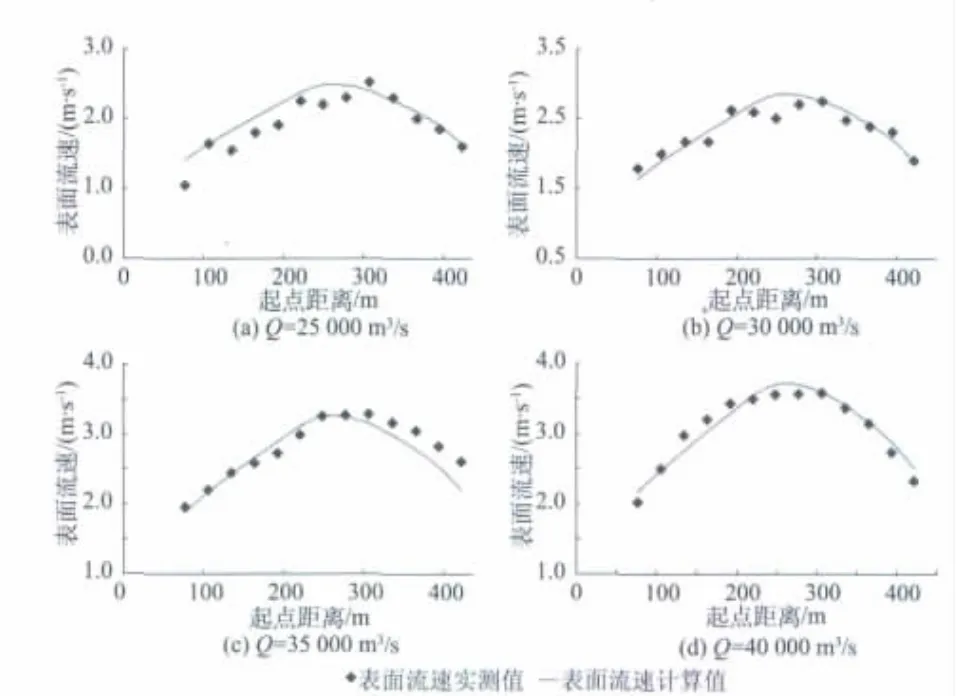
图5 水田角河段ST2断面表面流速分布计算值与实测值比较Fig.5 Comparison between calculated and measured values of surface flow velocity at section ST2 in Shuitianjiao segment

水田角河段为两坝间通航最困难河段，且ST2断面流速最大，本文为此以此河段及其ST2断面为主要分析对象。

计算结果表明:机组分别在 1，5，10，15 min时间内下泄流量增加5 000 m3/s情况下，水田角河段ST1—ST2断面水面瞬时最大比降分别为3.13‱，2.11‱，1.70‱，1.61‱，比初始恒定流比降1.03‱增大2.10‱、1.08‱、0.67‱和0.58‱;ST2 断面瞬时最大表面流速分别为2.29，2.26，2.22，2.20 m/s，比该断面初始恒定流最大表面流速1.76 m/s增大0.53，0.50，0.46，0.44 m/s。

图6给出了水田角河段水面比降、断面最大表面流速与机组不同开启时间关系曲线，结合图中曲线可看出:机组开启时间越短，水田角河段水面比降增幅越大，但ST2断面瞬时最大表面流速增幅则为线性增加;若以比降2‱和表面流速2.3 m/s作为通航水力指标，在机组初始下泄流量为15 000 m3/s、机组开启时间大于6 min增加下泄流量5 000 m3/s时，该河段满足万吨级船队通航要求。

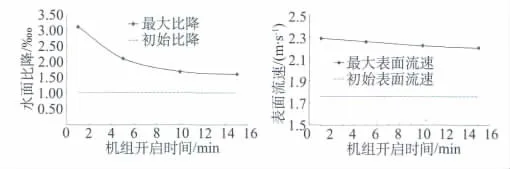
图6 水田角河段水面比降、断面最大表面流速与机组不同开启时间关系曲线Fig.6 Relation of the operation time of power units respectively with the surface gradient and the max.surface velocity in Shuitianjiao segment

图7为机组开启时间变化情况下水田角河段水面比降、断面最大表面流速随时间变化过程曲线，从图可知:在机组开启13～15 min后，水田角河段水面比降以及ST1和ST2断面流速开始增大，不同机组开启时间情况下，两断面最大表面流速变化幅度相近，但该河段水面比降则随机组开启速度的增加而增大。

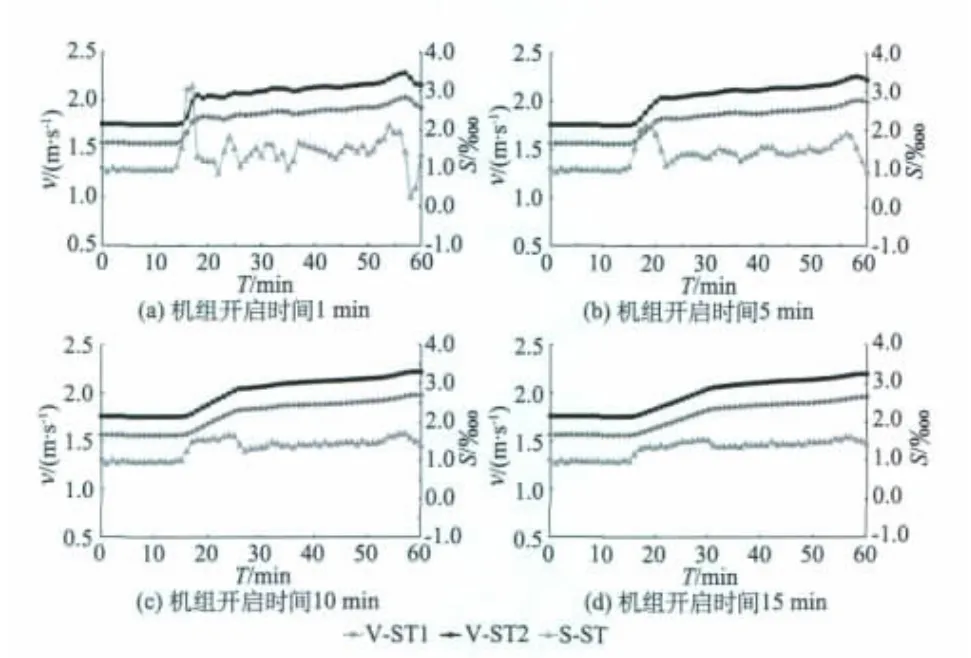
图7 水田角河段水面比降、断面最大表面流速随时间变化过程曲线(机组开启时间变化)Fig.7 Variations of surface gradient and max.surface velocity at Shuitianjiao segment against the operation time of power units

6.2 机组开启流量变化

6.2.1 计算工况

在三峡电站下泄流量为20 000 m3/s、葛洲坝坝前水位63 m的恒定流条件下，在15 min时间内，机组下泄流量分别均匀增加 1 000，2 000，3 000，4 000，5 000 m3/s。

6.2.2 计算结果分析

图8给出了水田角河段水面比降、ST2断面最大表面流速与机组不同开启流量关系曲线，从图中曲线可看出:水田角河段水面比降和ST2断面瞬时最大表面流速的增幅随下泄流量增加线性增加;在初始下泄流量为20 000 m3/s时，在15 min时间内增加上述5种机组下泄流量，水田角河段最大水面比降和ST2断面瞬时最大表面流速，与表1中水面比降和表面流速指标对照不能满足万吨级船队通航要求。

图8 水田角河段水面比降、ST2断面最大表面流速与机组开启流量关系曲线Fig.8 Variations of surface gradient and maximum surface velocity in Shuitianjiao segment against the discharge caused by the turn-on of power units

7 结语

(1)建立了三峡至葛洲坝两坝间通航水流三维数学模型，将数学模型的多个流量级计算结果与实测数据进行了验证，表明所建模型具有较好的计算精度和可靠性。

(2)采用数学模型计算分析了三峡电站机组不同开启速度和不同开启流量情况对典型河段水面比降、表面流速产生的影响及其变化规律。

(3)研究结果表明:机组开启速度变化情况下，机组开启时间越短，水田角河段(通航最困难河段)水面比降增幅越大，ST2断面瞬时最大表面流速增幅则为线性增加;机组开启流量变化情况下，水田角河段水面比降和ST2断面瞬时最大表面流速的增幅随下泄流量线性增加。

［1］孙尔雨，朱庆福.三峡电站调峰对两坝间通航的影响和改善措施［J］.人民长江，1999，(12):8 －9，12.(SUN Er-yu，ZHU Qing-fu.Influence of Peak Modulation of Three Gorges Power Station in on the Navigation Conditions Between the Two Dams and Improvement measures［J］.Yangtze River，1999，(12):8 － 9，12.(in Chinese))

［2］舒荣龙，陈桂馥，杜宗伟.提高三峡－葛洲坝两坝间通航能力试验研究［J］.人民长江，2005，(7):31－33，72.(SHU Rong-long，CHEN Gui-fu，DU Zong-wei.Experiment Study to Improve the Ability of Navigable Flow Conditions Between TGD and Gezhouba Dam［J］.Yangtze River，2005，(7):31 －33，72.(in Chinese))

［3］陈桂馥，文 岑，赵世强.三峡电站汛期调峰对两坝间河段通航条件影响的研究［J］.水运工程，2004，(5):52 －55.(CHEN Gui-fu，WEN Cen，ZHAO Shi-qiang.Influence of Peak Modulation of Three Gorges Power Station in Flood Season on the Navigation Conditions of the Reach Between the Two Dams［J］.Port＆ Waterway Engineering，2004，(5):52 －55.(in Chinese))

［4］丁道扬，吴时强.三维宽浅河道水流数学模型研究［J］.中国工程科学，2010，12(2):32 －39.(DING Daoyang，WU Shi-qiang.Study on Three-Dimensional Numerical Model for Shallow Water Flow［J］.Engineering Science，2010，12(2):32 －39.(in Chinese))