库水波动下库岸边坡地下水浸润线解析解及误差分析

胡 庆，李 漪，李 恒，胡凯锋，郑德宾

(1.中国地震局地震研究所 地震大地测量重点实验室，武汉 430071;2.武汉地震工程研究院，武汉 430071;3.湖北省电力勘测设计院，武汉 430040)

1 研究背景

库水波动是影响库岸边坡变形破坏最主要的动态因素，库水波动下库岸边坡地下水浸润线的合理计算对库区滑坡稳定性分析和预测预报都有重要意义。

近几十年来，很多学者采用不同方法对边/滑坡地下水渗流问题进行了研究，如文献［1－2］分别用有限元方法研究了降雨和库水波动下边坡地下水渗流场的变化趋势;文献［3］用有限差分法研究了降雨和库水波动联合作用下的滑坡地下水浸润线。数值方法能较好解答复杂初始条件和边界条件下的边/滑坡地下水浸润线问题，但目前还未在工程实际中广泛使用，解析法是比数值法更容易推广应用的实用方法。文献［4－6］基于含水层均质、侧向无限延伸并具水平不透水层，库岸垂直，初始地下水位水平和潜水流为一维流等假定，用解析解法研究了不考虑降雨和蒸发作用时库水位等速变化下的滑坡地下水浸润线。文献［7－10］在上述假定的基础上研究了考虑降雨和蒸发影响时的情况，文献［11］用解析解法研究了库水位呈正弦半波曲线变化时的滑坡地下水浸润线。上述解析解都是基于一定假定并对方程线性化处理后得到的，然而，用解析法计算的边/滑坡地下水浸润线经常与实际情况不符，这主要是因为没有系统地研究各种假定和线性化过程带来的误差并分析其适用条件。

结合前人研究成果，本文基于一定假定建立了不同的库岸边坡地下水渗流数学模型，并求出了库水位呈任意函数波动下的库岸边坡地下水浸润线解析解。通过对比分析不同数学模型的数值解和解析解，研究了库岸边坡垂直处理、潜水运动基本方程线性化处理、假定库水位等速变化、不考虑非饱和渗流和Dupuit假定带来的误差及其规律，从而分析计算库岸边坡地下水浸润线解析法的适用范围。

2 解析解答

2.1 基本假定

由于潜水运动基本方程(即布西涅斯克方程)是一个二阶非齐次偏微分方程，只有通过一定的假定并对方程线性化处理后才能给出浸润线的解析解。本文在建立用于解析解答的数学模型时，有以下基本假定:①含水层均质、各向同性，侧向无限延伸并具有水平隔水层;②潜水流为一维流，不考虑垂直潜水面方向的渗流(dupuit假设);③ 库水波动范围的岸坡垂直;④不考虑非饱和渗流，即岩土介质的渗透性与其含水量无关;⑤由于降雨入渗和蒸发作用下岩土体中水的渗流过程十分复杂，目前的处理方法都有较大的误差［12］，本文不考虑降雨入渗和蒸发情况。

2.2 计算模型

基于上述假设，可建立如图1所示的几何模型(将隔水底板高程定为0 m)。

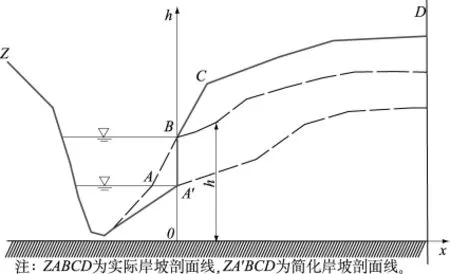
图1 几何模型Fig.1 Geometric model

不考虑降雨入渗和蒸发作用时，潜水一维非稳定运动的基本方程为

式中:潜水面上升时μ为重力给水度，下降时μ为饱和差;t为时间;K为渗透系数;x为位置坐标;h为含水层厚度;H为总水头(隔水底板水平时，h和H相等)。式(1)为一非线性方程，须对其线性化后才能解答，通常采用的线性化方法是用平均含水层厚度hm近似代替h。设水位传导系数a=Khm/μ，有

设 s(x，t)=h(x，t)－ h(x，0)，可得到以含水层厚度变化函数s(x，t)为未知函数的数学模型:

式中f(t)为库水位变动函数，可由库水位－时间曲线经过函数拟合得到。

2.3 解析解

对于上述数学模型，通过对t进行拉普拉斯正变换，解答常微分方程，可得

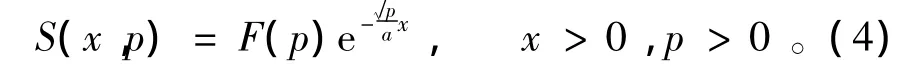
式中:S(x，p)为 s(x，t)关于 t的拉普拉斯变换，F(p)为f(t)关于t的拉普拉斯变换。运用拉普拉斯变换的微分性质和卷积定理对上式进行拉普拉斯逆变换，有

所以有:

若假定库水位等速变化，即f(t)=vt，v为库水变化速度，上升为正，下降为负。则

对上式(7)进行拉普拉斯逆变换，有

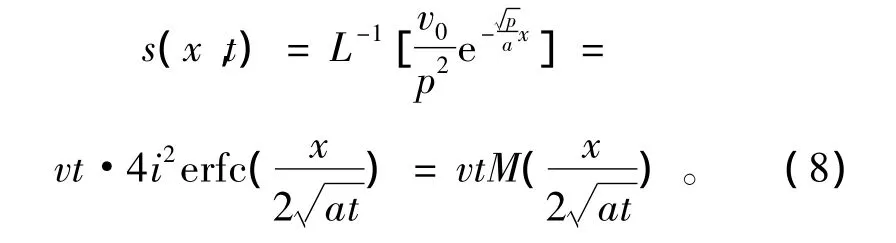
由于M(0)=1，h(x，t)可写成下列统一格式:

其中

M(z)为一特殊函数，可查表获得对应不同z值的函数值［13］，本文对M(z)函数用多项式拟合成如下公式:

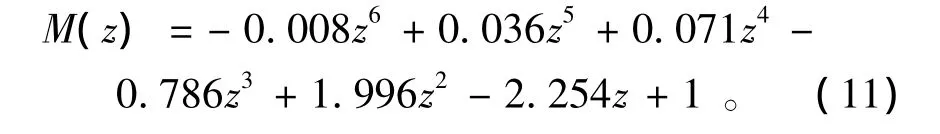
具体解答时，平均含水层厚度hm涉及到渗流结束时的含水层厚度，需迭代才能确定。迭代初值取为h0+1/3H'，h0为初始状态的平均含水层厚度，H'为库水上升或下降的幅度，上升为正，下降为负。用初值代入浸润线计算函数，可得渗流结束时的平均含水层厚度hmn，当hmn与上一步计算结果hmn－1相差足够小时，即可停止迭代计算。

3 误差分析

针对上述建立数学模型时的诸多假定和解答过程中的线性化方法，建立不同的“参照”模型，用有限元程序解答上述“参照”模型并与对应的解析解做比较分析，就可得到各种误差的大小和规律。本文用表示浸润线计算误差，式中(如图2所示):s1为x轴、“参照”模型的浸润线、过2条浸润线交点且平行于h轴的直线三者围成的面积;s2为2条浸润线围成的面积。本文以三峡库区巴东新县城东部的赵树岭滑坡为例进行研究。赵树岭滑坡为一基岩顺层滑坡，滑体南北长约1 000 m，东西宽平均350 m，滑体平均厚度约35 m。滑体主要由块裂、碎裂岩、含泥碎块石及碎块石组成;基岩则以T2b2紫红色粉砂质泥岩、泥质粉砂岩为主。

图2 岸坡垂直处理误差分析Fig.2 Analysis of errors caused by assuming that the reservoir bank is vertical

3.1 岸坡垂直处理带来的误差

解析解答中建立渗流数学模型时假定库水波动范围内的岸坡(图1中的A'B段)坡度为90°。分别建立对应图1中实际剖面和假定剖面的有限元数值模型，取平均渗透系数为0.3 m/d，库水位自34 m高程以1 m/d速度经30 d上升至64 m时的地下水浸润线计算结果如图2所示。

2种数值模型的浸润线计算结果较为接近，P=6.9%。实际岸坡剖面的浸润线要比垂直处理后岸坡的浸润线计算结果更陡一些。如图1所示，岸坡剖面的垂直化处理相当于“削”掉了一部分岸坡岩土体，使得库水在补给岸坡地下水时，其渗流路径更短，这就导致岸坡内地下水浸润线随库水位变化的响应更快。因此，库水上升时，垂直处理后岸坡的浸润线形状相对缓一些。当平均渗透系数取值变大，2种模型计算的浸润线都会越来越接近水平，这时P将逐渐变小至0。

3.2 方程线性化处理带来的误差

有限元法不必对方程线性化处理即可得到浸润线计算结果，因此，通过数值解和解析解的比较就可得到方程线性化处理过程带来的误差。建立k=0.3 m/d，初始水位为20 m高程并以1 m/d速度上升的地下水渗流数学模型。不同库水位波动幅度下的数值解和解析解如图3所示，P值如表1所示。可以看出，随着库水位波动幅度ΔH'的增大，解析解的误差越来越大。若以P=15%为容许误差值，解析解法只适用于ΔH'/hm小于30%的情况。

3.3 假定库水位等速变化带来的误差

本文虽然给出了库水位呈任意函数变化时的库

图3 不同库水位波动幅度下的数值解和解析解Fig.3 Arithmetic and analytic solutions of the equation with different water-level fluctuations

表1 不同库水上升幅度下的P值Table 1 Values of P in the presence of different water level rise

岸边坡浸润线计算公式，但是其结果为函数的变限积分形式，由于实际库水波动曲线比较复杂，很多情况下不能求得便于计算的表达式。因此，常假定库水位呈等速变化，对于实际水位变化复杂的情况可分段考虑，但这就要求每一段都要有一个初始地下水位;因而在实际运用中往往仅考虑水位变化的初始值和末尾值而将其简化为等速变化。经过不同库水变化函数下浸润线计算结果的比较，发现假定库水位等速变化带来的误差有以下特点:当最后时间段库水实际变化速度和假定的平均变化速度相差越大时，误差越大;当渗透系数取值变大时，2种模型计算的浸润线都会越来越接近水平，同时P将逐渐变小至0。

k=0.3 m/d时，图4中2种库水位变化曲线下的浸润线计算结果如图5所示。

对于三峡水库而言，水位变化速度一般不超过1 m/d，且快速蓄水和泄水时，其变化曲线与直线很接近，所以，假定库水位等速变化仅对三峡库区中渗透性很差的库岸边坡浸润线计算有影响。

3.4 不考虑非饱和渗流带来的误差

如果考虑非饱和渗流，则潜水非稳定运动方程中不仅含水层厚度是一个变量，而且渗透系数也是一个变量，其方程如下:

图4 库水位变化曲线Fig.4 Curves of water level fluctuation

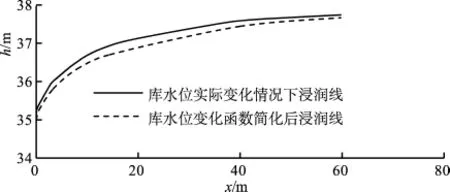
图5 库水位变化函数简化误差分析Fig.5 Errors caused by assuming that the changes in water level is uniform

这是一个非线性化程度更高的方程，解答起来将更加困难。因此，目前的解析解答都没有考虑非饱和渗流，常用一个平均的渗透系数k代替非饱和渗透函数k(θ)。在有限元数值模型中可以用非饱和渗透函数K(θ)=k(k为常数)代表解析解答中不考虑非饱和渗流的情况。通过有限元数值方法解答上述数值模型和实际情况(其非饱和渗透函数按文献［5］取值)下的数值模型。库水位自34 m高程以1 m/d速度经5 d上升至39 m高程时的浸润线计算结果如图6所示，P=17.3%。通过不同的渗透系数取值可以发现，渗透性越好，其误差越小。需要说明的是，不考虑非饱和渗流所引起的误差很大程度上受控于渗流介质的非饱和渗透函数，显然，渗透系数在不同含水量状态下差值越大，误差越大。

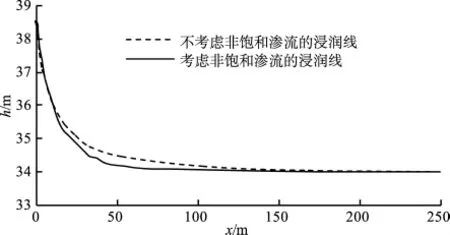
图6 不考虑非饱和渗流的误差分析Fig.6 Analysis of errors caused by the neglect of unsaturated seepage

3.5 Dupuit假设带来的误差

目前广泛应用的非稳定渗流基本方程是基于Dupuit假设的，即假定地下水不发生垂直于浸润线(面)方向的渗流。这种假定在渗出面等水头变化较大的地方附近有一定误差，因为这些地方垂直方向的渗流速度较大。其误差大约为［14］

4 结论

(1)由于潜水非稳定渗流基本方程为二阶非线性偏微分方程，须基于一定假定并对方程线性化处理后才能求得库岸边坡地下水浸润线的解析解，这些假定和线性化处理过程必然带来一定的误差。

(2)库岸垂直处理带来的误差要小于方程线性化处理和不考虑非饱和渗流带来的误差，而且它们都随渗透系数变大而减小;方程的线性化处理带来的误差随库水位波动幅度与含水层厚度之比增大而增大;在三峡库区库水调度情况下，假定库水位等速变化带来的误差可以忽略。

(3)求解库岸边坡地下水浸润线时，解析法有一定的适用范围，针对不同的情况要具体分析。一般而言，解析法适用于库岸边坡岩土结构简单、几何边界规则、渗透性较好且库水波动幅度小于30%含水层厚度时的情况。

［1］吴宏伟，陈守义，庞宇威.雨水入渗对非饱和土坡稳定性影响的参数研究［J］.岩土力学，1999，3(1):1 －14.(WU Hong-wei， CHEN Shou-yi， PANG Yu-wei.Parametric Study of Effects of Rain Infiltration on Unsaturated Slopes［J］.Rock and Soil Mechanics，1999，3(1):1 － 14.(in Chinese))

［2］章广成，唐辉明，胡 斌.非饱和渗流对滑坡稳定性的影响研究［J］.岩土力学，2007，28(5):965 －970.(ZHANG Guang-cheng，TANG Hui-ming，HU Bin.Study of Influence of Unsaturated Seepage on Stability of Landslide［J］.Rock and Soil Mechanics，2007，28(5):965 －970.(in Chinese))

［3］李 晓，张年学，廖秋林，等.库水位涨落与降雨联合作用下滑坡地下水动力场分析［J］.岩石力学与工程学报，2004，23(21):3714 － 3720.(LI Xiao，ZHANG Nianxue，LIAO Qiu-lin，et al.Analysis of Hydrodynamic Field Influenced by Combination of Rainfall and Reservoir Level Fluctuation［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(21):3714 －3720.(in Chinese))

［4］郑颖人，时卫民，孔位学.库水位下降时渗透力及地下水浸润线的计算［J］.岩石力学与工程学报，2004，23(18):3203 － 3210.(ZHENG Ying-ren，SHI Wei-min，KONG Wei-xue.Calculation of Seepage Forces and Phreatic Surface under Drawdown Conditions［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(18):3203 －3210.(in Chinese))

［5］马崇武，刘忠玉，苗天德，等.江河水位升降对堤岸边坡稳定性的影响［J］.兰州大学学报(自然科学版)，2000，36(3):56 － 60.(MA Chong-wu，LIU Zhong-yu，MIAO Tian-de，et al.The Influence of Water Level Changing on the Stability of River Embankment［J］.Journal of Lanzhou University(Natural Sciences)，2000，36(3):56 －60.(in Chinese))

［6］杨红坡，谢新宇，张继发，等.潜水一维非稳态运动的解析理论及应用［J］.水科学进展，2004，15(1):82－86.(YANG Hong-po，XIE Xin-yu，ZHANG Ji-fa，et al.Analytical Solution of One-dimensional Transient Phreatic Flow and Its Application［J］.Advances in Water Science，2004，15(1):82 －86.(in Chinese))

［7］WARRICK A W，WIERENGA P J，PAN L.Downward Water Flow Through Sloping Layers in the Vadose Zone:Analytical Solutions for Diversions［J］.Journal of Hydrology，1997，192:321 －337.

［8］冯文凯，石豫川，柴贺军，等.降雨及库水升降作用下地下水浸润线简化求解［J］.成都理工大学学报(自然科学版)，2006，33(1):90－94.(FENG Wen-kai，SHI Yuchuan，CHAI He-jun，et al.The Simplified Solution of Phreatic Saturation Line under the Actions of Rainfall and Reservoir Water Level Fluctuation［J］.Journal of Chengdu University of Technology(Science＆ Technology Edition)，2006，33(1):90 －94.(in Chinese))

［9］张友谊，胡卸文.库水位等速上升作用下岸坡地下水浸润线的计算［J］.水文地质工程地质，2007，(5):46 －49.(ZHANG You-yi，HU Xie-wen.Calculation of Saturation Line of Groundwater under Reservoir Water Table Uniform Rising［J］.Hydrogeology and Engineering Geology，2007，(5):46 －49.(in Chinese))

［10］吴 琼，唐辉明，王亮清，等.库水位升降联合降雨作用下库岸边坡中的浸润线研究［J］.岩土力学，2009，30(10):3025 －3031.(WU Qiong，TANG Hui-ming，WANG Liang-qing，et al.Analytic Solutions for Phreatic Line in Reservoir Slope with Inclined Impervious Bed under Rainfall and Reservoir Water Level Fluctuation［J］.Rock and Soil Mechanics，2009，30(10):3025 － 3031.(in Chinese))

［11］李相依，晏鄂川.库水位周期性升降作用下滑坡堆积体潜水位计算［J］.四川大学学报(工程科学版)，2007，39(增刊):78 － 81.(LI Xiang-yi，YAN E-chuan.Calculation of Phreatic Surface of Bank Talus under Periodic Fluctuating Reservoir Water Level［J］.Journal of Sichuan University(Engineering Science Edition)，2007，39(Sup.):78 －81.(in Chinese))

［12］朱 伟，陈学东，钟小春.降雨入渗规律的实测与分析［J］.岩土力学，2006，27(11):1873 － 1879.(ZHU Wei，CHEN Xue-dong，ZHONG Xiao-chun.Observation and A-nalysis of Rainfall Infiltration［J］.Rock and Soil Mechanics，2006，27(11):1873 －1879.(in Chinese))

［13］张蔚榛.地下水非稳定渗流计算和地下水资源评价［M］.北京:科学出版社，1983.(ZHANG Wei-zhen.Calculation of Unsteady Groundwater Seepage and Evaluation of Groundwater Resources［M］.Beijing:Science Press，1983.(in Chinese))

［14］薛禹群.地下水动力学［M］.北京:地质出版社，1997.(XUE Yu-qun.Groundwater Dynamics［M］.Beijing:Geological Press，1997.(in Chinese))