随机块体统计分析及其工程支护意义

沈育民，张奇华

(长江科学院 a.长江科创科技发展有限公司;b.水利部岩土力学与工程重点实验室，武汉 430010)

1 研究背景

工程岩体最明显的特征就是因结构面的存在而表现出来的非均质性和各向异性。结构面如节理、断层、岩层层面、剪切带、软弱夹层等，其物理力学性质往往控制着岩体的强度和稳定性，从而决定了岩体的复杂性及其与较完整岩块之间的最大差别。很大程度上，工程岩体的研究往往围绕结构面而展开，或至少应该考虑到结构面的存在所造成的显著影响。

结构面发育特征存在很大的差异。工程岩体质量分级［1］中将岩体结构面分为5级。以水利水电工程为例，Ⅰ级结构面(较大断层)规模大，其对工程的影响是宏观性的，如影响建筑物的总体布置;Ⅱ级结构面相对于建筑物而言也较大。对于硐室和人工边坡影响最大的可能就是Ⅲ—Ⅳ级结构面。结构面切割形成的块体，控制着局部稳定性，并进而可能对较大范围的岩体甚至是整体稳定性造成影响，这一点在硬岩或较低地应力的岩体环境中尤其如此。

Ⅱ，Ⅲ级结构面一般规模较大，能够确定其空间位置及产状，在块体分析中作为定位结构面考虑，切割形成的块体为定位块体或半定位块体;对于岩体中广泛存在的节理裂隙等Ⅳ—Ⅴ级结构面，其产状、长度、空间位置等往往具有随机发育的特点而难以对每条结构面几何性状进行准确描述，切割形成的块体的形态、大小及空间分布具有随机发育的特点。

块体理论(Block Theory)［2］假定岩体结构面为平面、结构体(块体)为刚体，不考虑块体本身的强度破坏，块体运动模式为平动形式，利用几何拓扑方法分析岩体经结构面切割后可能形成的块体类型及失稳模式，进而判断关键块体，分析块体所需的支护力。然而，传统的块体理论中，要求结构面几何及力学性质是确定的，以便对块体的类型、形态特征及稳定性进行分析，因此需要将随机问题简化为确定性问题进行处理。

为了研究随机结构面切割形成的块体问题，发展有随机块体分析方法［3－10］。随机块体分析主要包括2方面内容:

(1)随机块体几何分析。在随机结构面网络模拟基础上，采用块体理论和几何学分析方法，搜索出结构面网络中的三维随机块体，计算随机块体的几何特征参数。

(2)随机块体统计分析［10］。对随机块体大小、形态特征、覆盖率(在临空面上可移动的随机块体所占的面积与临空面面积之比)等进行统计分析，指导随机块体的工程支护。

目前的研究基本上都集中在随机块体分析的第一方面，即对随机块体进行几何搜索［3－9］。其中文献［9－10］对于随机结构面，考虑其产状、延伸长度、间距均为随机分布，通过随机模拟生成三维结构面网络，进而搜索出了三维随机块体，由于在随机结构面网络模拟及块体搜索过程中均未进行简化，搜索得到的块体在统计意义上具有“真实性”。

随机块体的大小(体积、临空面上的面积、埋深)、覆盖率等，可以用于表征块体的发育程度及其对工程稳定的危害性。研究随机块体的大小、覆盖率等的统计分布特征，及其受结构面迹长、间距等的影响，有利于对随机块体的分布规律进行深入认识和研究。

关于随机块体分布规律的研究非常少见。文献［4］在二维上根据结构面分布函数讨论了形成块体的可能性;文献［11］通过概率分析方法讨论了随机节理面形成交点的可能性;Goodman在其关于块体理论的讲座［12］中指出了随机块体分析的工程意义，但未提及随机块体统计分析，以及统计分析对于块体支护分析的重要意义。文献［13］较详细讨论了结构面几何参数的统计分布规律。

随机块体几何分析，可以在三维结构面网络模拟的基础上得到统计意义上的真实三维随机块体。在此基础上，通过随机块体统计分析，可以对随机块体几何特征及发育程度进行定量分析评价，为随机块体稳定及系统支护提供更合理的分析工具。本文在随机块体几何搜索的基础上，对随机块体大小及平均大小等几何特征参数的统计分布规律进行研究，并对随机块体统计分析结果在支护分析中的意义进行探讨。

2 随机块体大小的分布特征

随机块体几何分析及统计分析需要在结构面网络模拟基础上进行。根据成组节理的一般分布规律，假定节理位置在空间上服从均匀分布;由于同组结构面的产状变化对随机块体的统计分布规律没有什么影响，因此取为均值且不变;迹长、间距服从负指数分布，在模拟中取不同的均值，从而对比分析其对统计分布规律的影响。基本模拟参数见表1。临空面产状为208°∠90°。

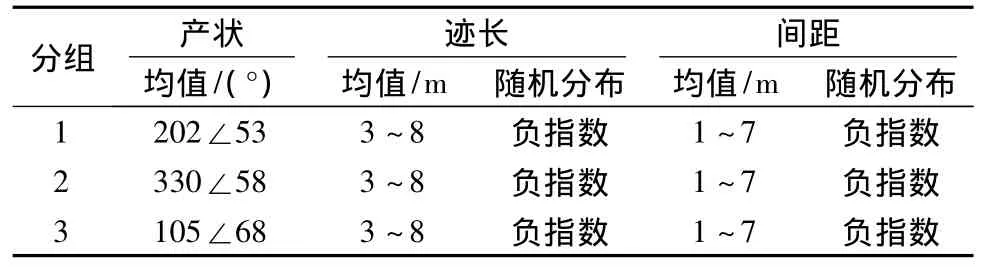
表1 岩体节理网络模拟参数Table 1 Parameters of rock block network simulation

由于节理位置在空间上满足均匀分布，因此搜索出来的随机块体在空间上也满足均匀分布。

对块体的体积、临空面上的面积、埋深进行随机分布规律研究。在考虑3组结构面加临空面切割形成的四面体问题中，由于这三者之间存在几何运算关系，因此分布规律相同。这样，只需对临空面上的面积进行研究。以后叙述中，若非特别说明，块体的面积一般指块体位于临空面上的面积。

节理锥011在临空面切割下可形成可移动块体(通过块体理论中的全空间赤平投影很容易得出这个结论)。当结构面迹长取6.5 m，间距取2.0 m时，一次随机模拟得到结构面网络及在此基础上搜索获得的三维随机块体如图1(a)所示，相应的块体面积分布如图2(a)所示。不同模拟时，得到的结构面网络不同，进行另一次模拟时得到结构面网络及三维随机块体如图1(b)所示，相应的块体面积分布如图2(b)所示。当结构面迹长取6.5 m，间距取4.0 m时，一次模拟得到结构面网络及三维随机块体如图1(c)所示，相应的块体面积分布如图2(c)所示。

图1 结构面网络在临空面上的迹线及搜索得到随机块体Fig.1 The trace lines of discontinuity network on free face and the searched stochastic block

图2结果表明，块体面积的分布形式为负指数分布，即面积越小的块体数量越多。因此可以采用负指数分布刻画块体面积(包括块体的各种尺寸，如块体体积、埋深等)的统计分布特征。这种规律其实可以从图2中直观地看出来。事实上，结构面切割形成块体时，若块体的体积越小，则结构面在开挖面上越容易形成封闭区域，在岩体内部的延伸也越容易将块体切穿，因此形成块体的几率明显越大。大块体区域中包含较多小块体的现象，就是很好的证明。

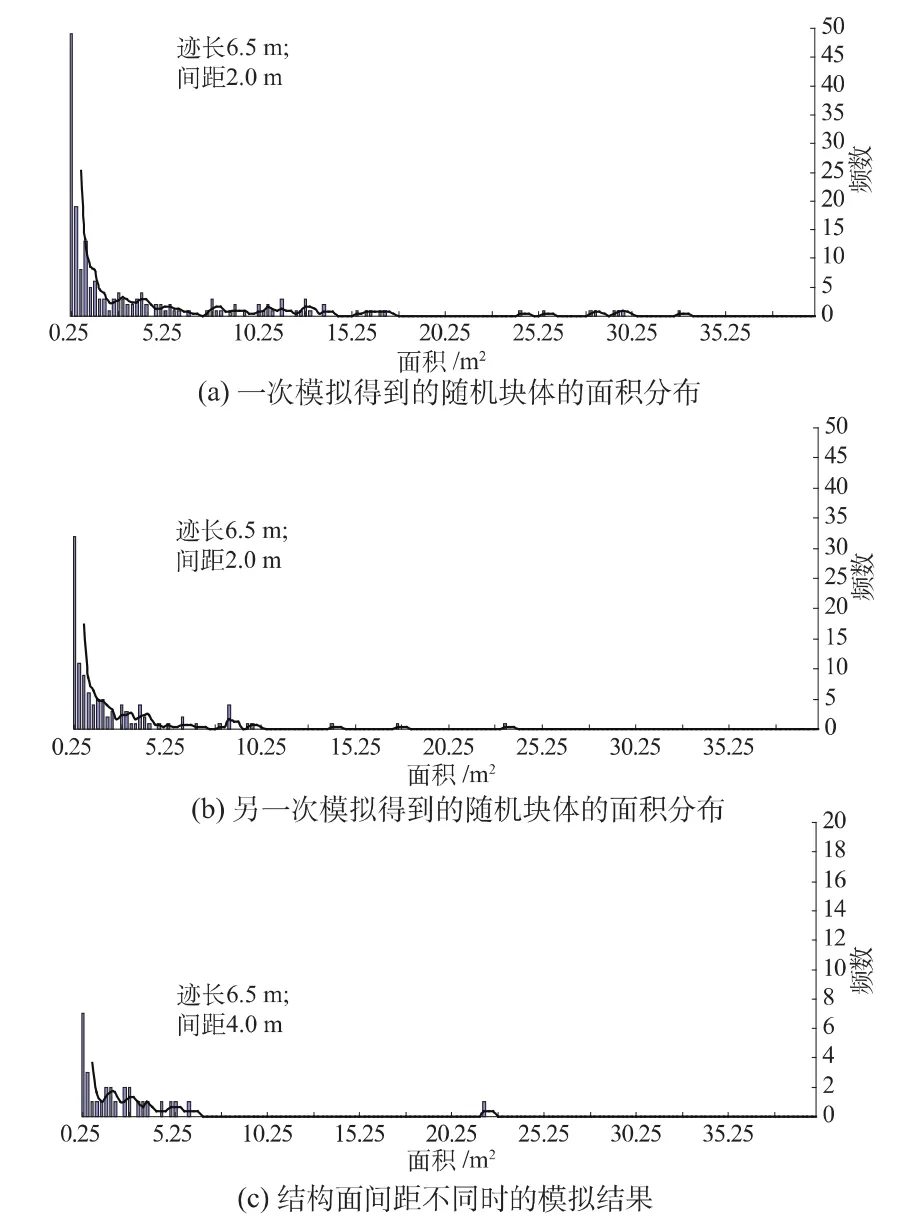
图2 开挖面上块体面积的统计分布Fig.2 Statistical distribution of block area on the excavation plane

3 随机块体平均大小的分布规律

不同模拟样本得到的块体分布不同。同时，块体大小的分布特征也不同，相应的块体平均大小也有不同，如图1(a)至图1(c)所示。因此，我们可以通过成百上千次模拟，研究块体平均大小的分布规律，以更深刻地获得块体大小分布特征的总体规律。

块体大小满足负指数分布，其均值(即块体的平均大小)是密度分布函数的唯一参数，掌握均值的分布规律，有利于深入了解块体大小的分布规律。

在临空面产状与结构面产状分布特征确定的情况下，影响块体大小的因素主要有2方面:结构面间距和迹长。

3.1 间距影响

迹长相同而间距不同时，多次模拟得到的块体平均面积的统计直方图如图3。各算例中，结构面迹长取6.5 m不变，间距在2.0 ～5.0 m变化，模拟次数均为50次。

从图3可以看出，块体的平均面积分布特征可用Γ分布拟合。当然，根据统计直方图形特点假设其满足某种统计分布，需要进行检验，如采用χ2检验，在此从略。

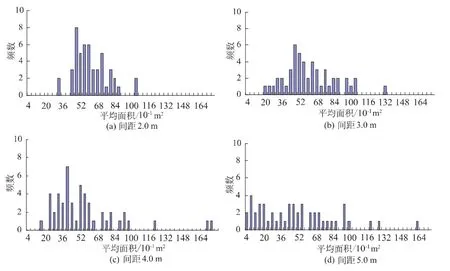
图3 不同间距时块体平均面积的分布Fig.3 Distribution of average area of block in the presence of different spacing between discontinuities

Γ分布的密度函数为

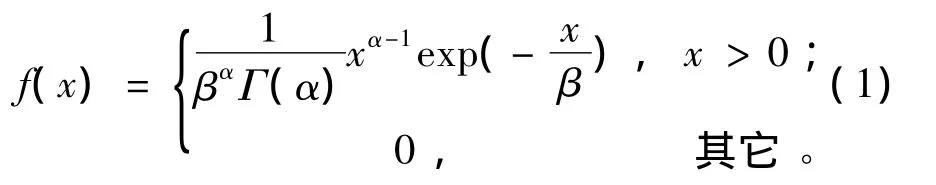
其中α，β为函数参数。

均值、方差分别为:

Γ分布的密度函数如图4所示。当横坐标x＜0时，函数值为0，并且当α较小(＜2)时，密度函数为单调减，随着x增大而急剧减小，类似负指数函数;当α较大时，密度函数呈非对称向左倾斜，函数曲线先升后降，并且，α越大时曲线峰值越小，峰值位置右移，增大和衰减速度越慢。

图3各算例中，样本均值和样本标准差，以及分布的参数α，β见表2。从表2可以看出，当节理间距从2.0～5.0 m取不同值时，Γ分布的参数α明显减小，而β增大，规律性明显。

图4 Γ分布函数特征曲线Fig.4 Characteristic curves of Γ distribution

节理间距变大时，块体的数量明显减少。从表2可知，节理间距变大时，块体平均面积的均值有所减小，标准差增大(即每次模拟得到的块体平均面积越离散)。

表2 不同间距时块体平均面积统计参数估计Table 2 Estimation of statistical parameters of block’s average area in the presence of different spacing between discontinuities

3.2 迹长影响

间距相同而迹长不同时，块体平均面积的统计直方图如图5所示。各算例的间距均为3.0 m，迹长为3.0～8.0 m，模拟次数为50次。相应地，图中各算例的均值、标准差的估计见表3。

图5 不同迹长时块体平均面积的分布Fig.5 Distribution of block’s average area in the presence of different trace length

表3 不同迹长时块体平均面积统计参数估计Table 3 Estimation of statistical parameters of block’s average area in the presence of different trace length

图5也表明，块体的平均面积统计分布可用Γ分布拟合。从表3可知，节理迹长从3.0～8.0 m取不同值时，块体平均面积的均值变大，从1.75 m2增大到8.13 m2，标准差也越大。并且结构面迹长变大时，块体的数量明显增多。

节理迹长变大时，Γ分布的参数α明显增大，而β有所减小，规律性明显。从函数参数变化说明，节理迹长变大与节理间距变小对块体的分布规律的影响相似。

4 基于统计分析的块体支护分析

百色水利枢纽位于郁江上游右江河段，是一座以防洪为主，兼有发电、灌溉、航运等综合效益的大型水利枢纽。地下厂房布置于左坝肩弱～微风化辉绿岩岩体内。厂房洞呈城门洞形，最大跨度20.7 m，最大高度49 m。岩体发育的结构面如表4所示。

表4 百色水利枢纽地下厂房结构面发育情况Table 4 Development of discontinuities of the underground powerhouse of Baise hydrojunction

结构面网络的Monte-Carlo法模拟中，结构面产状满足正态分布，迹长和间距满足负指数分布。

根据块体理论中的全空间赤平投影，节理锥011在厂房下游边墙可以形成可动块体，滑动模式为单面滑动。某次裂隙网络模拟及搜索得到的块体如图6所示，得到块体覆盖率为15.8%。由于块体数量较多，覆盖率较大，因此采用喷锚进行系统支护是必须的。但是由于块体的出现、大小分布等是随机分布的，因此需要进行随机块体搜索及统计分布规律研究，并在此基础上进行块体支护问题分析。

图6 地下厂房搜索得到的随机块体Fig.6 The searched stochastic blocks of the underground powerhouse

随机块体的体积、面积及埋深的统计分布规律对于块体系统支护的设计至关重要。这些是传统块体理论无法实现的。

块体尺寸直接影响锚固力、锚杆间距及长度。由于小块体总是多于大块体，并且小块体能够通过一般的锚杆喷射混凝土进行支护，因此需要在设计中重点关注的是大块体。根据以上结果，块体越大，其出现的可能性越小，然而，块体越大越危险，且支护代价越大。当块体的出现是随机形式的，就应该以可靠度而不是确定性的思想去研究块体支护设计问题。

只研究下游边墙形成的块体支护问题。通过400次模拟，得到块体平均面积与覆盖率的分布如图7、图8所示。块体平均大小、平均埋深及平均体积的均值与方差列于表5中。

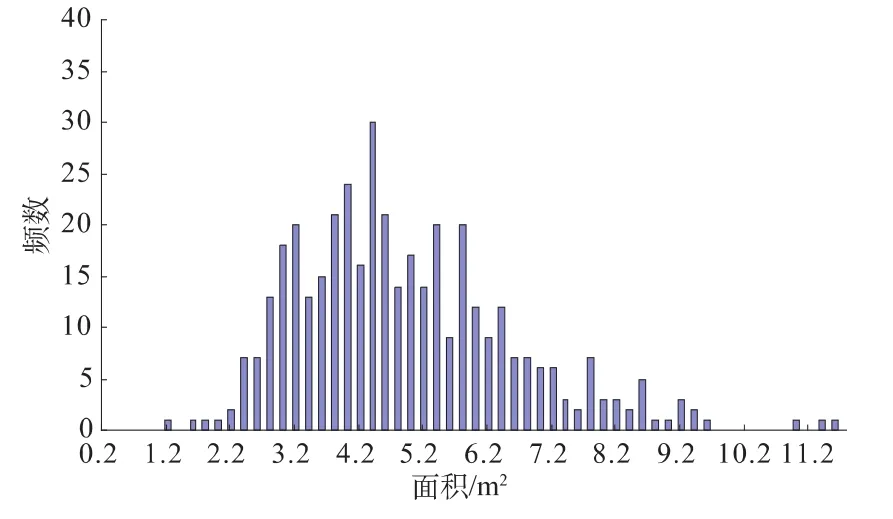
图7 位于上游边墙的随机块体平均大小的分布Fig.7 Distribution of the average size of stochastic block of the upstream sidewall

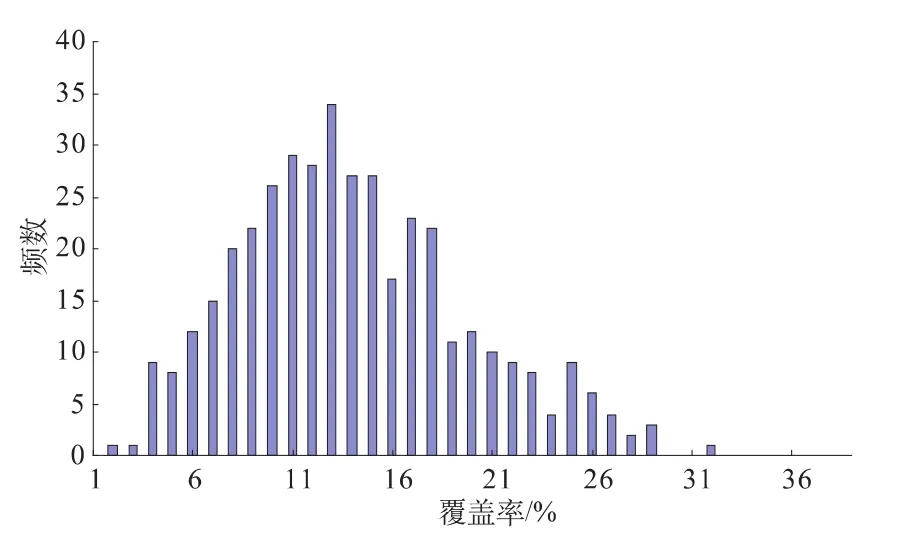
图8 位于上游边墙的随机块体覆盖率分布Fig.8 Distribution of the coverage ratio of stochastic block of the upstream sidewall

表5 有关块体尺寸的统计参数分布Table 5 Statistical parameter distribution of block size

根据以上研究结果，块体尺寸(包括块体位于开挖面上的面积、块体埋深及块体体积)满足负指数分布规律。如表5所示，平均埋深为1.07 m时，块体埋深的密度函数可以表达为

块体体积的密度函数可以表达为

式(3)可以用作确定锚杆的长度，锚杆长度需超过块体埋深一定长度(如1 m)才是有效的锚固参数。通过该式可以计算得到块体埋深分别大于3，4，5，6 m 时的概率分别为6.05%，2.38%，0.93%和0.37%。如果在设计中接受2.38%或0.93%块体埋深超过4 m或5 m，并且考虑锚杆长度超过块体埋深1 m，这样岩体锚杆长度就应该是5～6 m。

式(4)表示的块体体积分布特征与锚固支护力计算，块体面积分布特征与锚杆间距确定有关。具体讨论在此从略。

5 结论

随机块体几何分析，可以在三维结构面网络模拟的基础上得到统计意义上真实的三维随机块体;在此基础上，通过随机块体统计分析，可以对随机块体几何特征及发育程度进行定量分析评价，为随机块体稳定及系统支护提供了更合理的分析工具。本文在随机块体搜索结果基础上，讨论了随机块体统计分析问题。得到以下认识和结论:

(1)为了深入认识随机块体发育特征，定量估计块体危害性，本文对随机块体大小及平均大小等的统计分布规律进行了研究。结果表明块体大小满足负指数分布规律，块体平均大小及覆盖率满足Γ分布。

(2)以百色地下厂房为例，讨论了根据块体统计分布规律进行支护设计的思路和方法。根据块体埋深的分布规律，通过可靠度思想，可以确定锚杆长度;根据块体平均体积分布及块体面积分布特征，可以对块体锚固支护力进行设计。

［1］GB50218—94，工程岩体分级标准［S］.北京:中国计划出版社，1994.(GB50218—94，Standard of Classification of Engineering Rock［S］.Beijing:China Planning Press，1994.(in Chinese))

［2］GOODMAN R E，SHI G H.Block Theory and Its Application to Rock Engineering［M］.Englewood Cliffs，New Jersey:Prentice-Hall Inc.1985.

［3］SHAPIRO A，DELPORT J L.Statistical Analysis of Jointed Rock Data［J］.International Journal of Rock Mechanics and Mining Sciences，1991，28(5):375 －382.

［4］MAULDON M.Key Block Probabilities and Size Distri-butions:A First Model for Impersistent 2-D Fractures［J］.International Journal of Rock Mechanics and Mining Sciences，1995，32(6):575－583.

［5］KUSZMAUL J S.Estimating Key Block Sizes in Underground Excavations:Accounting for Joint Set Spacing［J］.International Journal of Rock Mechanics and Mining Sciences，1999，(36):217 －232.

［6］邬爱清，任 放，郭 玉.节理岩体开挖面上块体随机分布及锚固方式研究［J］.长江科学院院报，1991，8(4):27 －34.(WU Ai-qing，REN Fang，GUO Yu.A Study on Block Random Distribution and Anchor Design for Joint Rock Excavation［J］.Journal of Yangtze River Scientific Research Institute，1991，8(4):27 －34.(in Chinese))

［7］邬爱清，周火明，任 放.岩体三维网络模拟技术及其在三峡工程中的应用［J］.长江科学院院报，1998，15(6):15 －18.(WU Ai-qing，ZHOU Huo-ming，REN Fang.Research on 3-D Rock Joint Network Simulation Techniques and Its Application to TGP［J］.Journal of Yangtze River Scientific Research Institute，1998，15(6):15 －18.(in Chinese))

［8］陈剑平，卢 波，王良奎，等.复杂不稳定块体的自动搜索及其失稳方式判断——基于随机不连续面三维网络模型［J］.岩石力学与工程学报，2003，22(7):1126 －1131.(CHEN Jian-ping，LU Bo，WANG Liangkui，et al.Automatic Search for Complex Unstable Rock Blocks and the Judgment of Instability Mode:Based on 3D Network Simulation of Random Fractures［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22(7):1126 －1131.(in Chinese))

［9］邬爱清，张奇华.岩石块体理论中三维随机块体几何搜索［J］.水利学报，2005，36(4):426－432.(WU Ai-qing，ZHANG Qi-hua.Geometric Identification of Stochastic Block in Block Theory［J］.Journal of Hydraulic Engineering，2005，36(4):426 －432.(in Chinese))

［10］张奇华.岩体块体理论的应用基础研究［M］.武汉:湖北科学技术出版社，2010.(ZHANG Qi-hua.Basic Research on the Application of Rock Block Theory［M］.Wuhan:Hubei Science and Technology Press，2010.(in Chinese))

［11］HATZOR Y H，FEINTUCH A.The Joint Intersection Probability［J］.International Journal of Rock Mechanics and Mining Sciences，2005，42(4):531 －541.

［12］GOODMAN R E.Thirty-fifth Rankine Lecture:Block Theory and Its Application［J］.Geotechnique，1995，45(3):383－423.

［13］KULATILAKEPHSW，WATHUGALADN，STEPHANSSON O.Joint Network Modeling with A Validation Exercise in Stripa Mine，Sweden［J］.International Journal of Rock Mechanics and Mining Sciences，1993，30(5):503－526.