风电系统电压稳定性的Hopf分岔控制仿真
刘继广, 王海洋,, 钟利军, 刘英旋, 李 季, 马幼捷
(1. 白城师范学院 机械工程学院, 吉林 白城 137000;2. 天津理工大学 天津市复杂系统控制理论及应用重点实验室, 天津 300384)
风电具有很强的不确定性和随机性, 大型风电场并网接入将改变系统原有的潮流和网损分布, 从而不同程度地影响接入区域电网的电压稳定性[1]. 风电系统是一个高度非线性动力系统, 电压失稳的外在表现是幅值振荡失稳或瞬间大幅跌落, 分岔是其中的一个主要原因, Hopf分岔是电力系统最常见的分岔现象之一[2]. 分岔控制是通过设计控制器或相应算法改变系统的分岔特性, 进而获得系统的预期动态行为延迟或消除系统Hopf分岔. 分岔控制方法目前主要有线性和非线性反馈、 Washout滤波器方法、 标准型理论方法及频域分析和逼近方法等. 分岔控制的目的是消除或转移系统原有的分岔点, 稳定分岔周期轨道, 引入新的分岔, 改变极限环的幅值等.
目前, 电力系统的Hopf分岔控制研究取得了一些成果, 例如: 文献[3]提出了基于高通滤波器技术的电力系统Hopf分岔控制, 消除了系统存在的Hopf 分岔点, 增大了系统运行的稳定域; 文献[4]基于不变项和规范型给出了电力系统分岔现象的线性和非线性控制的数学分析, 但未给出方法的有效性证明; 文献[5]提出一种以系统负荷为参数的多机电力系统Hopf分岔在线控制方法, 以避免发生Hopf分岔; 文献[6-7]结合参数稳定域的概念, 分别提出了提高电力系统大扰动稳定性和小扰动稳定性的最优分岔控制策略, 保证了系统的稳定性.
本文考虑风电系统的Hopf分岔控制问题, 计算了Hopf分岔点, 分析了无功功率对Hopf分岔点的影响, 并研究了静止无功补偿器SVC对延迟风电系统Hopf分岔的控制作用, 提出利用线性反馈方法消除风电系统的Hopf分岔. 数值仿真实验验证了理论分析结果.
1 Hopf分岔理论及稳定性
考虑非线性动力系统:
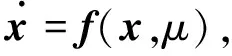
(1)
其中:x∈Rn表示状态变量;μ∈J⊂R表示可变化的系统参数;f: Rn×J→ Rn为唯一的光滑非线性映射. 在平衡点处展开式(1), 有
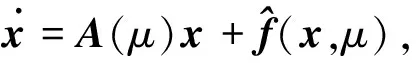
(2)
其中A(μ)为式(1)在点(x0,μ)处的Jacobian矩阵. 当μ连续变化时, 式(1)可从一种响应突然跳变为另一种响应, 这种现象称为分岔.如果A的特征根为一对共轭纯虚根λ(μc)=α(μc)±jωc(μc), 即α(μc)=0, 且横截条件α′(μc)≠0, 则式(1)从Lyapunov意义下的稳定性突然跳变为振荡, 进而系统维持周期性的振荡或振幅不断增大而导致最终失稳, 这种分岔称为Hopf分岔.
2 Hopf分岔的解析算法
当系统发生Hopf分岔后, 可通过求解分岔点附近的曲率系数正负判断发生分岔的类型[8]. 本文利用解析算法求解系统(1)的曲率系数β, 式中变量含义参见文献[8].
先在分岔点处, 计算式(1)的Jacobian矩阵A的特征值为λi(i=1,2,…,n), 将特征值根据Re(λ1)≥Re(λ2)≥…≥Re(λn)进行排序, 然后进行变量代换X=X*+UY(X*是系统的平衡点), 可得Y=f(Y), 当有n-2个实根和一对共轭复根时,U=(Re(V1),-Im(V1),r3,…,rn), 其中:V1表示λ1(μc)=jω0时的A(μc)特征向量;r3,…,rn表示μ=μc时对应于λ3,…,λn的一组特征向量. 如果特征根复根与实根数目不相同, 则U也具有上述形成规律. 曲率系数β的计算公式为
(3)
其中:
3 算例分析
典型含SVC的风电系统模型如图1所示. 该模型由两个发电机和一个风电场组成, G1为无穷大电源, G2为2阶经典同步发电机模型, 风电场采用动态WALVE负荷等值的异步发电机[9-10], SVC安装于风电场异步发电机的等值机端[8].
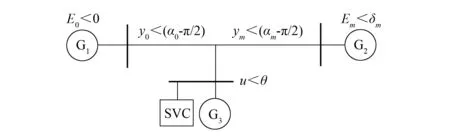
图1 风电系统模型Fig.1 Model of wind power system
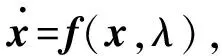
3.1 无功功率对风电系统Hopf分岔的影响
分岔与系统的参数变化关系密切, 当参数发生变化时, 系统将可能失去结构稳定性[11]. 异步发电机吸收的无功功率将在很大程度上影响风电场的稳定运行, 因此, 本文先基于延拓算法, 以风电场吸收的无功功率作为分岔参数进行电压稳定性研究.
图2为风电场的端电压u随无功功率Q1变化而发生分岔的曲线, 当异步风力发电机输出的有功功率逐渐增加时, 其吸收的无功功率q会同时逐渐增加. 由图2可见, 无功功率的增加会导致风电场的端电压u下降, 当系统接近于极限点(limit point, LP)前, 即q=1.499 884时, 系统电压u=0.908 584, 风电系统发生Hopf分岔, 根据本文给出的解析算法, 可求得此时风电系统特征根为一对共轭虚根λ(μc)=±j7.324 8, 系统的曲率系数β=0.031 5. 由Hopf分岔理论, 此时系统发生亚临界分岔. 当风电系统发生亚临界Hopf分岔时, 在分岔点附近, 将会由Lyapunov意义的渐近稳定性跳变到不稳定的非线性振荡, 故风电场吸收的无功功率将影响系统的电压稳定性.
3.2 SVC对风电系统Hopf分岔的影响
图3为加装静止无功补偿器SVC(Kr=1.5,Tr=0.02)后风电场端电压的Hopf分岔曲线. 通过对比图2可知, 加装SVC后, 提高了风电系统的电压水平, 增加了发生Hopf分岔对应的H1点的无功功率(q=11.531 989), 且H1点逼近于LP点. 仿真结果表明, 静止无功补偿器SVC通过补偿风电场所吸收的无功功率, 延迟了Hopf分岔点, 有效提高了系统的电压稳定运行域, 但SVC不能消除Hopf分岔点, 使系统安全运行在极限点前.

图2 q对无SVC风电系统Hopf分岔的影响Fig.2 Effect of q on Hopf bifurcation of a wind power system without SVC
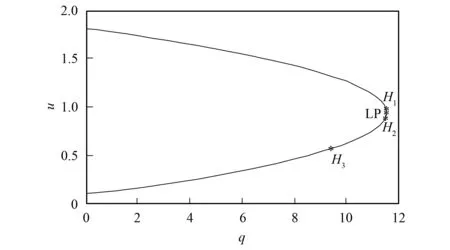
图3 q对加装SVC风电系统Hopf分岔的影响Fig.3 Effect of q on Hopf bifurcation of a wind power system with SVC
3.3 风电系统Hopf分岔的线性反馈控制
线性反馈控制是非常有效的分岔控制方法, 可应用于高维系统及多种分岔现象的控制[12]. 本文针对风电系统的亚临界Hopf分岔, 采用线性反馈控制器进行控制.
对式(1)的线性化系统(2)施加状态反馈控制, 则受控的线性系统为
x=A(μ)x+Bu,
(4)
其中:B∈Rn×n是待定的常数矩阵;u∈Rn是控制向量,
u=-k(x-x0),
(5)
k∈Rn×n表示待定的常数矩阵, 可通过闭环系统(4)的x=A(μ)x-Bk(x-x0)在平衡点处的Jacobian矩阵所选定特征值求取.
对于上述风电系统
x=(δ,ω,θ,u,b)T,f=(f1,f2,…,fn)T.
(6)
(7)
其中k=(kij)为反馈增益矩阵, 可有n2个元素作为控制参数. 可取对角阵
(8)
作为反馈增益矩阵, 当kii都取正值而绝对值又足够大时, 目标态达到稳定, 有
反馈控制可针对少数变量甚至单个变量, 通过参数的合适选择, 即可达到通过单一变量稳定目标态, 甚至控制分岔的目标. 本文取

(9)
可使系统(3)的主导极点远离虚轴, 其他的极点为远离主导极点的负实数, 不对闭环系统产生影响, 消除了Hopf分岔. 当原风电系统的运行点受负荷的小扰动而偏离平衡点时, 即可在反馈控制器作用下快速回到平衡点.
图4为在不改变系统(6) 平衡点的前提下, 采用上述线性状态反馈控制的Hopf分岔曲线. 显然加入反馈控制后, 系统的Hopf分岔点被消除, 但该反馈不能为系统提供无功功率, 所以风电场的电压水平并未得到提高. 图5为含SVC风电系统Hopf分岔的线性变量反馈控制曲线. 由图5可见, Hopf分岔点被消除的同时, 由于SVC能够补偿风电场吸收的无功功率, 所以电压稳定域得到提高.
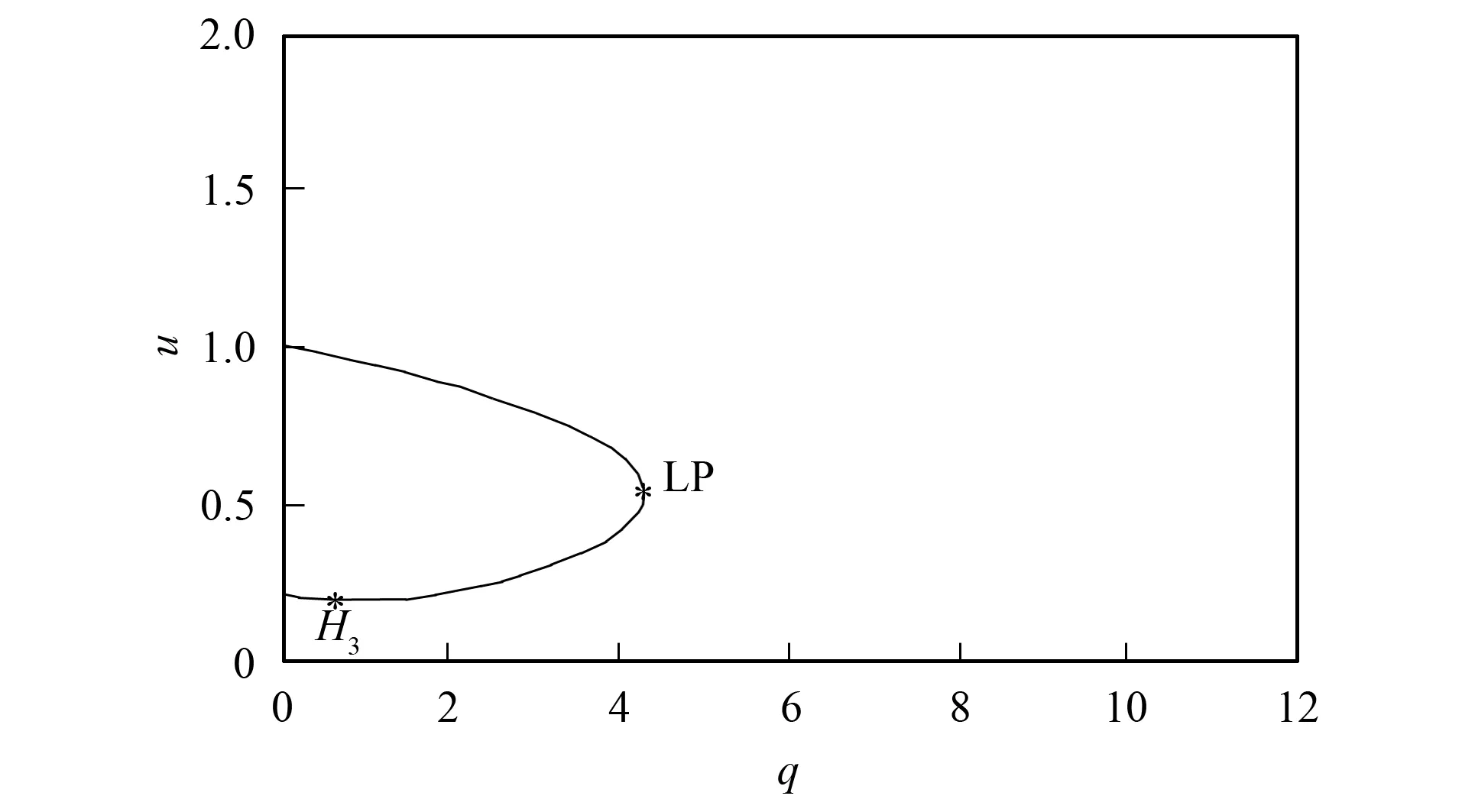
图4 不含SVC风电系统Hopf分岔 的线性变量反馈控制曲线Fig.4 Hopf bifurcation linear feedback control curve of the wind power system without SVC
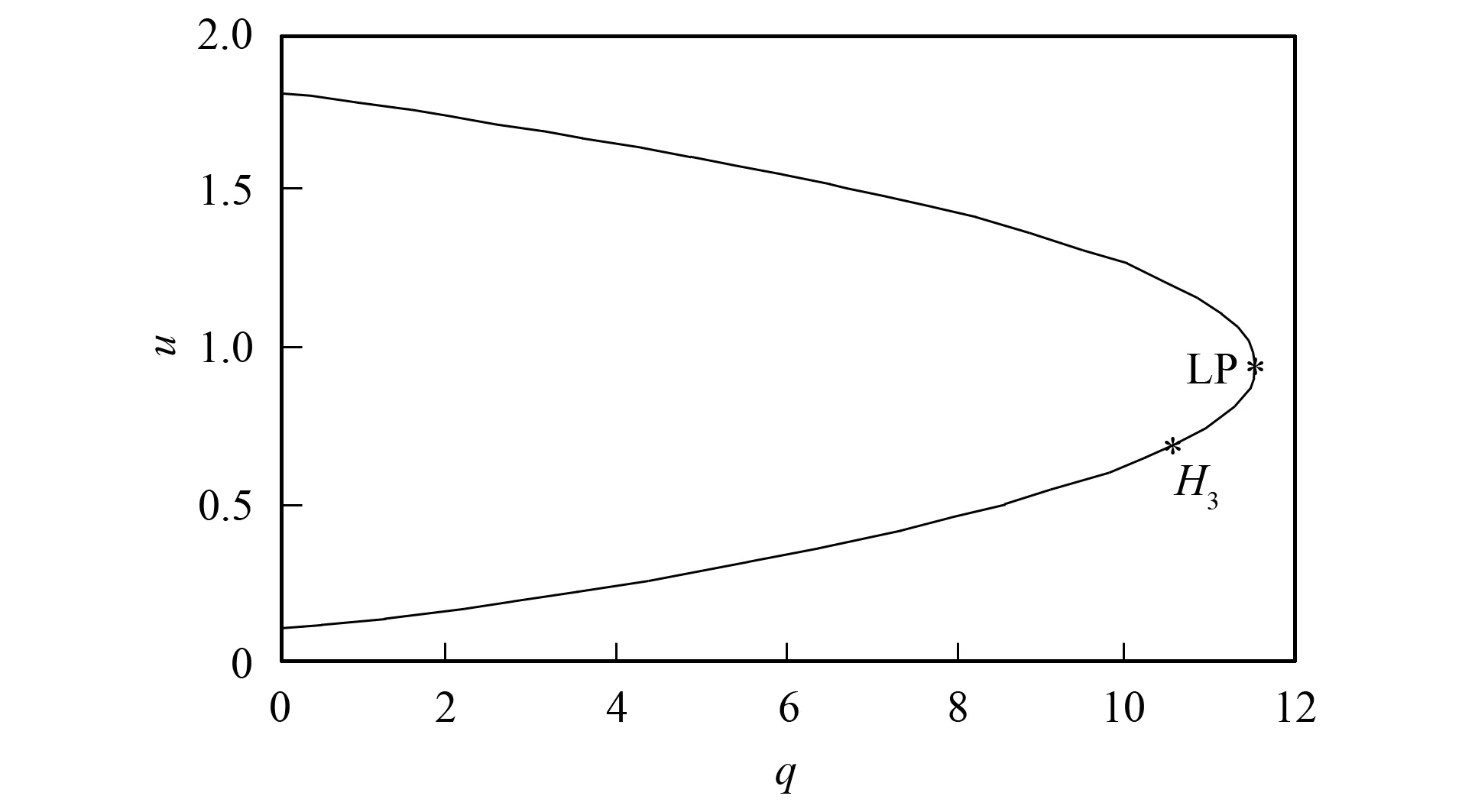
图5 含SVC风电系统Hopf分岔 的线性变量反馈控制曲线Fig.5 Hopf bifurcation linear feedback control curve of the wind power system with SVC
综上可见, 基于异步发电机的风电系统属于非线性动力系统, 具有非线性动力系统独有的分岔现象. 本文通过对风电系统的分岔现象进行分析, 研究了无功功率对风电系统电压稳定性的影响. 结果表明, 采用单个变量的反馈控制方法对含SVC风电系统的Hopf分岔点可进行有效控制, 消除了Hopf分岔点, 防止了电压崩溃, 且易于实现.
[1] Eknath V, Mark O M, Andrew K. A Steady-State Voltage Stability Analysis of Power Systems with High Penetrations of Wind [J]. IEEE Trans on Power Systems, 2010, 25(1): 433-442.
[2] LI Hong-zhong, CHENG Hao-zhong, TENG Le-tian, et al. A Direct Method for Computing Hopf Bifurcation Point in Power System Dynamic Voltage Stability [J]. Proceedings of the CSEE, 2006, 26(8): 28-32. (李宏仲, 程浩忠, 滕乐天, 等. 以简化直接法求解电力系统动态电压稳定分岔点 [J]. 中国电机工程学报, 2006, 26(8): 28-32.)
[3] MA You-jie, LI Xiao-shuang, ZHOU Xue-song. Hopf Bifurcation Control of Power System Based on High-Pass Filter Technology [J]. Power System Technology, 2011, 35(7): 76-80. (马幼捷, 李小双, 周雪松. 基于高通滤波器技术的电力系统霍普分岔控制 [J]. 电网技术, 2011, 35(7): 76-80.)
[4] QIAO Yu, WANG Hong-li, ZHU Zhi-wen. Bifurcation Control of Power Systems [J]. Acta Mechanica Sinica, 2002(34): 380-383. (乔宇, 王洪礼, 竺致文. 电力系统的分岔控制研究 [J]. 力学学报, 2002(34): 380-383.)
[5] WANG Shao-bu, JIANG Quan-yuan, CAO Yi-jia. On-Line Hopf Bifurcation Control in Multi-machine Power System [J]. Automation of Electric Power Systems, 2008, 32(11): 1-5. (王韶部, 江全元, 曹一家. 多机电力系统Hopf分岔的在线控制 [J]. 电力系统自动化, 2008, 32(11): 1-5.)
[6] GU Wei, JIANG Ping, TANG Guo-qing. Optimal Bifurcation Control to Improve Large-Disturbance Stability of Power Systems [J]. Electric Power Automation Equipment, 2007, 27(11): 12-17. (顾伟, 蒋平, 唐国庆. 提高电力系统大扰动稳定性的最优分岔控制策略 [J]. 电力自动化设备, 2007, 27(11): 12-17.)
[7] GU Wei, JIANG Ping, TANG Guo-qing. Optimal Bifurcation Control to Improve Small-Signal Stability of Power Systems [J]. Electric Power Automation Equipment, 2007, 27(10): 29-33. (顾伟, 蒋平, 唐国庆. 提高电力系统小扰动稳定性的最优分岔控制策略 [J]. 电力自动化设备, 2007, 27(10): 29-33.)
[8] DENG Ji-xiang, ZHANG Xin-yu, TONG Jian-dong. Study on Effect of System Parameters for Hopf Bifurcation [J]. Transaction of China Electrotechnical Society, 2007, 22(9): 130-135. (邓集祥, 张新宇, 童建东. 系统参数对Hopf分岔影响的研究 [J]. 电工技术学报, 2007, 22(9): 130-135.)
[9] LI Hui, HAN Li, ZHAO Bin, et al. Effect of Equivalent Models of Wind Turbines on Analysis Results of Transient Stability for Wind Generator Systems [J]. Proceedings of the CSEE, 2008, 28(17): 105-111. (李辉, 韩力, 赵斌, 等. 风电机组等效模型对机组暂态稳定分析结果的影响 [J]. 中国电机工程学报, 2008, 28(17): 105-111.)
[10] Hua O W, Eyad H A, Anan M. Bifurcations, Chaos and Crises in Voltage Collapse of a Model Power System [J]. IEEE Trans on Circuits and Systems-I Fundamental Theory and Applications, 1994, 41(3): 294-302.
[11] Seydel R. Practical Bifurcation and Stability Analysis: from Equilibrium to Chaos [M]. New York: Springer-Verlag, 1994.
[12] WU Zhi-qiang, SUN Li-ming. Hopf Bifurcation Control of the Rossler System Based on Washout Filter Controller [J]. Acta Phys Sin, 2011, 60(5): 1-5. (吴志强, 孙立明. 基于Washout滤波器的Rossler系统Hopf分岔控制 [J]. 物理学报, 2011, 60(5): 1-5.)

