偏 微 分 包 含 的 端 点 问 题

程 毅, 华宏图, 李秋月

(1. 吉林大学 数学研究所, 长春 130012; 2. 空军航空大学 基础部, 长春 130022)

微分包含是非线性分析理论的重要分支, 它与微分方程、 最优控制及最优化等问题紧密相联. 对于微分包含的初值和周期问题, 目前已有很多研究结果[1-6]. 但由于偏微分包含问题较复杂, 因此研究结果相对较少. 文献[7]讨论了一类偏微分包含问题： -Δu∈G(x,u), 利用集值的Kakutani不动点定理, 证明了在凸情形下其边值解的存在性. 进一步, 本文考虑其端点解的存在性.

设RN是N维实的Euclid空间, ‖·‖,‖·‖X分别表示RN空间和Banach空间X空间的范数.Pk(f)c(R)表示实数集 R的所有非空紧(闭)凸子集的全体.

设k为正整数, 函数集合

Wk,p(Ω)={u:Dαu∈Lp(Ω), ∀α≤k}

赋以范数

设Z是度量空间, 则在Pf(Z)上可以定义一个广义度量, 即Hausdorff度量. 设C,E,∈Pf(Z), 定义C,E的Hausdorff度量如下：

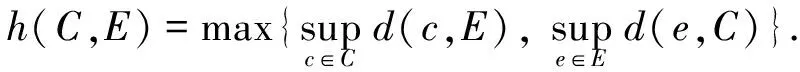
若Z是完备的度量空间, 则(Pk(Z),h)也是完备的度量空间.

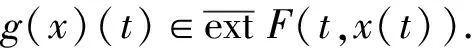
设Ω⊂RN的有界开集其边界光滑, 考虑如下边值问题：

(1)

这里extG(x,u,u)表示集值映射G:Ω×R→2R{Ø}的端点集. 设G满足下列假设条件.

(H) 集值映射G:Ω×R→Pkc(R)使得：

1) (x,u)→G(x,u)是图像可测的；

2) 对几乎所有的x∈Ω, 都有u→G(x,u)是h-连续的；

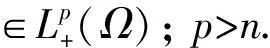
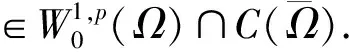
证明: 设问题(1)的解集为Se, 则由文献[7]中解的先验估计知,

Se=sup{‖u‖W2:u∈Se}≤M.

[1] HU Shou-chuan, Papageorgiou N S. Handbook of Multivalued Analysis (Ⅰ): Theory [M]. Dordrecht: Kluwer Academic Publishers, 1997.

[2] XUE Xiao-ping, YU Jin-feng. Periodic Solutions for Semi-linear Evolution Inclusions [J]. J Math Anal Appl, 2007, 331(2): 1246-1262.

[3] XUE Xiao-ping, CHENG Yi. Existence of Periodic Solutions of Nonlinear Evolution Inclusions in Banach Spaces [J]. Nonlinear Analysis: Real World Applications, 2010, 11(1): 459-471.

[4] LI Guo-cheng, XUE Xiao-ping. On the Existence of Periodic Solutions for Differential Inclusions [J]. J Math Anal and Appl, 2002, 276: 168-183.

[5] Cernea A. Continuous Version of Filippov’s Theorem for Fractional Differential Inclusions [J]. Nonlinear Anal, 2010, 72: 204-208.

[6] Alberto Bressan, Giancarlo Facchi. Trajectories of Differential Inclusions with State Constraints [J]. J Differential Equations, 2011, 250: 2267-2281.

[7] CHENG Yi, CONG Fu-zhong. Existence of Solutions for a Class of Partial Differential Inclusions [J]. Journal of Jilin University: Science Edition, 2010, 48(6): 964-967. (程毅, 从福仲. 一类偏微分包含解的存在性 [J]. 吉林大学学报: 理学版, 2010, 48(6): 964-967.)

[8] Tolstonogov A A. Existence and Relaxation Theorems for Extreme Continuous Selectors of Multifunctions with Decomposable Values [J]. Topology and Its Applications, 2008, 155(8): 898-905.