一类非自治二阶哈密顿系统的周期解

吴 越, 安天庆

(河海大学 理学院, 南京 210098)

0 引 言

考虑非自治二阶哈密顿系统

(1)

其中:T>0;F: [0,T]×RN→R满足如下假设：

(H) 对每个x∈RN,F(t,x)关于t可测, 对几乎所有的t∈[0,T],F(t,x)关于x连续可微, 且存在a∈C(R+,R+),b∈L1(0,T;R+), 使得

F(t,x)≤a(x)b(t),F(t,x)≤a(x)b(t),

对所有的x∈RN和a.e.t∈[0,T]成立.

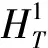
则φ连续可微且弱下半连续[1], 其中

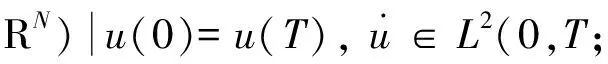
是Hilbert空间, 其上的范数定义为

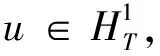
直接计算可得

泛函φ的临界点即为问题(1)的解[1].

目前, 利用临界点理论研究问题(1)周期解的存在性与多重性已有许多结果[1-12]. Mawhin等[1]在F是凸函数的条件下, 利用极小极大化方法证明了问题(1)至少有一个周期解. 对于非凸情形, 文献[2-12]给出了各种合理的限制条件, 例如次可加条件和次二次增长条件等. 除文献[5]外, 目前已有文献多是在条件

(2)

1 主要结果

定理1设F(t,x)=F1(t,x)+F2(x)满足假设(H)及以下条件：

F1(t,x)≤f(t)x+g(t);

(3)

2) 存在常数α∈[0,2)和r>0, 使得对一切x,y∈RN, 有

(F2(x)-F2(y),x-y)≥-r;

(4)

3)

(5)

注1令

定理2设F(t,x)=F1(t,x)+F2(x)满足假设(H)、 定理1中条件1)及以下条件：

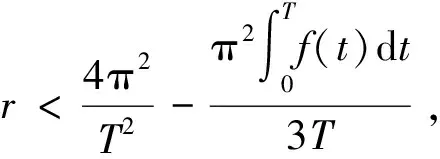
(F2(x)-F2(y),x-y)≥-r;

(6)

2)

(7)

注2令

定理3设F(t,x)=F1(t,x)+F2(x)满足假设(H)、 定理1中条件1),2)及以下条件：

1) 存在β∈[0,2)和C>0, 使得对一切x,y∈RN, 有

(F2(x)-F2(y),x-y)≤C;

(8)

2)

(9)

注3令

其中:h∈L1(0,T;RN);r>0. 此时定理3条件1)中的α=5/3, 定理3成立, 但不满足文献[1-12].

2 定理的证明

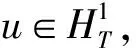
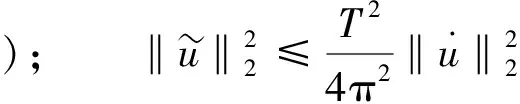
2.1 定理1的证明

(10)

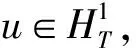
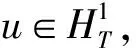
由式(11),(12)可知

2.2 定理2的证明

(14)

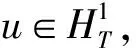
(15)

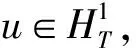
由式(15),(16)可知

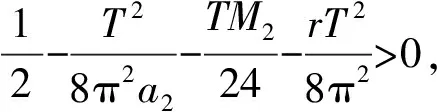
2.3 定理3的证明

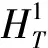
则易知

(18)

与定理1的证法类似, 有

(19)

由式(19)及式(12), 有

其中

(22)

进而

(23)

其中0

由定理3的条件1), 有

由φ(un)的有界性及式(22),(23), 有

φ(u)→∞,u→∞.

(25)

由定理1中条件2)及Sobolev不等式, 有

[1] Mawhin J, Willem M. Critical Point Theory and Hamiltonian Systems [M]. New York: Springer-Verlag, 1989.

[2] Rabinowitz P H. Minimax Methods in Critical Point Theory with Applications to Differential Equantions [M]. Conference Board of the Mathematical Sciences Regional Conference Series in Mathematics Number 65. Providence, RI: American Mathematical Society, 1986.

[3] WU Xing-ping, TANG Chun-lei. Periodic Solutions of a Class of Non-autonomous Second-Order Systems [J]. J of Math Anal and Appl, 1999, 236(2): 227-235.

[4] Aizmahin N, AN Tian-qing. The Existence of Periodic Solutions of Non-autonomous Second-Order Hamiltonian Systems [J]. Nonlinear Analysis: Theory, Methods & Applications, 2011, 74: 4862-4867.

[5] TANG Xian-hua, MENG Qiong. Solutions of a Second-Order Hamiltonian System with Periodic Boundary Conditions [J]. Nonlinear Analysis: Real World Applications, 2010, 11(5): 3722-3733.

[6] YANG Ri-gao. Periodic Solutions of Some Non-autonomous Second Order Hamiltonian Systems [J]. Nonlinear Analysis: Theory, Methods & Applications, 2008, 69(8): 2333-2338.

[7] TANG Chun-lei. Periodic Solutions of Nonautonomous Second Order Systems with Sublinear Nonlinearity [J]. Proc Amer Math Soc, 1998, 126(11): 3263-3270.

[8] MA Jian, TANG Chun-lei. Periodic Solutions for Some Nonautonomous Second-Order Systems [J]. J of Math Anal and Appl, 2002, 275(2): 482-494.

[9] ZHANG Xing-yong, ZHOU Ying-gao. Periodic Solutions of Non-autonomous Second Order Hamiltonian Systems [J]. J of Math Anal and Appl, 2008, 345(2): 929-933.

[10] TANG Chun-lei. Existence and Multiplicity of Periodic Solutions of Non-autonomous Second Order Systems [J]. Nonlinear Analysis: Theory, Methods & Applications, 1998, 32(3): 299-304.

[11] TANG Chun-lei. Periodic Solutions of Non-autonomous Second Order Systems [J]. J of Math Anal and Appl, 1996, 202(2): 465-469.

[12] ZHAO Fu-kun, WU Xian. Periodic Solutions for a Class of Non-autonomous Second Order Systems [J]. J of Math Anal and Appl, 2004, 296(2): 422-434.