非线性扰动薛定谔耦合系统的冲击波解
徐 惠, 许永红, 刘晓伟, 温朝晖
(1. 安徽财经大学 统计与应用数学学院, 安徽 蚌埠 233030; 2. 蚌埠学院 数理系, 安徽 蚌埠 233030)
冲击波理论在量子物理、 光学、 流体力学等领域应用广泛, 目前已有很多研究结果[1-4]. 其中, 使用渐近方法求解冲击波是一种较新的方法, 它改变了以往单纯用数值模拟讨论冲击波的性态, 而是通过解析理论得到冲击波的近似表达式. 其优点在于可以通过渐近表达式进一步用解析运算工具对冲击波性态进行更深入的研究[5-7]. 近年来, 许多渐近方法不断被改进[8-10]. 文献[11-17]应用渐近方法讨论了一类非线性问题. 本文用一种改进的渐近方法讨论一类非线性扰动Schrödinger耦合系统, 并得到了对应冲击波的近似解. 考虑如下非线性扰动Schrödinger耦合系统:
其中:u(x,t),v(x,t)为对应系统的物理场函数;a为正参数;f,g为扰动项, 是在相应的变化范围内充分光滑的有界函数. 系统(1)-(2)描述了一类光导纤维等方面的冲击波传播系统[18]. 本文用一个简单的方法得到了系统(1)-(2)的渐近解.
先考虑如下典型的Schrödinger耦合系统:
引入行波变换ξ=x+ct, 其中c为波速. 利用G′/G方法[18]可得系统(3)-(4)具有如下的精确冲击波解:
其中:σ>0为常数;Ci(i=1,2)为任意常数;
(7)
1 扰动Schrödinger耦合系统的近似解
由于非线性耦合系统(1)-(2)一般不能得到初等函数形式的精确解, 因此为了得到扰动Schrödinger耦合系统(1)-(2)冲击波解的近似表示式, 先引入泛函[6]:
(8)

(9)
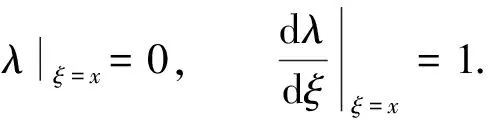
(10)
由式(9),(10), 有解
(11)
于是, 由式(8),(11), 可构造求解u(x,t)的迭代式:
(12)
再由式(2), 可构造求解v(x,t)的迭代式:
(13)
由式(5),(6), 选取初始迭代u0(x,t),v0(x,t)为
(14)
从而, 由式(12),(13)和式(5),(6),(14), 可得系统(1)-(2)的一次近似解:

2 应用实例
为简单, 考虑一个特殊的扰动Schrödinger耦合系统, 其扰动项为f(u,v)=εsinu,g(u,v)=εcosv, 其中ε为小参数. 此时系统(1)-(2)为
由式(5),(6),(14), 选取初始近似u0(x,t),v0(x,t)为
其中B(x,t)由式(7)表示.
由式(12),(13)和式(17),(18), 可得系统(15)-(16)的一次近似解和二次近似解:
继续利用同样的方法可得扰动Schrödinger耦合系统(15)-(16)的更高次近似的冲击波解un app(x,t),vn app(x,t)(n=3,4,…). 也可证明非线性扰动Schrödinger耦合系统(15)-(16)的冲击波解有如下估计式[19]:u(x,t)=un app(x,t)+O(εn+1),v(x,t)=vn app(x,t)+O(εn+1), 0<ε≪1. 因此, 利用本文提出的渐近方法得到的冲击波近似解具有较好的精确度.
综上所述, 由于冲击波理论来源于一类复杂的自然现象, 因此需要简化它为基本模型. 本文利用变分迭代理论用一个简单而有效的方法得到了非线性扰动Schrödinger耦合系统的冲击波渐近解. 由渐近方法求解模型的近似解, 不同于单纯模拟得到的数值解. 由于渐近解具有解析形式的结构, 因此它还可以进行微分、 积分等解析运算, 从而进一步了解相应冲击波解的更深层性态.
[1] Sirendaoreji J S. Auxiliary Equation Method for Solving Nonlinear Partial Differential Equations [J]. Phys Lett A, 2003, 309(5/6): 387-396.
[2] McPhaden M J, ZHANG Dong-xiao. Slowdown of the Meridional Overturning Circulation in the Upper Pacific Ocean [J]. Nature, 2002, 415: 603-608.
[3] PAN Liu-xian, ZUO Wei-ming, YAN Jia-ren. The Theory of the Perturbation for Landau-Ginzburg-Higgs Equation [J]. Acta Phys Sin, 2005, 54(1): 1-5. (潘留仙, 左伟明, 颜家壬. Landau-Ginzburg-Higgs方程的微扰理论 [J]. 物理学报, 2005, 54(1): 1-5.)
[4] FENG Guo-lin, DAI Xing-gang, WANG Ai-hui, et al. On Numerical Predictability in the Chaos System [J]. Acta Phys Sin, 2001, 50(4): 606-611. (封国林, 戴兴刚, 王爱慧, 等. 混沌系统中可预报性的研究 [J]. 物理学报, 2001, 50(4): 606-611.)
[5] LIAO Shi-jun. Beyond Perturbation: Introduction to the Homotopy Analysis Method [M]. New York: CRC Press Co, 2004.
[6] 何吉欢. 工程和科学计算中的近似非线性分析方法 [M]. 郑州: 河南科学技术出版社, 2002.
[7] HE Ji-huan, WU Xu-hong. Construction of Solitary Solution and Compacton-Like Solution by Variational Iteration Method [J]. Chaos Solitions & Fractals, 2006, 29(1): 108-113.
[8] Bartier J P. Global Behavior of Solutions of a Reaction-Diffusion Equation with Gradient Absorption in Unbounded Domains [J]. Asymptotic Anal, 2006, 46(3/4): 325-347.
[9] Libre J, Silva P R, Teixeira M A. Regularization of Discontinuous Vector Fields on R3via Singular Perturbation [J]. J Dyn Differ Equations, 2007, 19(2): 309-331.
[10] Guarguaglini F R, Natalini R. Fast Reaction Limit and Large Time Behavior of Solutions to a Nonlinear Model of Sulphation Phenomena [J]. Commun Partial Differ Equations, 2007, 32(2): 163-189.
[11] XU Hui, CHEN Li-hua, MO Jia-qi. Matched Asymptotic Solution to a Class of Singularly Perturbed Thin Plate Bending Problem [J]. Acta Phys Sin, 2011, 60(10): 100201. (徐惠, 陈丽华, 莫嘉琪. 一类奇摄动薄板弯曲问题的匹配渐近解 [J]. 物理学报, 2011, 60(10): 100201.)
[12] XU Hui, WEN Zhao-hui, MO Jia-qi. Interior Shock Layer Solution with for a Class of Reaction Diffusion Equations [J]. J of Lanzhou University: Natural Sciences, 2010, 46(5): 93-95. (徐惠, 温朝晖, 莫嘉琪. 一类反应扩散方程内部冲击层解 [J]. 兰州大学学报: 自然科学版, 2010, 46(5): 93-95.)
[13] XU Yong-hong, WEN Zhao-hui, XU Hui, et al. Solitary Wave Solution for Physical Model of Disturbed Benjamin Equation [J]. Journal of Jilin University: Science Edition, 2011, 49(4): 659-663. (许永红, 温朝晖, 徐惠, 等. 扰动Benjamin方程物理模型的孤波解 [J]. 吉林大学学报: 理学版, 2011, 49(4): 659-663.)
[14] XU Hui, XU Yong-hong, LIU Xiao-wei. Asymptotic Solution of Differential Equation in the Transmission Wave of a Laser Pulse Amplifier [J]. J of Anhui Normal University: Natural Science, 2010, 33(6): 551-553. (徐惠, 许永红, 刘晓伟. 激光脉冲放大传输波中微分方程的奇摄动渐近解 [J]. 安徽师范大学学报: 自然科学版, 2010, 33(6): 551-553.)
[15] MO Jia-qi. Homotopic Mapping Solving Method for Gain Fluency of a Laser Pulse Amplifier [J]. Science in China: Ser G, 2009, 52(7): 1007-1010.
[16] MO Jia-qi, LIN Su-rong. The Homotopic Mapping Solution for the Solitary Wave for a Generalized Nonlinear Evolution Equation [J]. Chin Phys B, 2009, 18(9): 3628-3631.
[17] MO Jia-qi. Solution of Travelling Wave for Nonlinear Disturbed Long-Wave System [J]. Commun Theor Phys, 2011, 55(3): 387-390.
[18] LI Bang-qing, MA Yu-lan, WANG Cong, et al. Folded Soliton with Periodic Vibration for a Nonlinear Coupled Schrödinger System [J]. Acta Phys Sin, 2011, 60(6): 060203. (李帮庆, 马玉兰, 王聪, 等. 耦合Schrödinger系统的周期振荡折叠孤子 [J]. 物理学报, 2011, 60(6): 060203.)
[19] Barbu L, Morosanu G. Singularly Perturbed Boundary-Value Problems [M]. Basel: Birkhäuser Verlag AG, 2007.

