复合凸优化问题的稳定强对偶
赵 丹,孙祥凯
(1. 重庆工商大学融智学院,重庆 400033;2. 重庆工商大学 数学与统计学院,重庆 400067)
复合凸优化问题(即目标函数是凸函数的复合)应用广泛. 许多最优化问题,如极大极小优化问题、 凸优化问题及目标函数是凸函数和线性算子复合的约束优化问题等都可以作为复合凸优化问题的特例;许多实际应用的最优化问题模型,如位置问题、 交通运输问题和经济学问题等都涉及到复合凸函数[1-5]. 对于复合凸优化问题对偶问题的研究,目前主要借助共轭函数上图的性质引入各种约束品性并用其刻画对偶理论[6-8]. 但上述问题都要求相关函数具有连续性或下半连续性及相关集合具有闭性的假设,且许多实际问题中,常会遇到相关函数不具有连续性或相关集合不具有闭性假设的情形. 目前利用该方法研究无约束优化问题以及无限约束优化问题的对偶问题报道较少[9-10]. 基于此,本文在所考虑函数不一定下半连续或集合不一定闭的情形下,通过引入复合凸优化问题的对偶问题,借助约束品性刻画了其稳定强对偶及强对偶.


对于乘积空间X*×R,本文赋予w(X*,X)和通常的欧氏拓扑的乘积拓扑.


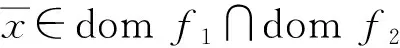
定义1[2]设M⊆X,Z⊆X,若M∩Z=clM∩Z,则称集合M相对于子空间Z是闭的.

所谓稳定强对偶,是指对给定优化问题的目标函数做一个线性扰动后而得到的新问题的强对偶. 对于问题(P),它的最优值记为val(P).
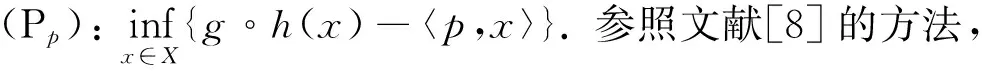
由文献[6]中命题3.1可得下述弱对偶.
定理1(稳定弱对偶) 问题(Pp)和(Dp)之间的弱对偶成立,即 val(Pp)≥val(Dp).
定理2(弱对偶) 问题(P)和(D)之间的弱对偶成立,即val(P)≥val(D).
假设(clg)∘h为真函数,clg为真的K-递增函数. 因为函数h可能取值+∞,所以定义g(+∞)=+∞.
定义3若下述包含关系成立:
则称点对(g,h)满足约束品性(NCQ).
注1易证式(1)的反包含关系成立,所以式(1)可由下式代替:
所以(p,0,r)∈{(p,0,r): (p,r)∈epi(g∘h)*}∩(X*×{0}×R). 故式(2)成立. 证毕.
定理3(稳定强对偶) 点对(g,h)满足约束品性(NCQ)当且仅当对于任意的p∈X*,val(Pp)=val(Dp),并且(Dp)至少存在一个最优解.
证明:充分性. 若val(Pp)=-∞,则结论显然成立. 设val(Pp)∈R,则(p,(g∘h)*(p))=epi(g∘h)*. 因为点对(g,h)满足约束品性(NCQ),所以
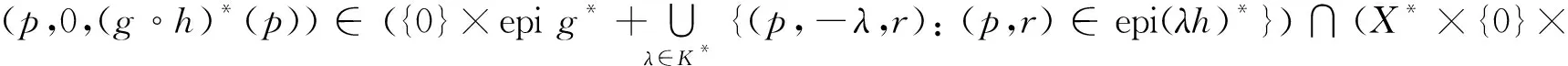

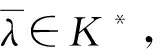
因此点对(g,h)满足约束品性(NCQ). 证毕.
由定理3易得下述强对偶结论:
定理4(强对偶) 若点对(g,h)满足约束品性(NCQ),则val(P)=val(D),并且(D)至少存在一个最优解.
注2当函数f,g为下半连续、h为K-上图闭时,文献[6]的定理5.1借助约束品性(CQ)刻画了问题(P)和(D)之间的强对偶. 而当函数f,g不是下半连续、h不是K-上图闭时,本文借助约束品性(NCQ)刻画了问题(P)和(D)之间的强对偶. 显然本文结果推广并改进了已有的结果.
[1] Burke J V,Ferris M C. A Gauss-Newton Method for Convex Composite Optimization [J]. Mathematical Programming,1995,71(2): 179-194.
[2] Combari C,Laghdir M,Thibault L. A Note on Subdifferentials of Convex Composite Functionals [J]. Archiv der Mathematik,1996,67(3): 239-252.
[3] Zalinescu C. Convex Analysis in General Vector Spaces [M]. Singapore: World Scientific,2002.
[4] ZHENG Xi-yin,Ng K F. Strong KKT Conditions and Weak Sharp Solutions in Convex Composite Optimization [J]. Mathematical Programming,2011,126(2): 259-279.
[5] KOU Xi-peng,PENG Xing-yuan,ZHU Sheng-kun. Second-Order Optimality Conditions for Constrained Set Valued Optimization Problems [J]. Journal of Jilin University: Science Edition,2012,50(2): 244-250. (寇喜鹏,彭兴媛,朱胜坤. 约束集值优化问题的二阶最优性条件 [J]. 吉林大学学报: 理学版,2012,50(2): 244-250.)
[6] Bot R I,Grad S M,Wanka G. A New Constraint Qualification for the Formula of the Subdifferential of Composed Convex Functions in Infinite Dimensional Spaces [J]. Mathematische Nachrichten,2008,281(8): 1088-1107.
[7] Bot R I,Grad S M,Wanka G. Generalized Moreau-Rockafellar Results for Composed Convex Functions [J]. Optimization,2009,58(7): 917-933.
[8] Bot R I. Conjugate Duality in Convex Optimization [M]. Berlin: Springer-Verlag,2010.
[9] LI Chong,FANG Dong-hui,Lopez G,et al. Stable and Total Fenchel Duality for Convex Optimization Problems in Locally Convex Spaces [J]. SIAM Journal on Optimization,2009,20(2): 1032-1051.
[10] Fang D H,Li C,Ng K F. Constraint Qualifications for Optimality Conditions and Total Lagrange Dualities in Convex Infinite Programming [J]. Nonlinear Analysis: Theory,Methods &Applications,2010,73(5): 1143-1159.
[11] Jeyakumar V,Dinh N,Lee G M. A New Closed Cone Constraint Qualification for Convex Optimization [R]. Sydney: University of New South Wales,2004.

