双边群Smash余积的半单性

李德胜， 陈全国,王顶国

(1. 鲁东大学 数学与信息学院， 山东 烟台 264025;2. 伊犁师范学院 数学与统计学院,新疆 伊宁 835000；3. 曲阜师范大学 数学科学学院,山东 曲阜 273165)

0 引言及预备知识

作为Hopf代数的推广,Virelizier[1]建立了Hopf群余代数. 目前,Hopf代数中的许多经典结果已经推广到Hopf群余代数上[2-6]. 作为群Smash余积的推广,本文引入双边群Smash余积的概念,刻画双边群Smash余积的半单性.

假设k是一个域,π是一个群,其单位元为e. 所有代数及余代数均在k上讨论. ⊗k简记为⊗. 给定一个向量空间V,用l(或idV)表示V上的恒等映射. Hopfπ-余代数的概念及性质可参考文献[1-8].

如果H满足下列条件,则H=({Hα}α∈π,{mα}α∈π,{1α}α∈π,Δ,ε)称为Hopfπ-余代数,这里εH:He→k(余单位)和Δ={Δα,β:Hα,β→Hα⊗Hβ}α,β∈π(余乘法)均是k-线性映射：

1) 对任意的α∈π,(Hα,mα,1α)为结合代数;

2) 余乘法满足: ① 对任意的α,β,γ∈π(Δα,β⊗idHγ)∘Δαβ,γ=(idHα⊗Δβ,γ)∘Δα,βγ;② 对任意的α,β∈π,Δα,β均是代数同态;

3) 余单位是代数同态;

4) 存在一簇k-线性映射S={Sα:Hα→Hα-1}α∈π满足：对任意h∈He,

mα∘(Sα-1⊗l)∘Δα-1,α(h)=εH(h)1α=mα∘(l⊗Sα-1)∘Δα,α-1(h).

1)d[0,αβ]⊗d[1,αβ](1,α)⊗d[1,αβ](2,β)=d[0,β][0,α]⊗d[0,β][1,α]⊗d[1,β];

2)εH([d1,e])d[0,e]=d;

3)εD(d[0,α])d[1,α]=εD(d)1α;

4)d[0,α]1⊗d[0,α]2⊗d[1,α]=d1[0,α]⊗d2[0,α]⊗d1[1,α]d2[1,α].

类似地,可以定义左π-H-余模余代数.

1 主要结果

定义1设(C,lρC)和(D,rρD)分别是左π-H-余模余代数和右π-H-余模余代数,定义C,H和D的双边π-Smash余积C×H×D如下：对所有的c∈C,h∈Hαβ,g∈He及d∈D,一簇向量空间C⊗H⊗D={C⊗Hα⊗D}α∈π,其余乘法及余单位分别为

Δα,β(c⊗h⊗d)=c1⊗c2(-1,α)h(1,α)⊗d1[0,β]⊗c2(0,α)⊗h(2,β)d1[1,β]⊗d2,

ε(c⊗g⊗d)=εC(c)εH(g)εD(d).

定理1C×H×D是π-余代数.

证明: 结合π-余代数的定义,容易验证结论成立.

下面假设C和D均为Hopf代数,其对极分别为SC和SD. 通过计算可得:

定理2设C为左π-H-余模余代数和左π-H-余模代数,D为右π-H-余模余代数和右π-H-余模代数. 双边π-Smash余积C×H×D成为Hopfπ-余代数当且仅当对任意的h∈Hα,c∈C,d∈D,

hc(-1,α)⊗c(0,α)=c(-1,α)h⊗c(0,α),hd[1,α]⊗d[0,α]=d[1,α]h⊗d[0,α],

定义2设C和D分别是左π-H-余模余代数和右π-H-余模余代数. 对任意的m∈M,如果一簇向量空间M={Mα}α∈π满足下列条件,则称M为左(C,H,D)-余模:

3)M是左π-H-余模,其余模结构映射为:Mρ={Mρα,β:Mαβ→Hα⊗Mβ}α,β∈π,Mρα,β(m)=m〈-1,α〉⊗m〈0,α〉;

4) 对任意的α,β∈π,m∈Mαβ,

设(C,H,D)M和C×H×DM分别表示左(C,H,D)-余模范畴和左C×H×D-余模范畴. 于是,可建立范畴(C,H,D)M和范畴C×H×DM间的关系如下:

定理3范畴(C,H,D)M和C×H×DM同构.

利用定义2中条件4)和5)易得:

引理1设M为左(C,H,D)-余模,则下列等式成立:

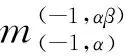
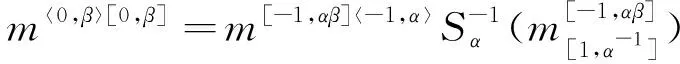
通过计算可得:

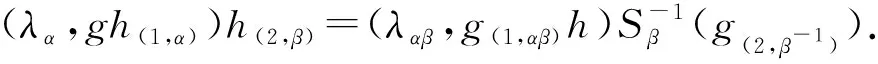
由引理1和引理2可得:

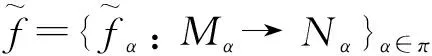
则对任意的n∈Nα,有

推论1设H是一个余半单Hopfπ-余代数,M={Mα}α∈π∈C×HM. 如果N={Nα}α∈π是M的C×H-子余模,且作为左C-余模Ne是Me的直和项,则N视为C×H-余模,也是M的直和项.

[1] Virelizier A. Hopf Group-Coalgebras [J]. Journal of Pure and Applied Algebra,2002,171(1): 75-122.

[2] Zunino M. Double Construction for Crossed Hopf Coalgebra [J]. Journal of Algebra,2004,278(1): 43-75.

[3] Zunino M. Yetter-Drinfel’d Modules for Crossed Structures [J]. Journal of Pure and Applied Algebra,2004,193(1/2/3): 313-343.

[4] WANG Shuan-hong. Group Entwining Structures and Group Coalgebra Galois Extensions [J]. Comm Algebra,2004,32(9): 3437-3457.

[5] WANG Shuan-hong. Group Twisted Smash Products and Doi-Hopf Modules forT-Coalgebras [J]. Comm Algebra,2004,32(9): 3417-3436.

[6] WANG Shuan-hong. Morita Contexts,π-Galois Extensions for Hopfπ-Coalgebras [J]. Comm Algebra,2006,34(2): 521-546.

[7] Montgomery S. Hopf Algebras and Their Actions on Rings [M]. Providence: American Mathematical Society,1993.

[8] CHEN Quan-guo,TANG Jian-gang. A Maschke-Type Theorem for Weakπ-Entwined Modules [J]. Journal of Jilin University: Science Edition,2012,50(4): 603-606. (陈全国,汤建钢. 弱π-缠绕模的Maschke型定理 [J]. 吉林大学学报：理学版,2012,50(4): 603-606.)