一类椭圆方程组Neumann问题正解的唯一性

魏晓丹,周文书,张 友

(1. 大连民族学院 计算机科学与工程学院,辽宁 大连 116600;2. 大连民族学院 理学院,辽宁 大连 116600;3. 大连理工大学 数学学院,辽宁 大连 116024)

考虑如下椭圆方程组Neumann问题正解的唯一性:

(1)

问题(1)与如下稳态捕食-食饵系统有紧密联系：

(2)

(3)

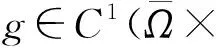
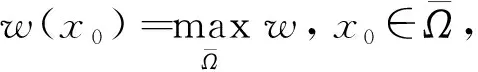
定理1设N≥2. 如果μ>2λ,则问题(1)存在唯一正解.

(4)

因此,只需证明当μ>2λ时,(1,1)是问题(4)的唯一正解.

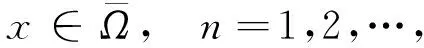
(5)

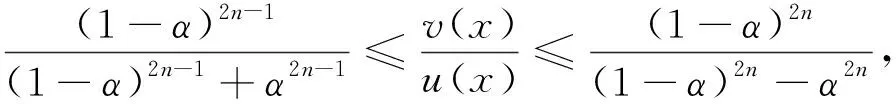
(6)

由于式(6)的证明蕴含在式(5)的证明过程中,因此仅证明式(5). 为此,做变换φ=v/u,则v=φu,对该等式两边微分两次得

Δv=uΔφ+2φu+φΔu,

(7)

从而有

(8)

将式(4)代入式(8)得

(9)

其中α=λ/μ. 由于0<α<1/2,因此

根据引理1中结论2)有

于是

(10)

利用引理1中结论1)得

由此及式(9)可得

又由引理1中结论1)得

于是

(11)

故

假设当n=k(k≥2)时,式(5)成立,即

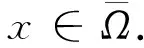
利用左边不等式并注意到式(9)得

由引理1中结论2)得

于是

(12)

由引理1中结论1)得

∀x∈Ω.

由式(9)得

又由引理1中结论1)得

于是

(13)

再由引理1中结论2)得

因此,式(5)得证.

注意到式(5)和(6)分别等价于如下不等式:

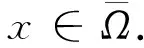
(14)

(15)

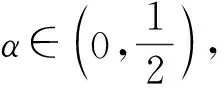
注1设(uβ,vβ)是问题(2)的一个正解,应用定理1及文献[5]中注3.1和注3.2容易证明：如果μ>2λ,则当β→+∞时,有

⇀(1,1)于[H1(Ω)]2,

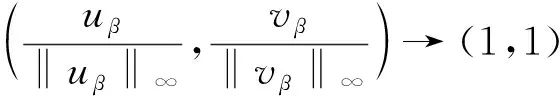
[1] DU Yi-hong,Hsu S B. A Diffusive Predator-Prey Model in Heterogeneous Environment [J]. J Differential Equations,2004,203(2): 331-364.

[2] WANG Ming-xin,Pang P Y H,CHEN Wen-yuan. Sharp Spatial Pattern of the Diffusive Holling-Tanner Prey-Predator Model in Heterogeneous Environment [J]. IMA J Appl Math,2008,73: 815-835.

[3] DU Yi-hong,PENG Rui,WANG Ming-xin. Effect of a Protection Zone in the Diffusive Leslie Predator-Prey Model [J]. J Differential Equations,2009,246(10): 3932-3956.

[4] PENG Rui,WANG Ming-xin. Uniqueness and Stability of Steady States for a Predator-Prey Model in Heterogeneous Environment [J]. Proc Amer Math Soc,2008,136(3): 859-865.

[5] DU Yi-hong,WANG Ming-xin. Asymptotic Behaviour of Positive Steady States to a Predator-Prey Model [J]. Proc Roy Soc Edin,2006,136A: 759-778.

[6] Lopez-Gomez J,Pardo R M. Invertibility of Linear Noncooperative of Linear Noncooperative Elliptic Systems [J]. Nonlinear Analysis,1998,31: 687-699.

[7] ZHOU Wen-shu,WEI Xiao-dan. Uniqueness of Positive Solutions for an Elliptic System [J]. Electronic J Differential Equations,2011,2011: 1-6.

[8] LOU Yuan,NI Wei-ming. Diffusion vs Cross-Diffusion: An Elliptic Approach [J]. J Differential Equations,1999,154: 157-190.