一类非合作椭圆方程组非平凡解的存在性
韦玉程,刘广刚
(1. 河池学院 数学系,广西 宜州 546300;2. 吉林大学 数学学院,长春 130012)
0 引 言
许多实际问题中,偏微分方程(PDE)的解通常与其对应的能量泛函临界点紧密相关,但在证明能量泛函临界点的存在性时,需验证(PS)序列的有界性. 为克服这一困难,Struwe[1]引入了单调性技巧,证明了能量泛函在某种单调性下,可导出(PS)序列的有界性[2]. 之后,该方法被用于极小化问题[3]以及环绕问题[4]中. Jeanjean[5]将单调技巧推广到更抽象的形式中,目前已被应用于其他数学物理方程中[6-10]. 本文基于弱环绕定理[8-9],考虑一类非合作的耦合非线性椭圆方程组,使用单调性技巧证明了该方程组存在非平凡解.
考虑方程
(1)
其中:Ω⊂RN(N≥3)为光滑有界域;F(x,u,v)∈C1(Ω×R2,R). 为方便,记z=(u,v). 假设条件如下:
(H0) (关于x∈Ω一致成立;

(H2) |F(x,z)|=o(|z|),当|z|→0时,关于x∈Ω一致成立;
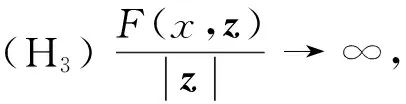
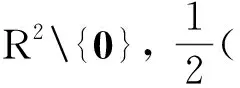
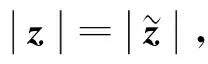
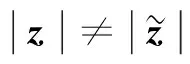
本文的主要结果如下:
定理1假设条件(H0)~(H6)成立,则方程(1)有非平凡解.
例1设F(x,u,v)=(|u|+|v|)p,其中p>2. 显然F(x,u,v)满足假设条件(H0)~(H6).
例2设
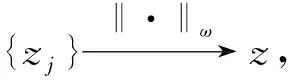
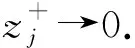
其中:g(x)>0且为周期函数;参数p满足(H1)及0<ε 不难验证F(x,u,v)也满足条件(H0)~(H6). 用‖·‖Lq表示Lq(Ω,R)空间的范数. 记 H={u:Ω→R|u绝对连续,且u|∂Ω=0,|u|∈L2(Ω,R)}. ∀z∈E. 由文献[11]中命题1.1知,存在常数a0>0,使得 ∀z∈E. (2) 定义泛函 (3) 则由经典结果知式(3)的临界点即为方程(1)的弱解. 由假设条件知I∈C1(Ω×R2;R). 记Lz=(-Δu,Δv)T,则线性算子L具有如下特征值: …≤-λm≤…≤-λ2≤-λ1<λ1≤λ2…≤λm…, 且λm→ ∞(m→ ∞). 记E0=KerL,E-与E+分别表示L的负特征子空间与正特征子空间, 则E=E0⊕E+⊕E-. 显然0∉σ(L). 对任意的z∈E,z=z++z-(z±∈E±), 则有 (4) 设(E,‖·‖)是一个Hilbert空间,正交分解为E=N ⊕N⊥,其中N ⊂E为闭的可分子空间. 对于任意的n∈N,存在一个范数‖·‖ω,使得其诱导的拓扑与N上的弱拓扑在有界子集上等价,且‖n‖ω≤‖n‖. 在E中引入范数‖z‖w=‖n‖ω+‖n⊥‖(z=n+n⊥). 对于E=E+⊕E-,z0∈E+且‖z0‖=1,取N =E-⊕Rz0,记 对于E上形如Iλ(z)=J(z)-λK (z)的泛函,可得如下弱环绕定理. 引理1(弱环绕定理) 若对任意的λ∈[1,2],Iλ∈C1,且满足如下假设条件: 1) ∀z∈E,K(z)≥0,I1=I; 2) 当‖z‖→∞时,J(z) → ∞或K(z) → ∞; 则对几乎所有的λ∈[1,2],存在E中的序列{zj},使得 (zj) → 0; Iλ(zj) →cλ, 证明参见文献[8-9]. 为了对方程(1)使用引理1,考虑将泛函(4)写成如下形式: (5) 引理2假设(H0)~(H6)成立,则: 1) 存在不依赖于λ的常数ρ>0,使得κ∶=inf Iλ(Dρ)>0,其中Dρ∶={z∈E+|‖z‖=ρ}; 2) 取定z0∈E+,‖z0‖=1,对任意的λ∈[1,2],存在常数R>ρ>0,使得sup Iλ(∂Q)≤0. 其中Q∶={z=v-+sz0|s≥0,v-∈E-,‖z‖ 证明: 1) 由(H1)及(H2)知,∀ε>0,∃Cε使得 F(x,z)≤ε|z|+Cε, (6) 再由(H4)得 (7) 任取z∈E+,有 ‖z‖p. (8) 注意到 这与式(8)矛盾. 引理3假设(H0)~(H6)成立,则对几乎所有的λ∈[1,2],存在E上的序列{zj},使得 引理4假设(H0)~(H6)成立,则对几乎所有的λ∈[1,2],存在zλ∈E,使得: 3) Iλ(w-zλ)≤Iλ(zλ),∀w∈Σ∶={szλ+v-|s≥1,v-∈E-},w≠0. (9) 从而 这与IΩ(zj)>κ矛盾,故式(9)成立. 由(H4)及Fatou引理,得 即1)和2)成立. 下证3). (10) 重写Iλ(z)为 (11) 由1)知 取w=szλ+v-∈Σ,运用式(10)~(12),直接计算得 引理5假设(H0)~(H6)成立,则存在λj→1(j→∞)及序列{zj}⊂E,使得: 1) sup ‖zj‖<∞; 矛盾. 引理6引理5所得的序列{zλj}是泛函I的一个(PS)序列,且满足: 证明: 对 用引理5可得结果. 同理 于是 K∶={z∈E|I ′(z)=0};c∶=inf{I (z)|z∈K{0}}. 对任意的z∈K,z≠0,由(H4)知 从而c≥0. 设zj∈K{0},使得I (zj)→c. 由引理5知{zj}有界,又由上述断言知(有必要可取子列),zj⇀z∈K{0};再由(H4)及Fatou引理得 即存在z∈K{0},I (z)=c>0. 衷心感谢吉林大学数学学院史少云教授的悉心指导. [1] Struwe M. The Existence of Surfaces of Constant Mean Curvature with Free Boundaries [J]. Acta Math,1988,160(1): 19-64. [2] Ambrosetti A,Struwe M. Existence of Steady Vortex Rings in an Ideal Fluid [J]. Arch Rat Mech Anal,1989,108(2): 97-109. [3] Struwe M. Existence of Periodic Solutions of Hamiltonian Systems on Almost Every Energy Surface [J]. Boletim Soc Bras Mat,1990,20(2): 49-58. [4] Struwe M. Une Estimation Asymptotique Pourle Modèle Ginzburg-Landau [J]. CR Acad Sci Paris: Ser Ⅰ Math,1993,317(7): 677-680. [5] Jeanjean L. On the Existence of Bounded Palais-Smale Sequences and Application to a Landesman-Lazer Type Problem Set on RN[J]. Proc Roy Soc Edinburgh: Sect A Math,1999,129(4): 787-809. [6] CHEN Guan-wei,MA Shi-wang. Periodic Solutions for Hamiltonian Systems without Ambrosetti-Rabinowitz Condition and Spectrum 0 [J]. J Math Anal Appl,2011,379(2): 842-851. [7] CHEN Guan-wei,MA Shi-wang. Homoclinic Orbits of Superlinear Hamiltonian Systems [J]. Proc Amer Math Soc,2011,139(11): 3973-3983. [8] Schechter M,ZOU Wen-ming. Weak Linking Theorems and Schrödinger Equations with Critical Sobolev Exponent [J]. ESAIM: Control Optim Calc Var,2003,9: 601-619. [9] Schechter M,ZOU Wen-ming. Weak Linking [J]. Nonlinear Analysis: Theory,Method and Applications,2003,55(6): 695-706. [10] YANG Min-bo. Ground State Solutions for a Periodic Schrödinger Equation with Superlinear Nonlinearities [J]. Nonlinear Analysis: Theory,Method and Applications,2010,72(5): 2620-2627. [11] Mawhin J,Willem M. Critical Point Theory and Hamiltonian Systems [M]. New York: Springer-Verlag,1989. [12] Willem M. Minimax Theorems [M]. Boston: Birkhäser,1996.1 预备知识

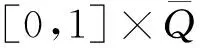

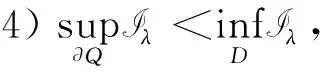







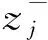
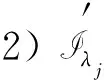

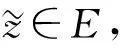
2 定理1的证明





