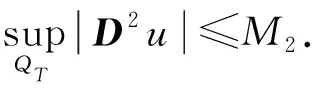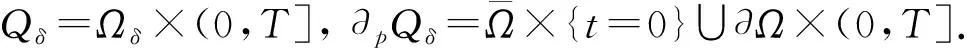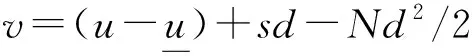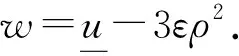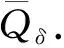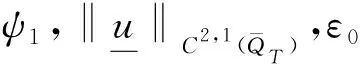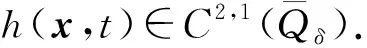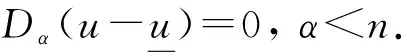一类抛物型k-Hessian方程
任长宇,牛 颖,袁洪君
(吉林大学 数学学院,长春 130012)
0 引言及主要结果

(1)
文献[7]中,取
其中Ω为 Rn中的严格k-1-凸区域. 为了得到解的最大模估计,文献[6-7]对ψ有增长阶的限制:
|ψ(x,t,z)|≤C0(1+|z|), ∀(x,t,z)∈QT×R.
(2)
本文考虑如下抛物型k-Hessian方程第一初边值问题:
(3)

即
∀1 如果λ(D2u)∈Γk,则称一个C2类函数u为可容许函数,也称函数u是k-凸的. 显然,对于可容许函数u,问题(3)中的方程为抛物型完全非线性偏微分方程. 基本假设条件如下: (H3) 问题(3)中ψ和φ满足直到二阶为止的衔接条件. 本文的主要结果如下: 定理1假设条件(H1)~(H3)成立,则问题(3)存在可容许解u∈K,其中 若ψu≥0,则解是唯一的. -Dtφ(x,t)+F(D2φ(x,t))=ψ(x,t,φ(x,t)), ∀(x,t)∈Ω×{t=0}. 令v(x,t)为如下以t为参数椭圆方程Dirichlet问题的解: (4) 对于ut的估计,有如下结论: 显然,如果G在边界∂pQT上某点P0达到其最小值,则存在一个可控常数C>0,使得ut≥-C. 假设G在QT内部某点P0达到其最小值,不妨设该最小值为负数,则有 (5) ujt+(M-u)-1utuj=0, (6) 并且矩阵 (uijt+(M-u)-1(uituj+ujtui+utuij)+2(M-u)-2uiujut)=(uijt+(M-u)-1utuij)≥0. (7) 对问题(3)中的方程关于t微分,有 -utt+Fijuijt=ψt+ψuut, (8) 因此,存在可控常数C>0,使得ut≥-C. 类似地可估计ut的上界. 令G=ut(M+u)-1. 如果G在边界∂pQT上某点P0达到其最大值,则存在一个可控常数C>0,使得ut≤C. 假设G在QT内部某点P0达到其最大值,则有 证明:由定理2,只需估计|Du|在QT内部的界即可. 考虑检验函数 W=weav2, 将式(13)两端同时乘以w2Fij,有 wFijwij-Fijwiwj+2aw2vFijvij+2aw2Fijvivj≤0. (15) (16) 于是 (17) 由式(16)可得 从而 再由式(17),有 (18) 为了估计式(18)的右端项,将问题(3)中的方程关于xk微分,两边同乘uk后再求和,得 (19) (20) 由式(12),(16)有 (21) 将式(20),(21)代入式(15)得 即 注意到Fijuij=k,并且上式右侧有界,因此存在可控常数C1>0,使得2a(1-2av2)Fijuiuj≤C1. 选择a>0充分小,使得(1-2av2)≥1/2,则有 Fijuiuj≤C, (22) 这里C>0为可控常数. 不失一般性,可以假设矩阵(uij)在P0点是对角矩阵. 因此,在P0点 还可以假设在P0点|Du|≤nu1. 由式(12),(16),u11=-2avw2<0. 利用f(λ)的如下性质[9-10]: ∀λ∈Γk,λj<0, 从而可得|Du|≤M1. 定理5的证明可以分为|D2u|在QT抛物边界∂pQT上的先验估计和在QT内部的先验估计两部分. 1) |D2u|在∂pQT上的先验估计. 由问题(3)的初值条件,u(x,0)=φ(x,0),∀x∈Ω,所以只需做u(x,t)在∂Ω×[0,T]上的估计即可. 对∀x0∈∂Ω,通过适当的坐标平移和旋转,不妨设x0为坐标原点,xn为∂Ω的内法向量. 于是在x0附近,∂Ω可表示[8]为 其中κα为∂Ω在x0点的主曲率. 由边值条件u(x,t)=φ(x,t),∀(x,t)∈∂Ω×[0,T]可知,在(x0,t)点,有 ∀α,β≤n-1, (23) 从而得到了u的切向二阶导数估计|uαβ(x0,t)|≤C,∀α,β≤n-1. ∀x∈Ωδ. (24) Lv≤-ε(1+∑Fii), (x,t)∈Qδ,v≥0, (x,t)∈∂pQδ. 证明:由d(x)的定义,对任意的β Ld2=2dLd+2FijDidDjd=2dLd+2Fnn, Ld=-Dtd+FijDijd=FijDijd. 显然存在依赖于∂Ω和δ的可控常数C0>0,使得 |Ld|≤C0(1+∑Fii). (25) 因此 Lv≤C1+C0(s+Nδ)+(C0(s+Nδ)-3ε)∑Fii-NFnn, (x,t)∈Qδ. 不失一般性,可假设f1≥…≥fn,于是有∑Fii=∑fi,Fnn≥fn. 由代数-几何平均不等式,有 ε∑Fii+NFnn≥nε(Nf1…fn)1/n≥εnμ0N1/n=c1N1/n, (26) -Lh≤β(1+∑Fii), (x,t)∈Qδ. 证明:由引理1,可以选择A≫B≫1,使得 Av+Bρ2-h≥0于∂pQδ, L(Av+Bρ2-h)≤0于Qδ. 由抛物算子的极值原理知,Av+Bρ2-h≥0于Qδ. 注意到在(x0,t0)点,Av+Bρ2-h=0,这蕴含了Dn(Av+Bρ2-h)(x0,t0)≥0,即引理2成立. 为了估计可容许解的切、 法方向的混合二阶导数,将问题(3)中的方程关于xm微分,得 -utm+Fijuijm=ψm+ψuum. 显然,对每个m=1,2,…,n,有 (27) |uαn(x0,t)|≤C, ∀α (28) 从而建立了可容许解u在∂Ω×[0,T]上的切、 法方向二阶混合导数的先验估计. 下面做法向的二阶导数Dnnu估计. 由于Δu>0,只需推导出它的上界即可,即 Dnnu≤C于∂Ω×[0,T]. (29) 与估计切向二阶导数时所用的方法(23)一样,在x∈∂Ω点,有 Dξη(u-φ)=-Dν(u-φ)Π(ξ,η), 其中:ξ,η为∂Ω在x点的单位切向量;ν为单位内法向量;Π(ξ,η)为∂Ω的第二基本型. 引理3存在一致的常数c0>0,使得 d(x,t)=d(λ′(Dξηφ-Dν(u-φ)Π(ξ,η)))≥c0, ∀(x,t)∈∂Ω×[0,T]. 证明:考虑d(x,t)在∂Ω×[0,T]上的最小值点(x0,t0),只需证明d(x0,t0)≥c0>0即可. 在x0点选择一个直角坐标系e1,e2,…,en,使得en为∂Ω的内法方向,(Dαβu(x0,t0))(1≤α,β≤n-1)为对角矩阵,并且D11u(x0,t0)≤…≤Dn-1,n-1u(x0,t0). 由d(x,t)的定义知, 根据文献[8]中引理6.2,对(x0,t0)点附近的点(x,t)∈∂Ω×[0,T],有 (30) 于是对于边界∂Ω×[0,T]上(x0,t0)点附近的点,由式(23)有 (31) (32) 其中 下面证明式(29). 由引理3知 ∀(x,t)∈∂Ω×[0,T]. 假设Dnnu(x,t)没有上界,则由文献[8]中引理1.2及Sk(λ)的严格单调性,有 矛盾. 从而式(29)成立. 其中a>0为待定常数. 显然只需得到W的上界估计即可. 在(x0,t0)处微分问题(3)中的方程两次,再利用先验估计及函数F的凹性,有 其中C>0为可控常数. 式(34)两端同时乘以Fiiλ1,对1≤i≤n求和,再利用式(37),(33),(35)及(36)有 (38) 注意到Sk(λ)的一个性质[11]: 则有f1λ1≥Cn,k,其中Cn,k>0为仅依赖于n,k的常数. 于是由式(38)即可得到λ1的上界. 综合1),2),即可完成定理5的证明. [1] Chow B. Deforming Convex Hypersurfaces by the Square Root of the Scalar Curvature [J]. Inventiones Mathematicae,1987,87: 63-82. [2] Andrews B,McCoy J. Convex Hypersurfaces with Pinched Principal Curvatures and Flow of Convex Hypersurfaces by High Powers of Curvature [J]. Trans Amer Math Soc,2012,364(7): 3427-3447. [3] Ivochkina N M,Ladyzhenskaya O A. The First Initial-Boundary Value Problem for Evolutions Generated by Traces of Ordermof the Hessian of the Unknown Surface [J]. (Russian) Acad Sci Docl Math,1995,50(1): 61-65. [4] LIU Hui-zhao,WANG Guang-lie. The First Initial-Boundary Value Problem for the Complete-Nonlinear Parabolic Equations Generated by Eigenvalues of Hessian Matrix [J]. Acta Scientiarum Naturalium Universitatis Jilinensis,1998(1): 27-37. (刘辉昭,王光烈. Hessian矩阵特征值生成的完全非线性抛物方程第一初边值问题 [J]. 吉林大学自然科学学报,1998(1): 27-37.) [5] REN Chang-yu. The First Initial-Boundary Value Problem for Fully Nonlinear Parabolic Equations Generated by Functions of the Eigenvalues of the Hessian [J]. J Math Anal Appl,2008,339(2): 1362-1373. [6] WANG Xu-jia. A Class of Fully Nonlinear Elliptic Equations and Related Functionals [J]. Indiana Univ Math J,1994,43(1): 25-54. [7] CHOU Kai-seng,WANG Xu-jia. A Variational Theory of the Hessian Equation [J]. Comm Pure Appl Math,2001,54(9): 1029-1064. [8] Caffarelli L,Nirenberg L,Spruck J. The Dirichlet Problem for Nonlinear Second-Order Elliptic Equations,Ⅲ: Functions of the Eigenvalues of the Hessians [J]. Acta Math,1985,155(1): 261-301. [9] LI Yan-yan. Some Existence Results for Fully Nonlinear Elliptic Equations of Monge-Ampere Type [J]. Comm Pure Appl Math,1990,43(2): 233-271. [10] Guan B. The Dirichlet Problem for Hessian Equations on Riemannian Manifolds [J]. Calc Var Part Differ Equa,1999,8(1): 45-69. [11] WANG Xu-jia. Thek-Hessian Equation [C]//Geometric Analysis and PDEs. Lecture Notes in Math. Dordrecht: Springer,2009: 177-252.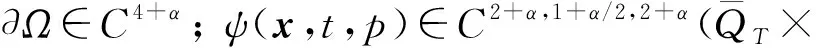

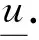

1 解的一阶导数估计
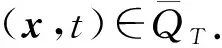


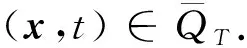
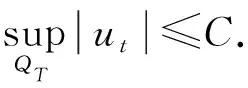
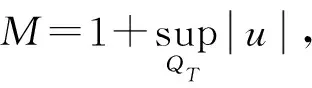

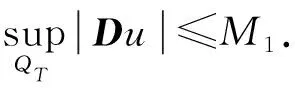
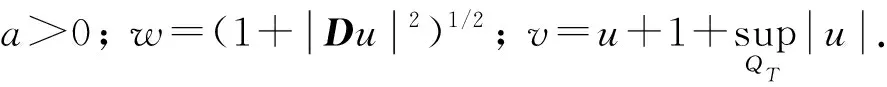
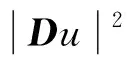
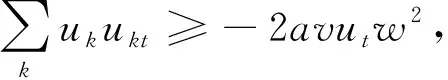

2 解的二阶导数估计