模糊数学在校园安全评价中的应用研究

景国勋，张永强，吕晓燕

(河南理工大学 安全科学与工程学院，河南 焦作 454003)

模糊数学在校园安全评价中的应用研究

景国勋，张永强，吕晓燕

(河南理工大学 安全科学与工程学院，河南 焦作 454003)

在问卷调查的基础上，建立了校园安全等级划分与评价指标系统，确定了安全环境、安全教育、安全管理和事故管理4个一级指标以及校外交通、校外饮食、校外治安等17个二级指标，并运用模糊数学确定了各个量化指标的权重，建立了模糊综合评价量化模型。同时，结合某学校的现实情况进行等级划分及评价计算，对量化指标的可行性及合理性进行了验证，研究结果对加强校园安全管理、提升校园安全水平具有参考价值和指导作用。

校园安全；模糊综合评价模型；安全评价；模糊数学；层次分析法

学校是学生求知的场所。在我国，共有4亿多的在校学生，这是一个相当庞大的社会群体。可是，随着社会经济的发展和校园社会化改革体制的深入，各类矛盾不断产生，安全隐患以及各种各样的安全问题也以各种不同的形式出现在校园中。校园暴力、食物中毒、疾病流行、校舍倒塌、校园火灾、自杀、他杀等安全事故的不断出现，使得校园安全已经成为一个公共话题。但是，就目前来说，针对校园安全方面的研究并不多，对于校园安全等级划分的研究更是少之又少，即使这些为数不多的研究，大部分都停留在定性评价上，定量评价、定量等级划分还处于起步阶段。本文旨在建立通用的校园安全评价的指标体系，对校园安全等级进行量化，并对校园的安全状况进行安全等级划分。

在校园安全评价过程中，涉及到很多影响因素，如在校学生的人数、受教育的级别、学生所处的年龄阶段、校园所处的地理位置、校园周边的社会环境等，其中的相当一部分影响因素带有模糊性。鉴于评价对象的特殊性以及影响因素的多样性，在选择评价理论上要特别注意与之相适应。模糊数学在解决不确定性问题上具有突出的优势[1]，它不仅可以实现校园安全评价主观和客观上的相对统一，而且对校园安全评价中一些难以避免的模糊概念也能够使之量化，这是其他评价方法无法替代的。

一、模糊综合评价的数学模型

(1)确定评价对象的因素论域。U={u1,u2,…,up}也就是p个评价指标。

(2)确定评语等级论域。V={v1,v2,…,vm}，即等级集合，每个等级可对应一个模糊子集。

对m的选取既不能太大也不能太小，因为那样不易判断等级归属。m的取值要便于判断被评事物的等级属性。

(3)进行单因素评价，建立模糊关系矩阵R。在构造了等级模糊子集后，就要逐个对被评事物的每个因素ui进行量化，也就是确定从单元素来看被评事物对各等级模糊子集的隶属度〈R|ui〉，进而得到模糊矩阵R。

矩阵R中第i行第j列元素rij表示某个被评事物从因素ui来看对vj等级模糊子集的隶属度，一个被评事物在某个因素方面的表现是通过模糊向量来刻画的，而在其他评价方法中多是由一个指标实际值来刻画的。因此，从这个角度来说模糊综合评价要求寻找更多的信息。

(4)确定评价因素的模糊权向量集。一般情况下，评价因素对被评事物并非是同等重要的，各方面因素的表现对总体表现的影响也是不同的。因此，在合成之前，要确定模糊权向量。常用的确定权的方法主要有以下几种：

第一，德尔菲法(Delphi)。德尔菲法也称为专家法，在实际运用中较常见，它的特点是集中专家的经验和意见，确定各指标的权数，并在不断地反馈和修改中得到满意的结果，发挥专家集体的智能团作用，对预测对象的未来发展趋势及状况作出正确的判断。“头脑风暴法”就是专家预测法的具体运用。但是，专家会议也有不足之处，有时候心理因素对判断结果影响较大，易屈服于权威或是大多数人的意见，易受劝说性意见的影响，碍于情面不愿意轻易改变自己已经发表过的言论等。

第二，模糊层次分析法(Fuzzy AHP)。模糊层次分析法是将与决策相关的条件分解成目标、准则、方案等若干层次，以此为基础进行定性、定量分析的决策方法。它是在对复杂的决策问题的本质、影响原因及其内在关联等进行深入分析的基础上，利用较少的定量化信息使决策的思维过程呈现数学化，从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法，尤其适合于对决策结果难以直接准确采用数学方法进行计量的场合。本文采用的是模糊层次分析法来确定各个影响因素的权重[2]。

第三，确定模糊评判矩阵A。按照测评对象的要求，由参加评价的人员对所参评的因素两两进行比较打分，然后汇总数值，利用对称三角形模糊数学[3]的加法进行运算来确定模糊评判矩阵：A=(aij)n×m,其中aij=R，n的含义为参加测评的总人数[4]。

第四，各个评价指标相对评价对象的权重向量的计算。各个评价指标相对评价对象的权重计算取决于Bij，构成比较矩阵B=(Bij)，式中i、j的取值范围=1,2,3,……n。

第六，对各级评价因素进行模糊综合评价。模糊综合评价是那些受大量的模糊因素影响的评价对象应用广泛的综合评估方法[5]。在复杂的系统中，需要考虑的因素往往很多，因素还要分成若干层次，形成评判树状结构，对各层次的因素划分评判等级，各层次划分的评判等级数目应相同，上一层次与下一层次划分的评判等级要有统一的对照关系，便于进行数学基础运算，并确定各因素的隶属函数，求得各层次的模糊矩阵。评判顺序为:首先进行最低层次的模糊综合评判，其次由最低层次的评判结果构成上一层次的模糊评判矩阵，再进行上一层次的模糊综合评价，循此自下而上逐层进行模糊综合评价，就可以得到系统总体的综合评判结果。如果存在二级标准或三级标准，按相同的方法依照次序逐层合成，直至得到最后评价结果为止。

二、校园安全评价的实例分析

通过对某校调研及问卷调查分析，采用校园安全等级划分方法确定其所处等级，运用层次模糊综合评价模型，由评估专家以及随机选取的参评学生对该校的安全指标进行打分，然后对这些分值进行分析和计算来测定该校所处的安全等级。具体过程如下：

(1)确定因素集。U={u1,u2,u3,u4}={安全环境，安全教育，安全管理，事故处理}，其中，u1={u11，u12，u13，u14，u15，u16}={校外交通，校外饮食，校外治安；校内交通，校内饮食，校内防火防盗及硬件设备}；u2={u21,u22,u23,u24,u25,u26,u27}={心理健康教育，安全意识教育，网络安全教育，安全法规教育，就业安全教育，交通安全教育，安全知识技能教育}；u3={u31,u32,u33}={组织领导机构，安保卫人员配置，安全制度措施}；u4={u41,u42={自我检查，及时整改}；

(2)确定评判集。V={v1,v2,v3,v4,v5}={安全，较安全，一般安全，较危险，危险}，为了便于计算我们分别对等级评语赋值为{90,80,70,60}。那么所对应的评价定量标准如表1所示：

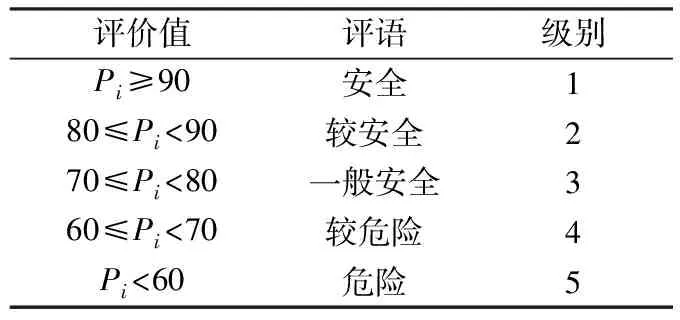
表1 评价定量标准

(3)通过对20位专家问卷及随机抽查100名学生进行问卷调查，构造单因素评判矩阵R1,R2,R3,R4。

(4)根据被评价的实际情况及查阅相关资料，组织专家对两级指标的安全等级进行打分，从而确定两级指标的权重。一级评价指标的权重：

A′=(0.024 1,0.429 5,0.394 5,0.151 8)

一级指标相对于整个评价的比较矩阵为：

二级指标与一级指标之间的比较矩阵为：

A1=(0.277 6,0.013 8,0.036 5,0.013 0,0.107 7,0.551 4)

A2=(0.023 0,0.264 1,0.028 7,0.251 1,0.097 8,0.253 7,0.084 1)

A3=(0.285 5,0.670 7,0.043 8)

A4=(0.900 0,0.100 0)

(5)进行I级模糊综合评价：

B1=A1R1=(0.510 1,0.203 5,0.102 6,0.183 8)

B2=A2R2=(0.400 3,0.338 7,0.179 5,0.048 2)

B3=A3R3=(0.266 9,0.128 6,0.461 6,0.142 9)

B4=A4R4=(0.080 0,0.730 0,0.100 0,0.090 0)

(6)构造I级评判矩阵：

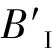
(7)进行2级综合评判：

BⅡ=A′BT=(0.024 1，0.429 5,0.394 5,0.151 8)

此学校的安全等级为一般安全，该校应该进一步加强校园安全工作，尤其是在校园安全环境方面要侧重于校内饮食安全以及校内交通管理的提高。

三、结 论

安全本身具有模糊性，适合用模糊集理论进行评价，评价结果一般为与安全等级相对应的隶属度向量。本文所采用的安全等级特征量及其计算方法，是在分析总结了对校园安全影响因素的基础上，利用安全等级特征模糊特征量及其中值和方差的计算方法来确定校园的安全等级的，采用该方法对校园安全进行定量划分及定量评价，通过实例证明是合理的。

[1] 王琦．实用模糊数学[M]．北京：科学技术文献出版社，1984．

[2] 诸克军,张新兰,肖荔瑾．FuzzyAHP方法及应用[J]．系统工程理论与实践，1997,16(12):61-63．

[3] 刘普寅,吴孟达．模糊理论及其应用[M]．长沙：国防科技大学出版社，1998．

[4] 郑展飞,周直．模糊数学在工程项目风险辨识中的应用研究[J]．重庆交通学院学报，2006,4(2):122-124．

[5] 胡永宏，贺思辉.综合评价方法[M].北京：科学出版社，2000.

[6] 何学秋.安全科学与工程[M].徐州：中国矿业大学出版社,2008.

[7] 景国勋，施式亮.系统安全评价与预测[M].徐州：中国矿业大学出版社，2009.

[8] 皮祖训，刘何清﹒高校事故非线性灰色预测模型及应用研究[J]﹒中国安全科学学报，2009,19(5)：24-31.

[9] 许开立，陈宝智，陈全﹒安全等级特征量及其计算方法[J]﹒中国安全科学学报，1999,9(6)：6-12.

[10] 许开立，陈宝智﹒人—机—环境系统安全性评价的模糊数学方法[J]﹒人类工效学，1999,5(2)：16-19.

[11] 陈守煜﹒系统模糊决策理论与应用[M]﹒大连：大连理工大学出版社，1994:1-98.

[12] 李兴洪，汪群，段钦治﹒工程模糊数学方法及应用[M]﹒天津：天津科学技术出版社，1993:52-57.

[13] 张跃﹒模糊随机变量[J].哈尔滨工程学院学报，1989,22(3)：12-20.

[14] 王光远，张跃﹒模糊随机过程论[M]﹒贵阳：贵州科技出版社，1994:156-230.

[15] 徐大图．建设项目投资控制[M]．北京：地震出版社，1993．

[责任编辑 位雪燕]

河南理工大学学报(社会科学版)，第14卷，第1期，2013年1月

ApplyingTheoriesofFuzzyMathematicstotheEvaluationofCampusSecurity

JINGGuo-xun，ZHANGYong-qiang，LVXiao-yan

(SchoolofSafetyScienceamp;Engineering，HenanPolytechnicUniversity，Jiaozuo454003，Henan,China)

In recent years, with the socialization process of campus and increasing college enrollment, the issue of campus security has become particularly prominent. Based on the results of questionnaire, a common campus security classification and evaluation system is established, and 4 first-level indexes (secure environment, safety education, security management and accident management) and 17 second-level indexes (transportation, food, public security and the rest) are defined. the authors also build a fuzzy comprehensive evaluation model by employing theories of fuzzy mathematics. Combined with the actual situation of an anonymous university, the feasibility and validity of the quantitative indexes are proved. It is hoped that this paper can provide some reference for enhancing safety management and improving campus security.

school safety; fuzzy comprehensive evaluation; safety evaluation; fuzzy mathematics; quantization index

2012-07-08

景国勋(1963—)，男，河南许昌人，教授，博士生导师，主要从事安全系统工程、矿山安全技术的研究工作。

E-mail：zhangyq@hpu.edu.cn

F406.8

A

1673-9779(2013)01-0029-04