基于降低航行阻力的声呐导流罩外形优化

杜礼明，张 进

(大连交通大学 辽宁省高等学校载运工具先进技术重点实验室，辽宁 大连116028)

0 引 言

现代大、中型水面舰艇艇舷底部大多配置了综合声呐设备，但无论是舰艇或潜艇处于航行还是停泊状态，均有较大的水流从声呐传感器表面流过，严重影响声呐的使用效果。因此，需要使用具有良好声透性的材质与具有良好声学特性线型的导流罩加以保护，以提高声呐的信噪比和探测能力［1］。导流罩能起到阻止水流直接冲击传感器的作用，显著降低声呐探测器周围的水流噪声对目标的噪声信号影响，从而可以提高声呐的综合性能。由于导流罩突出于主船体的底部或首部之外，其外形是一个相对复杂的流线型，当舰船航行时，由于其压力分布的不均匀，导致导流罩表面会形成压力脉动，在一定程度上增大了航行阻力［2］。因此，分析导流罩对船体航行产生的影响和优化导流罩线型使其流动阻力最小是非常必要的。

由于舰船航行时，其外部流场十分复杂，形成多种行进阻力。利用传统的试验方法分析导流罩对船体航行的影响，流场性能分析难度高、耗费大，周期长且准确度差。而应用经验公式进行流场压力及阻力估算，得到的计算数值与实际往往有很大偏差，无法给工程实践提供可靠依据。计算流体动力学 (computational fluid dynamics，CFD)在工程中的成熟应用，使得研究者可以利用计算机仿真技术，结合数学模型，代替真实系统进行研究，能够快速探明问题，明显缩短研发周期，减少反复试验造成的浪费，从而显著降低生产成本。本文出于降低导流罩在航行过程中的阻力这一工程现实考虑，采用CFD 方法对某型船加装导流罩前后的航行阻力等流体动力学性能进行数值研究，在此基础上提出4 种导流罩外形结构模型，通过比较分析得到综合性能最佳者，为导流罩外形的结构优化设计提供参考。

1 数学模型与计算网格

1.1 理论基础

1)守恒定律

船舶在水中航行遵循基本的流体定律，这些守恒定律包括:质量守恒定律、动量守恒定律和能量守恒定律。本文模拟分析的是加装导流罩前后某型船在水中的航行情况。该船在满载出港排水量下，海况小于2 级，风力小于蒲氏3 级，主机转速为1 000 r/min 时，最大试航航速为16 kn，经济航速为13 kn，本文的流体可以认为处于湍流状态，系统还要遵守附加的湍流输运方程［3］。

质量守恒方程:

式中:ρ 为流体密度;t 为时间;u 为速度矢量。

动量方程:

式中:τ 为微元表而粘性应力;p 为流体微元体上的压力。

能量守恒方程:

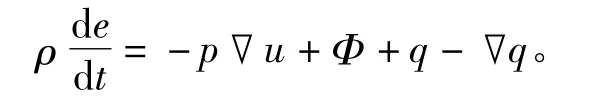
式中:e 为内能;q 为交换热量。

2)标准k－ε 模型

标准k－ε 模型是目前使用最广的湍流模型，具有适用范围广、计算精度合理的优点，是一种针对高雷诺数的湍流计算模型。当遇到弯曲壁面流动、强旋流和逆压梯度较大的问题时，计算精度会降低［4］。当流动不可压且不考虑源项时，定义k 与ε的输运方程为:

式中:Gk为湍动能k 的产生项，各常数C1ε=1.44，C2ε=1.92，σk=1.0，σε=1.3。

1.2 仿真条件

本文采用多相流模型对船舶的航行进行模拟仿真。在计算中水介质取粘性、不可压缩流体，紊流方程采用有适用范围广、经济和合理的精度，且工程流场计算中常用的标准k－ε 湍流模型为主要计算工具，采用耦合式求解器隐式方案对三维Navier－Stocks 方程求解，即同时求解连续方程、动量方程和能量方程，对于给定变量，单元内的未知量用邻近单元的已知和未知值来计算［5－6］。船体选用标准壁面边界，采用动网格技术中的动态层更新法，模拟船的航行过程。上下及壁面边界采用无滑移边界条件，给定法向速度Vn=0

1.3 船吃水线以下部分的仿真模型

由于本文研究导流罩对船速影响，凡与海水相对流动无关的船体结构均不在研究内容之中，因此将船(未加装导流罩)吃水线以下部分简化为图1所示。加装导流罩时导流罩安装在69 ～75#肋骨之间船底下，与船纵向中心面重合，大头朝舰首方向，导流罩轮廓尺寸为2.52 m×1.22 m×1 m，重量为2 500 kg。加装导流罩后的模型与上述模型相似。

1.4 计算网格(空间离散)

针对舰船航行的实际情况，将模型分为4 个区域，其中区域1 为动区域(包括船体在内)，其区域范围随着航行的进行不断变化，为适应其复杂外形特性，运用混合网格进行划分，生成非结构化网格;其他3 个区域形状规则，划分为六面体网格。具体划分情况如图2所示。

图1 原始船仿真模型Fig.1 The original outline of the ship

图2 计算域的完整网格Fig.2 Discrete mesh of the whole computational domain

2 结果与讨论

2.1 声呐导流罩对船行进阻力影响的仿真分析

2.1.1 未加装导流罩的模拟分析

首先模拟分析该船在水中以16 kn 航速航行时加装和不加装声呐导流罩2 种情况的速度分布、压力分布情况，分析导流罩对船行进阻力的影响。

图3 和图4 为船体周围和船体竖直剖面的压力分布。由图可知，船头由于行进过程中对水有压缩作用，使该部位的压力明显升高，而船尾部由于船的行使出现负压区。船头与船尾的压差越大则船的航行阻力越大，为减少船体航行阻力，船头往往设计为流线型就是基于这一原理。

图3 船以16 kn 速度航行时船体所受的压力Fig.3 Pressure distribution of the ship when moving at 16 kn

图4 船以16 kn 速度航行时竖直剖面压力分布Fig.4 Pressure distribution of the vertical profile when the ship moving at 16 kn

图5 和图6 为船以16 kn 速度航行时船体周围速度分布和船的航行阻力。由图可知，由于船体周围流体受到来自不同方向和不同大小的压力，流体速度各不相同，尤其是在船头与船尾部形成一系列漩涡。并且随着迭代次数的增加，航行阻力慢慢趋向稳定，最终阻力值在8.45 × 105Pa左右。

图5 船以16 kn 速度航行时竖直剖面速度分布Fig.5 Velocity of the vertical profile when ship moving at 16 kn

图6 船以16 kn 速度航行时阻力发展情况Fig.6 Resistance of the ship when moving at 16 kn

2.1.2 加装导流罩的模拟分析

图7 和图8 为加装导流罩后船体周围、船底和船体竖直剖面的压力分布。对比图3 和图4，船体底部的压力分布有显著不同。导流罩头部在航行过程中对水有压缩作用，使该部位的压力明显升高，而其尾部由于船的行使出现负压区。这与船头与船尾对水流的作用完全相同。正是由于导流罩头尾的压差形成航行阻力，这个压差越大，船的航行阻力也越大。

图7 船以16 kn 速度航行时船体所受的压力Fig.7 Pressure distribution of the ship when moving at 16 kn

图8 船以16 kn 速度航行时导流罩附近压力Fig.8 Pressure distribution around sonar dome profile when the ship moving at 16 kn

图9 和图10 为加装导流罩后竖直剖面上的压力和速度分布图。对比图4 和图5 可以看出，导流罩的存在会增加船体底部相应位置的压力，并且会在导流罩周围形成多个不同的速度区，增加漩涡数量。

图9 船以16 kn 速度航行时竖直剖面压力分布Fig.9 Pressure distribution of the vertical profile when ship moving at 16 kn

图10 船以16 kn 速度航行时竖直剖面速度分布Fig.10 Velocity of the vertical profile when ship moving at 16 kn

图11 为船以16 kn 速度航行时船的航行阻力发展情况。对比图6 可以看出，由于导流罩增加了船底的漩涡数量，并且使船体在迎流方向上的横截面积也有所增大，因此最后趋向稳定的航行阻力值要明显高于未加装导流罩时的阻力值。

图11 船以16 kn 速度航行的阻力发展情况Fig.1 Resistance developing history when the ship moving at 16 kn

分析以上2 种工况的仿真结果，增加导流罩后，船以16 kn 速度航行时，船底导流罩附近最大压力增加2.4 ×104Pa 左右，船整体航行阻力增加3.4 ×104N 左右。由于导流罩的体积占船体总排水体积的比例很小，大约2% ～4%左右，因此该船加装导流罩前后的船航行总阻力变化不大，二者之间的差值不到5%，具体数值难以估算，也就是相同牵引动力情况下加装导流罩前若最大航速为16 kn，则加装导流罩后最大航速不低于15.2 kn。由于该船的经济航速为12 ～14 kn，故还要对加装导流罩前后航速为12 kn 和13 kn 时的阻力变化进行模拟分析。类似以上的模拟步骤，经过对仿真结果进行分析可知，船速12 kn与13 kn 的流体性能参数基本相同，只是随船速的增大，阻力分布也有所增大，而速度、压力、阻力分布特征完全相同。

2.2 导流罩的外形结构优化

声呐导流罩可视为船身的附体，为了尽可能降低附体阻力，导流罩的外形应符合以下2 点基本要求:

1)具有良好的流线型，避免界层分离;

2)与主船体连接光顺，尽可能沿船体的流线方向安装。

从声呐接收器的要求来看，导流罩周围水的流动应避免分离现象，以免产生旋涡噪声而影响声呐的使用效果。因此，声呐性能和船舶阻力对导流罩外形的要求是一致的。

本文中导流罩是轴对称回转体，由于声呐设备尺寸所限，本文在给定的导流罩基本外形基础上，提出4 种模型并进行模拟和性能比较分析。

1)模型1，头部采用流线型，尾部采用半圆形;

2)模型2，采用与模型1 相反的模型，即头部采用半圆形，尾部采用流线型尖尾;

3)模型3，头部和尾部均采用半圆形;

4)模型4，头部和尾部均采用流线型过渡。

图12 是4 种导流罩的外形构造。为进一步设计出流体力学性能更为优异的导流罩外形，基于流体力学中关于降低阻力的物体外形基本原则，对以上4 种模型进行了深化模拟分析。

图12 4 种声呐导流罩模型Fig.12 Four models of sonar dome profile

2.3 加装4 种导流罩后船在水中航行性能比较

如前所述，由于导流罩的体积占船体总排水体积的比例很小，大约在2% ～4%左右，因此船是否加装导流罩对船的航行速度影响很小，加装导流罩前后二者之间的差值不超过5%，不同导流罩对船速的影响差别就更小，故本文只对加装4 种导流罩后船的总航行阻力进行比较(见表1)。

表1 加装4 种导流罩后船在水中航行的总阻力Tab.1 Resistance of when the ship stalled with sonar dome profile

由于船航行的阻力主要来自航向方向，故表1中特征长度定义为导流罩沿船行方向长度。由表可知，加装4 种导流罩后船在水中的航行阻力基本相同，这是由于导流罩本身航行阻力小的缘故。从表可以看出加装模型4所示的导流罩后船的总阻力最小，加装模型1所示导流罩后船的总阻力次之。模型4所示导流罩会使得导流罩的尺寸明显增大，甚至影响其装载能力，从而会影响整体性能。

综合考虑，模型1 为最佳方案，该模型可以减少船行阻力，有利于减少能量的损耗，提高其利用率，同时又不会引发由于导流罩尺寸明显增大而影响整体性能，为较优形状。

3 结 语

通过对船舶有无导流罩时船体周围的压力、阻力变化情况以及改变导流罩外形后的阻力变化情况的模拟分析，可以得到如下结论:

1)加装声呐导流罩后船的航行阻力有所增大，船体周围的压力分布特征明显不同;

2)随着船航行速度的增大，导流罩附近最大压力和船体的航行阻力也随之增大;

3)由于导流罩的体积占船体总排水体积的比例很小，大约在2% ～4 %左右，因此该船加装导流罩前后的船航行总阻力变化不大，二者之间的差值不超过5%，也就是相同牵引动力情况下加装导流罩前若最大航速为16 kn，则加装导流罩后最大航速不低于15.2 kn;

4)通过详细的数值模拟，对4 种导流罩的结构外形的外流场性能进行了定量分析，并结合其尺寸影响和导流罩内部容纳空间的限制，可以得出在4 种模型中模型1 的综合性能最佳。该模型可以减少航行阻力，有利于减少能量的损耗，提高其利用率，同时又不会引发由于导流罩尺寸明显增大而影响整体性能。为进一步降低导流罩对船速的影响，建议导流罩头部采用流线型而尾部为半圆形结构。

［1］王影东．声呐导流罩的线性优化［D］．哈尔滨:哈尔滨工程大学，2008．

［2］盛振邦，盛正为，杨阿康，等．声纳导流罩的外形设计［J］．船舶工程，1979(3):42－46．

［3］孙丽，刘贵杰，王猛，何波．AUV 导流罩外流场数值仿真与几何参数优化［J］．计算机仿真，2011(5):188－192．

［4］张晓东，张培林，等．k－ε 双方程湍流模型对制退机内流场计算的适用性分析［J］．爆炸与冲击，2011(5):516－520．

［5］韩占忠，工敬，兰小平．FLUENT 流体工程仿真计算实例与应用［M］．北京:北京理工大学出版社，2004．

［6］周俊波，刘洋．FLUENT6．3 流场分析从入门到精通［M］．北京:机械工业出版社，2012．