螺旋桨水动力性能计算粘性流体CFD方法的应用与研究
叶剑平,庄光宇
(1.海军驻719 所军事代表室,湖北 武汉430064;2.中国人民解放军92857 部队,北京102444)
1 概 述
计算流体力学[1](computational fluid dynamics,CFD)通过计算机数值计算和图像显示,对包含有流体流动和热传导等相关物理现象的系统进行分析。其基本思想可以归结为:把原来在时间域及空间域上连续的物理量的场,如速度场和压力场。用一系列有限个离散点上的变量值的集合来代替,通过一定的原则和方式建立起关于这些离散点上场变量之间关系的代数方程组,然后求解代数方程组获得场变量的近似值。CFD 方法对流体流动进行数值模拟的过程,通常包括以下几方面:
1)建立问题中反映各个量之间关系的基本微分控制方程(通常包括质量守恒方程、动量守恒方程、能量守恒方程等)及相应的定解条件。
2)寻求离散化控制方程的数值方法(如有限差分法、有限元法、有限体积法等),贴着螺旋桨表面建立坐标系,边界条件的处理等。
3)划分网格、输入初始条件和边界条件、设定控制参数等。
4)通过图表等方式显示计算结果,对质量和结果进行检验检查和判断分析,得出结论。
粘性流体CFD 计算的控制方程是N-S 方程,其主要的湍流数值模拟可分为直接模拟数值方法(DNS)、大涡模拟方法 (LES)和雷诺平均方法(RANS)。DNS 方法直接用瞬态的N-S 方程对湍流进行计算,无需对湍流流动作任何简化和近似,理论上可以得到比较准确的计算结果;LES 方法采用空间过滤后的瞬态N-S 方程来模拟湍流中的大尺度涡,而被过滤掉的、比网格尺度小的涡,是通过近似的模型来考虑其对大涡的影响;RANS 方法的核心是不直接求解瞬时的N-S 方程,而是求解时均化的N-S 方程,这样的近似,既可以避免DNS 方法计算量大的问题,其精度也可满足工程实际应用的要求。由于螺旋桨周围流场的复杂性以及目前计算机的性能所限,DNS 方法和LES 方法还很少应用于螺旋桨周围湍流场的模拟计算,更多的是通过RANS方法来进行数值模拟。目前,在研究螺旋桨方面,RANS 方法是使用最广泛、技术最成熟的湍流数值模拟方法。
1988年,Stern 等[2]应用升力面方法得到螺旋桨载荷分布,代入粘性流体CFD 方法的流场控制方程作为源项,进行了船桨干扰下船舶流场的计算工作。1997年,唐登海等[3]在求解船舶螺旋桨周围粘性流场的数值解时,应用直接求解RANS 方程的方法。分析了由于粘性流动引起的螺旋桨周围及螺旋桨尾流场的一些重要特征。1998年,第22 届ITTC会议曾组织了一个专题[4]对面元法和RANS 方法进行实例计算比较。通过比较发现,RANS 方法和面元法都可较准确地预报螺旋桨的敞水性能以及桨叶表面的压力分布,说明RANS 方法已经比较成熟,可成为螺旋桨设计和性能预报的有力工具。2003年,Rhee 等[5]采用混合空泡模型模拟计算了螺旋桨定常空泡流动,计算得到的螺旋桨敞水性能结果同试验测量结果非常接近,模拟出的空泡初生以及空泡形状同试验观测结果比较相似。2007年,Mikkelsen 等[6]用RANS 方程研究船后螺旋桨性能时,在桨前方用1 个鼓动盘来产生所需的非均匀船体伴流,计算结果显示这种方法可以用来研究工作于船后尾流场中的螺旋桨。2009年,Vladimir Krasilnikovl 等[7]采用RANS 的方法研究了几何参数对螺旋桨诱导流场的影响。计算了不同盘面比、侧斜和叶数情况下螺旋桨的诱导流场,在此基础上,进一步分析了这些参数对螺旋桨尾流场的影响。从计算结果可看出,桨叶盘面比和侧斜的增大都会使螺旋桨的诱导流场变小;叶数的变化主要影响着盘面内螺旋桨诱导流场的周期数。2010年,王超等[8]结合RNG k-ε 湍流模型,运用滑移网格技术对粘性流场中桨舵相互干扰引起的三维非定常湍流进行了计算,并与试验测量值作了比较。从对计算结果的分析可知,利用滑移网格技术及RNG k-ε 湍流模型,可以较好地模拟桨舵干扰的水动力性能问题。目前,RANS 方法在组合推进器、空泡性能预报乃至螺旋桨设计等问题上的应用也已相当广泛。
2 计算模型的建立
以DTRC4119 桨为研究对象,建立模型及进行网格划分、边界条件设定,给出湍流模型的选择和求解控制参数的设置,梳理螺旋桨的水动力性能预报、螺旋桨的尾流场模拟与分析的整个过程。DTRC4119 桨的主参数[9]见表1。
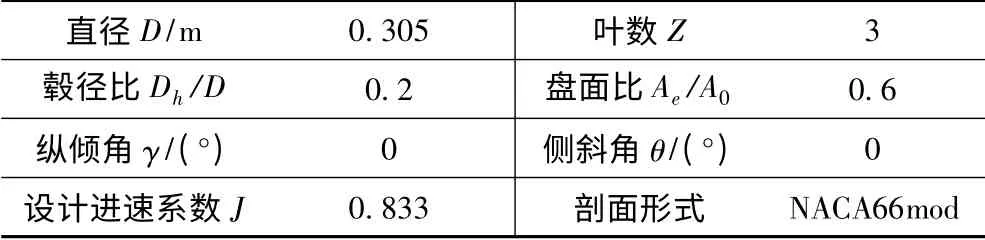
表1 DTRC4119 桨的主参数Tab.1 The primary parameter of DTRC4119 propeller
2.1 计算网格划分与数值模拟参数设定
采用CFD 数值模拟螺旋桨的敞水试验。鉴于来流均匀和螺旋桨几何上的周期性,为减少计算时间,提高计算效率,可只取单个桨叶所在的单通道(周向展开120°)作为计算域。计算模型见图1。在建模过程中使用的是直角坐标系O-XYZ。计算域的内边界取在桨毂和叶片表面上,其中桨毂模拟敞水试验;外边界面取在直径约为螺旋桨直径5 倍的圆柱体表面上。为计算的需要,又把整个域分成1 个小域和1 个大域,这样便于在划分网格时进行局部加密,提高计算结果的准确度。网格划分是CFD 模拟过程中的重要环节。靠近桨叶和桨毂表面的这层非结构网格尺度为直径的1/200 左右,以保证网格y+值的取值范围(30 <y+<300)。同时,在划分网格时使用了局部加密的方法,对于桨叶与桨毂的连接处以及叶梢部分等进行局部加密,以便捕捉到重要的流场信息。螺旋桨表面及周围流场网格划分如图2所示。

图1 单通道数值模拟模型Fig.1 Single chanel numerical simulate model

图2 网格划分示意图Fig.2 Sketch map of reseau partition
计算区域包括的边界条件有:入口边界、出口边界、桨叶和桨毂表面、扇形柱状侧面。本文选用Fluent 软件提供的运动参考坐标系模型(即MRF 模型),进口边界和扇形柱体圆弧面设定为速度进口条件,出口边界设定为压力出口,桨叶和桨毂表面为无滑移物面边界条件,扇形柱状大域、小域两侧面设定为旋转周期性边界条件,转动区域(小域)与静止区域(大域)的交界面设为交换面。计算域内的流体则按MRF 模型设置为绕x 轴以角速度N/rpm 旋转。
2.2 湍流模型的选择与求解控制参数的设置
计算时,湍流模型的选择与求解控制参数的设置见表2。一般迭代1 000 步左右即可收敛。

表2 各类数值格式和选项的设置Tab.2 The numeric format and the option settings
3 计算结果与分析
3.1 敞水性能计算
对于舰船螺旋桨需要计算:桨推力T,桨扭矩Q,螺旋桨转速n,水流进速VA。为了便于比较分析,通常均以桨直径无因次化。
进速系数
桨推力系数
桨扭矩系数
推进效率

3.2 敞水性能计算结果及与试验结果对比
进速系数J 分别取为0.5,0.7,0.833,0.9 和1.0,螺旋桨转速为一定值n=900 r/min。表3 分别列出了在不同进速系数下,得到的螺旋桨推力、扭矩和推进效率计算值与试验值的比较结果。图3 绘出敞水特征曲线结果比较。

表3 DTRC4119 敞水性能比较Tab.3 The hydrodynamic open water performance of DTRC4119 propeller

图3 螺旋桨敞水性能比较Fig.3 The hydrodynamic open water performance of propeller
对比表3 和图3 中螺旋桨水动力性能计算值与试验值可知,计算所得的Kt 曲线与10Kq 曲线都比试验值略高,这应该是由于空泡的存在所导致。在试验中,吸力面上低于饱和压力的区域出现了空泡,空泡区的压力保持为饱和蒸汽压力;而数值模拟时,由于未使用特定的空化模型,所以导致模拟得到的Kt 与10Kq 值存在一定的误差。总的来说,在设计工况J=0.833 处吻合得最理想,在考察的进速系数范围内(0.5 ~1.1),推力系数Kt、扭矩系数Kq 以及敞水效率η 的计算结果与试验结果吻合较好,推力系数Kt 误差在2.4%以内,扭矩系数Kq 误差在1%以内。在高进速系数下,由于考察值的绝对量已经很小,所以计算值微小的变化都会造成误差相应增大。说明在有关螺旋桨敞水性能的计算中,采用CFD 软件进行的数值模拟结果可以满足工程应用的要求。
3.3 螺旋桨的剖面压力分布比较
以DTRC4119 桨为例,将压力分布的CFD 计算结果与试验测量结果[10]以及Hoshino[11]采用面元法的计算结果进行比较,进速系数J 取0.833,比较结果见图4 ~图6。在0.3R 剖面处,CFD 计算结果和实验结果相比较整体偏高,但是二者的形状基本相似,整体趋势基本相当,与面元法计算结果的精度大致相同;在0.7R 和0.9R 剖面处,除了在导边和随边的附近CFD 计算结果和实验结果稍有差别外,其他地方的压力分布吻合很好,虽然导边附近和随边附近的压力分布计算结果和试验结果有差别,但整个叶切面压力分布的整体趋势基本相当。说明CFD 的计算方法能较好地计算螺旋桨定常状态下的压力分布。

图4 P4119 r/R=0.3 处剖面压力分布比较Fig.4 P4119 r/R=0.3 section pressure distributions

图5 P4119 r/R=0.7 处剖面压力分布比较Fig.5 P4119 r/R=0.7 section pressure distributions

图6 P4119 r/R=0.9 处剖面压力分布比较Fig.6 P4119 r/R=0.9 section pressure distributions
3.4 螺旋桨尾流场的数值模拟
图7 ~图9 为CFD 计算的螺旋桨DTRC4119 在x/R=0.295,r/R=0.7,J=0.806 处的速度分布与实验结果以及面元法的比较[12]。可以看出,在径向速度分布上,CFD 计算值与实验值有良好的一致性,比面元法准确度略高一些;在切向速度分布上,CFD 计算值仍然与实验值保持良好的一致性,特别是在速度峰值处的模拟值要优于面元法;在轴向速度分布上,CFD 计算值虽然与实验值有相似的变化规律,但量值上存在一定的差距,基本满足工程上的应用。本文的CFD 方法虽然数值模拟了粘性的影响,但由于采用的是时均化的RANS 方法,此方法是人为采取的平均化方法,并且引入的湍流方程也是一种近似化的假设。另外,流场中各参量在计算中由于网格间的数据传递而存在耗散现象,因此还无法完全体现出螺旋桨尾流场中尖锐的诱导速度峰值。

图7 径向速度分布Fig.7 Radial velocity distributions

图8 切向速度分布Fig.8 Favorite velocity distributions

图9 轴向速度分布Fig.8 Axle velocity distributions
图10 和图11 分别为x/R=0.295 处截面的轴向速度和横剖面内的速度(径向速度与切向速度的合速度)的分布情况。从中可以清楚地看出尾涡面的位置及周围流场的速度分布,图11 清晰地显示出螺旋桨稍涡的存在。应用CFD 数值模拟,可以直观模拟螺旋桨尾流场,便于对螺旋桨的尾流场进行分析。
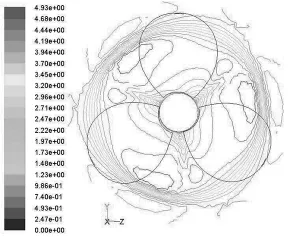
图10 桨后轴向诱导速度Fig.10 Induced axle velocity behind propeller

图11 桨后横向诱导速度分布Fig.11 Induced transverse velocity behind propeller
4 结 语
本文在介绍CFD 概念的基础上,利用CFD 计算方法预报了螺旋桨水动力性能并数值模拟了螺旋桨桨后粘性尾流场。通过对获得的数值结果和试验结果进行比较,得出以下结论:
1)网格质量对CFD 计算精度和计算效率有重要的影响。网格主要分为结构网格和非结构网格。结构网格使用规则单元便于计算,但适用性较差;非结构网格具有良好的灵活性,尤其对复杂问题比较有效,但在计算上相对耗时。因此,一般使用在较简单的几何模型上生成单块结构化网格和多块结构化网格,在复杂几何模型上生成非结构化网格,在结构化网格和非结构化网格之间使用楔形网格过渡的混合网格。并且利用局部加密技术,获取特定位置的精确信息。
2)湍流模型的不同对螺旋桨水动力性能的数值预报存在明显差异。目前几种常用的湍流模型,如标准k-ε 湍流模型、RNG k-ε 湍流模型和SST k-ω模型等都无法完全模拟不同状况下的真实流场,只是在不同应用中有各自的优点。因此,选择合适的湍流模型才能够对螺旋桨的粘性流场进行更准确的数值模拟。
3)近壁面区域处理方式的选取影响数值模拟的结果。对于近壁面区域的处理,Fluent 选用的默认方法实际上是一组半经验公式,用于将壁面上的物理量与湍流核心区域内待求的未知量直接联系起来。这里应该结合网格的壁面精细划分,保证y+值在有效范围内,使流动处于对数律层。
4)发现CFD 对螺旋桨尾流场以及梢涡的形成与结构的数值模拟有较高的准确性,不但能从定性上而且能从定量上预报螺旋桨粘流场。CFD 计算结果与试验结果相比,总的来看吻合较好,采用CFD软件进行的数值模拟结果可以满足工程应用的要求。但也应看到,在细节部分尚存在一定的偏差,在某些位置仍有较大的误差,这都需要在以后的工作中进一步改进与完善。
[1]王福军.计算流体动力学分析——CFD 软件原理与应用[M].北京:清华大学出版社,2004.
[2]STERN F,KIM H,PATEL V C,et al.A viscous-flow approach to the computation of propeller-hull interaction[J].Journal of Ship Research,1988,32(4):246-184.
[3]唐登海,董世汤.船舶螺旋桨周围粘性流场数值预报与流场分析[J].水动力学研究与进展(A),1997,12(4):426-436.
[4]Proceedings of 22ndITTC Propulsion Committee Propeller RANS/PANEL Method Workshop.Grenoble,France,April,1998,5-6.
[5]RHEE S,JOSHI S.CFD validation for a marine propeller using an unstructured mesh based RANS method[C].Proceedings of FEDSM’03,Honolili,USA,2003.
[6]MIKKELSEN R,ANDERSEN P,SORENSEN J N.Modeling of behind condition wake flow in RANS computation on a conventional and high skew propeller[C].Proceedings of 10thNumerical Towing Tank Symposium,Hamburg,Germany,September,2007.
[7]KRASILNIKOV V,SUN J,HALSE K H.CFD investigation in scale effect on propellers with different magnitude of skew in turbulent flow[C].First International Symposium on Marine Propulsors SMP′ 09,Trondheim,Norway,June,2009.
[8]王超,黄胜,常欣,等.基于滑移网格与RNG k-ε 湍流模型的桨舵干扰性能研究[J].船舶力学,2011,15(7):715-721.
WANG Chao,HUANG Sheng,CHANG Xin,et al.Research on the hydrodynamics performance of propeller-rudder interaction based on sliding mesh and RNG k-ε model[J].Journal of Ship Mechanics,2011,15(7):715-721.
[9]苏玉民,黄胜.船舶螺旋桨理论[M].哈尔滨:哈尔滨工程大学出版社,2003.163-169.
[10]JESSUP S D.An experimental investigation of viscous aspects of propeller blade flow[D].Washington:School of Engineering and Architecture,The Catholic University of America,1989.
[11]HOSHINO.Data for the 22ndITTC 98 workshop on panel method and RANS solution[C].Proceedings of the 22ndITTC,Grenoble,France,1998.

