基于屈曲理论的交替支撑塔架计算长度系数的研究

李 靓

（重庆交通大学，重庆 400074）

概述

在结构设计中，要做到安全、经济、合理，除了把握好制作工艺和结构布置以外，还应重视设计分析采用的方法和构造要求。在钢结构设计中重难点就是结构的稳定，而与稳定直接相关的就是计算长度。压杆的计算长度系数μ和计算长度l0，是在材料力学研究压杆稳定性时，引入的一个基本和重要的概念。钢结构设计规范采用的计算长度设计法，其缺点是：只能计算单个构件的稳定，却不能反应结构的整体稳定性；而且由于荷载工况和结构布置的复杂不一性，参照规范规定取值或仅按照一些设计软件默认取值，往往会有较大的误差。

目前研究塔架柱计算长度的文献很少，对于塔架柱平面内的计算长度，规范未做出明确的要求，需要工程师根据实际情况自行分析确定，而解析解往往过于复杂，因此，研究塔架柱计算长度需要采用数值法。本文则立足于计算长度系数的基本概念，通过三种有代表性的计算长度分析方法的比较研究，提出了一种适用于确定塔架柱计算长度的方法。

1 计算模型

文献[2]从三个角度来对柱计算长度确定：整体模型法、独立构件模型法、局部实体有限元分析法。本文在参照以上理论的基础上打算采用三种方法（独立柱子法，归结为方程的特征值问题；一阶弹性分析法，属于第一类稳定问题，在数学上归结为广义特征值问题；二阶弹性分析法，属于第二类稳定问题，在数学上归结为非线性代数方程的求解；直接分析设计法，也归结为非线性代数方程组的求解问题）来确定算例中的柱计算长度系数，并从理论假设和计算结果的角度进行对比分析。

选取的算例为一单柱头万能杆件塔架，塔架节间长度为1m，共3节，底部伸出小节为0.5m。除立柱为4L 120×10角钢外，其余杆件均为2L 75×8角钢，塔架计算模型见图1。

图1 塔架模型

2 独立柱子法

独立柱子模型的分析对象为单独构件，此方法来自材料力学中研究压杆稳定。对塔架计算模型中抽取底端独立柱进行分析，计算简图见图2。根据结构屈曲时存在微小弯曲变形的条件，先建立平衡微分方程，而后求解构件的分叉屈曲荷载。

图2 独立柱模型及计算简图

由文献[3]可知，计算长度系数μ与α(α=a/2b)的关系为：

通过上式即可得到对应不同α时的计算长度系数μ，可知当α=0.25，μ=0.595。

独立柱子法所得的计算长度系数往往偏小，从而高估了结构的稳定承载力。

3 一阶弹性分析法

取整体结构中的单个构件进行独立分析，而忽略其他杆件及支座条件的影响在结构设计中是不可取的。因此需考虑构件之间相互影响，建立整体模型对关键构件进行稳定分析从而体现结构的整体稳定性。在模型中沿构件两端施加一对初始轴向压力（本例中为1000kN），对整体模型进行屈曲分析，可以得到柱第一屈曲模态的临界系数。将此杆件的初始轴力乘以临界系数，即可得到临界荷载Ncr，然后由欧拉公式反算出杆件的计算长度系数。算得临界系数λ=131，故可知Ncr=131×103kN。而欧拉临界力：

从整体结构角度出发，第二个模型中柱计算长度系数将比第一个大，这与计算相吻合。

4 二阶弹性分析法

在结构设计中一阶弹性分析法未考虑结构初始几何缺陷和节点连接刚度等因素的影响，而这些因素是客观存在且对结构稳定的影响不容忽视。如前所述，独立柱子模型和整体线性屈曲模型最终都归结为特征值问题。无变形条件的假定使得特征值模型只能解决分支点失稳问题，而实际结构在各式各样的荷载作用下必然产生变形，有变形结构的失稳问题（极值点失稳）引出本文的第三个计算模型。

采用静力非线性方法对结构进行分级加载，直至结构失稳，对应的极值点即为结构的临界荷载，其位移-荷载变化曲线如图3所示。

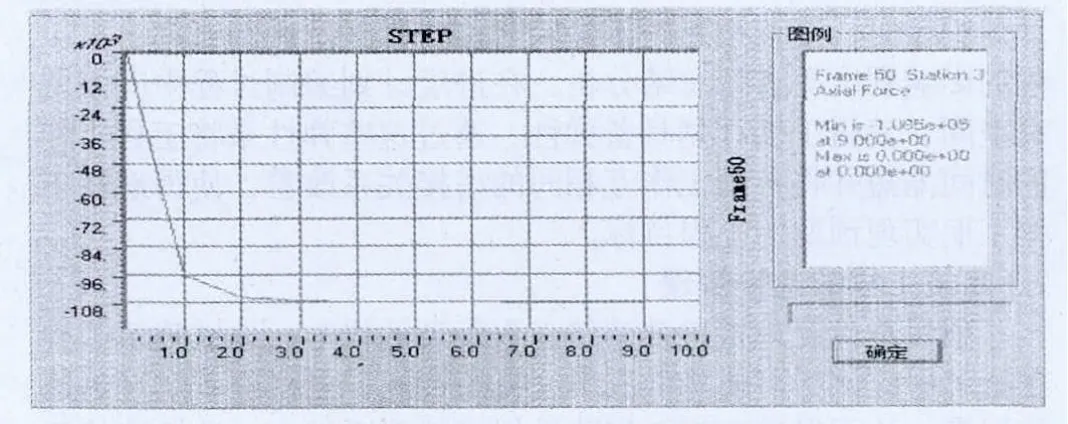
图3 下端柱临界轴力的确定

由图3可知，临界荷载Ncr=1.085×105kN。故

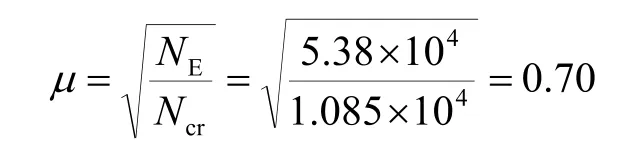
由于考虑了其他荷载作用以及几何非线性的影响，使得柱的临界轴力变小，从而计算长度系数更大了。图4给出了三种分析方法下，随着α改变时对应的计算长度系数μ，计算长度系数μ随着α系数增大而增大，且三种分析方法中二阶弹性分析法更符合实际。

图4 三种分析方法对于不同α时的计算长度系数μ

5 结论

（1）随着α增大，约束作用越来越小，计算长度系数μ变大。

（2）由于一阶弹性分析的力学情况比较简单明确，在数学上作为矩阵特征值问题也比较容易处理，且它的临界荷载可近似代表相应的第二类稳定问题的上限，所以第一类稳定问题在理论分析中仍占有重要地位。

（3）二阶弹性分析真实地反映了结构内各种因素对柱计算长度系数的影响，并且能方便地与结构整体分析、设计过程相结合。与独立柱法、一阶弹性分析相比，非线性所反映出的差异是不容忽视的。现在都用三维建模进行结构设计，它并不比查表慢，不失为一种简单、实用的计算长度确定方法。

[1] GB 50017-2003，钢结构设计规范[S].

[2] 郑竹.利用屈曲分析确定跨层柱计算长度的实用方法[J].四川建筑-工程结构，2009，29（1）：110-112.

[3] 王如新，柳超.输电铁塔中连续轴压杆计算长度系数的讨论[J].长春工程学院学报，2012，13(1).

[4] 李国强.关于多高层钢结构柱计算长度-理论解释[J].建筑钢结构进展，2009，11(2)：1-7.