车种代用情况下的空车调配优化模型及其求解

杨喜娟

（兰州交通大学电子与信息工程学院）

（甘肃省轨道交通装备系统动力学与可靠性重点实验室 （兰州交通大学），甘肃 兰州730070）

张治娟 （甘肃省轨道交通装备系统动力学与可靠性重点实验室 （兰州交通大学），甘肃 兰州730070）

空车调配是铁路运输中的重要组成部分，是指导运输生产的重要手段。由于我国铁路货车大部分是全路通用的，没有固定的配属站，且空车走行公里为非生产走行，不产生运输产品，因而存在空车调配优化的问题［1－4］。为此，笔者建立了车种代作情况下的空车调配优化模型，并应用蚁群算法对其进行了求解。

1 车种代用情况下的空车调配优化模型

设有n个空车供应点Ai（i＝1，2，…，n），供应点对u种空车的供应构成集合节点Ai对u种空车的总供应量为；有r个空车需求点Sj（j＝1，2，…，r），需求点对u种空车的需求构成集合，节点Sj对u种空车的总需求量从Ai到Sj的距离为cij。设空车调整数量决策变量表示由i节点向j节点供应的装运v种货物的u种空车数，≥0且为整数表示j车站待装的v种货物的数量；Quv表示u种空车装v种货物的载重量。针对以上变量，假设所讨论的对象整体是一个封闭的系统，即该系统内所有节点产生的空车的数量与需求的数量是平衡的。

对于空车供应节点i，假设货物的种类为r，发出的空车总数量应与该节点的空车供应量相等，即：

对于空车需求节点，到达的空车总数量应与该节点的空车需求量相等，即：

假设空车产生u种空车数等于空车的需求的u种空车数，即平衡运输，即：

对于空车需求节点j来说，假设空车的种类数为s，对某种货物v的供给能力限制为：

对于u种空车来说，总的走行公里数为：

则所有空车的走行公里数为：

则在平衡情况下，空车调配优化的数学模型如下：：

约束条件为式（1）～（4），其中，u∈U，v∈V，U为空车种类的集合；V为货物种类的集合。

2 应用蚁群算法求解空车调配优化模型

2.1 蚁群算法基本原理

意大利学者M.Dorigo于1991年提出蚁群算法［8］。该算法利用具有记忆功能的人工蚂蚁，通过个体之间相互协作，相互进行信息交流来寻找一条从源节点到目的节点的最短路径。

2.2 用有向图描述空车调配模型

2.3 空车调配优化的算法描述

在求解过程中，若干蚂蚁过程之间通过信息素值来交换信息，合作求解并不断优化，其中信息素值分布式存储在连接图中，与各弧相关联。每只蚂蚁是一个独立的用于构造解的过程，蚂蚁的任务是在约束条件下将所有空车的调配作为一项任务，如果将某一车站供应站的空车种i指派至某一空车需求地的某一物资j，则连接点i与j，同时，在此弧上留下信息素。由于对每个车站的每种物资都指派一项任务，所以，最终的可行解是连接任务与物资的若干条弧。由2个步骤形成完整的解：蚂蚁选择应当被指派的任务；将该任务指派至某一物资，使用弧 （i，j）的信息素以及启发式信息来决定指派的次序，应用局部优化进行信息素更新，在所有的m个蚂蚁都构造完解后，再应用全局信息素更新。下面对求解过程进行描述。

节点间的距离矩阵D＝｛cij｝，T＝｛τij（t）｜i∈K，j∈P｝是t时刻集合G中元素（节点）两两连接边上残留信息量的集合，τij表示t时刻路径（i，j）上的信息素量。在初始时刻各条信息量相等，并设τij（0）＝const。蚂蚁k（k＝1，2，…，m）在运动过程中，根据每条路径上的信息量决定其转移方向。设置二维禁忌表Tuabk（k＝1，2，…，m）和Pslk来记录蚂蚁k当前所经过的节点和配送数量，集合随着Taubk进化过程作动态调整。初始化时将m只蚂蚁随机分配到集合K上，在搜索过程中，蚂蚁根据各条路径上的信息量及路径的启发信息来计算状态转移概率。用pkij表示在t时刻蚂蚁k由节点i转移到节点j的状态转移概率［6］，计算如下：

式中，Taubk中所有元素组成的集合为N，则allowedk＝｛H－N｝表示蚂蚁下一步允许选择的节点，即可选择的节点集合；ηij为空车i转移到物资j的启发信息，取ηij＝1／cij；α为信息启发式因子，表示在路径（i，j）上残留信息的重要程度；β为期望启发式因子，表示启发信息的相对重要性。

在每只蚂蚁配送完一种空车后，调整Taubk和Pslk，并对信息量进行调整，调整规则如下［6］：

在每只蚂蚁把所有的空车都配送完以后，清空Taubk（k＝1，2，…，m）和，准备下一次搜索，并进行全局信息素更新规则，全局更新规则如下：

式中，Lk为最佳路径的长度。

所有蚂蚁重复上述工作直到满足循环条件退出。

3 仿真试验

设空车产生地为s1、s2、s3，空车需求地为t1、t2、t3，空车种类有u1（集装箱平车 XN17）、u2（敞车C64）、u3（棚车P64GK），货物种类有v1（粮食）、v2（木材）。则有u3装v1、u2装v2、u1和u2可代装v1、u1可代装v2。空车供给表、货物供给表、货车标记载重和装运货物品类重量表以及运输距离表如表1～4所示。

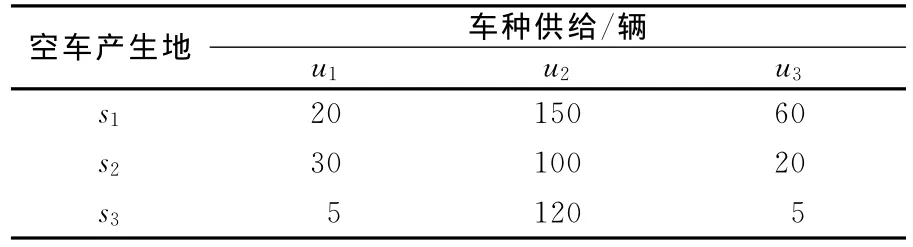
表1 空车供给表

表2 货物供给表

表3 货车标记载重和装运货物品类重量表

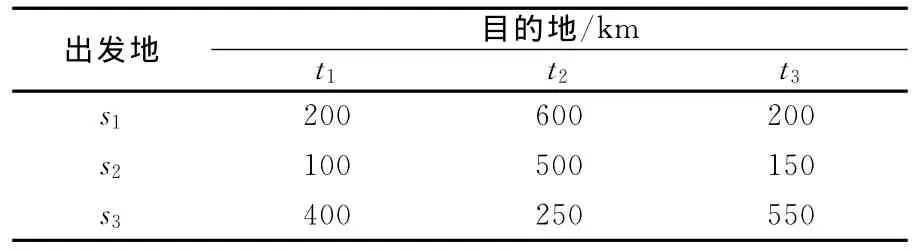
表4 运输距离表

采用蚁群算法求解上述问题，首先代入约束条件和目标函数，再使用Matlab7.0对算例进行求解，使用的参数为m＝15；ρ＝0.2；α＝2；β＝4；NC max＝200；Q＝10000。在仿真过程中连续计算20次，具体计算结果如表5所示。

表5 利用蚁群算法连续进行20次计算的统计结果表

从表5可以看出，使用蚁群算法求解车种代用下的空车调配模型具有得到最优解的比率高、平均解相对误差低、最优解的收敛速度较快等优点，能很好地解决空车产生总数和空车需求总数相等的平衡运输问题。