液体比热容实验的温度设定及实验不确定度的理论分析

卢贵武，韩志强，郑 超，张 鹏

（中国石油大学（北京）理学院，北京102249）

1 引 言

物质的比热容是表征其热学性质的重要物理量，在许多的高校大学物理实验课中都开设了关于固体、液体和气体比热测量的实验项目，根据实验的目的、要求、仪器等设计成基础实验、设计性实验和综合实验［1-8］，采用了各种方法对物质的比热容进行测量.在液体比热的测量中电热法是常用的方法，在实验中往往采用对称测量法来消除量热器与环境热交换的影响.然而在对称测量法测比热过程中，由于系统温度高于室温时升温较慢，系统温度低于室温时升温较快，因此整个实验过程中系统对外界放出的热量大于从外界吸收的热量，导致测得的比热值偏大.显然，若能合理地设定末温T2，使系统从外界吸收的热量接近向外界放出的热量，则可真正地消除系统与外界的热交换对实验结果的影响.储浚［9］和阎向宏［10］等人曾采用牛顿冷却定律分析讨论了对称测量方法对实验结果的影响，提出了提高实验准确度的建议.本文采用气体热传导理论定量研究了温度对“电热法测定液体比热容”实验结果的影响.

2 模型与理论分析

传统的“电热法测定液体的比热容”的实验装置如图1所示.假设内筒壁的温度为样品温度T，外筒壁的温度为环境温度T0，样品与环境的距离为L，上述装置可简化为图2.

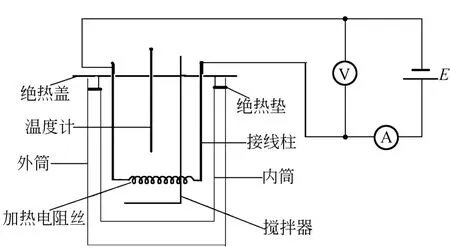
图1 实验装置图

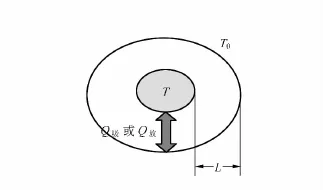
图2 热传导模型图

设温度梯度在径向分布均匀，依据气体热传导理论，样品与环境之间的热流j（即单位时间内流过单位面积的热量）可表述为

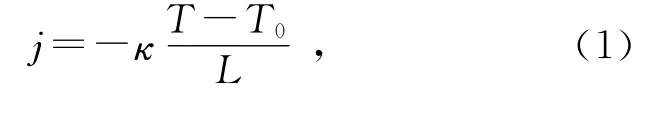
式中，κ为空气热导率，T为样品温度，T0为环境温度，L为样品与环境间的距离.

在实验的前期阶段，温度从T1经过时间t1升高到T0，系统从环境中吸取热量.在单位时间内，系统从外界吸取的热量为

式中，S为样品与环境的接触面积.在dt时间内，温度升高dT，则有：

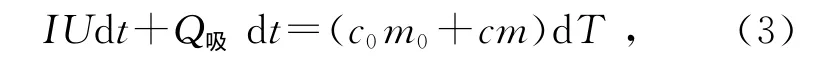
式中，IU是电阻丝的发热功率，c0和c分别是内筒（附加电阻丝、接线柱和搅拌器）和样品的比热容，其质量分别为m0和m.将（2）式代入（3）式得

令：

则得到时间和温度的关系式为

对（6）式积分得到吸热过程的持续时间为

在吸热过程中系统从环境中吸取的总能量为

在实验的后期阶段，温度由T0上升到T2，系统向环境释放热量.在单位时间内，系统向环境释放的热量为

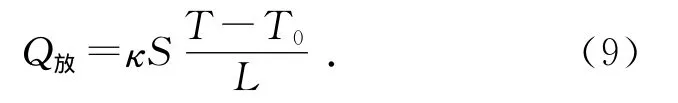
在dt时间内，系统温度升高dT，则

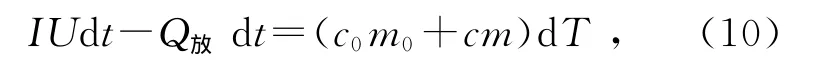
对（10）式积分得到放热过程持续时间为

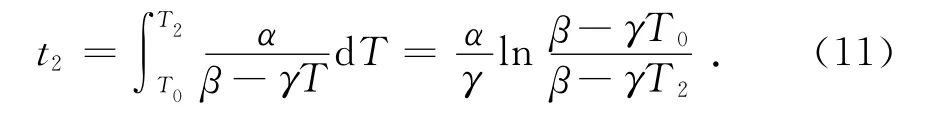
在放热的过程中，系统向环境中释放的总热量为：

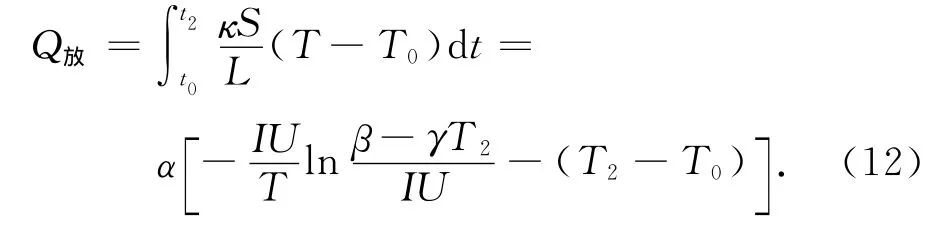
在整个实验过程中，为减少系统与环境温度间的热交换对实验的影响，需令系统吸收的总热量与释放的总热量相等（Q吸＝Q放），由（5），（8）及（12）式得到：

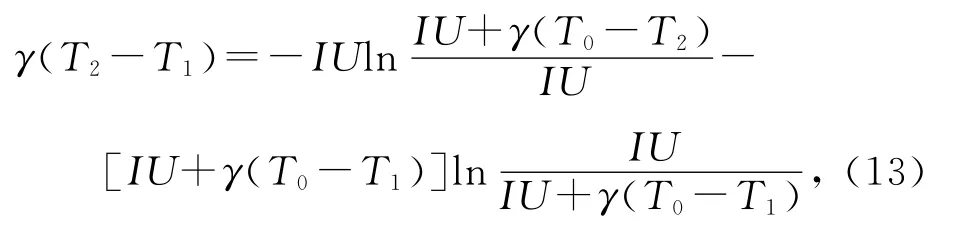
该式为设定实验终止温度的基本公式.

3 实验结果与讨论

待测液体为煤油，质量m＝136.1g，量热器内筒、搅拌器、加热电阻丝和接线柱的质量m0＝145.1g，比热容c0＝385.2J／（kg·K）.取T0＝17.8℃，T1＝13.5℃，加热电阻丝的电压U＝6.22V，电流I＝0.355A，实验测得从初始温度到室温的加热时间t1＝600s.

将以上数据代入（7）式并令煤油比热容c＝2.14×103J／（kg·K），可求得

代入式（13）得到T2＝21.2℃，与采用对称法（T2-T0＝T0-T）得到的T2（为22.1℃）相比，设定的温度低了0.9℃.

依据上述数据，由（11）式得到系统从室温T0升高到一定温度T所需要的加热时间t2与温度T的关系曲线如图3所示.此曲线显示，随着温度的提高，所需要的加热时间呈指数式增长.当T＝31.5℃时，所需要的加热时间趋于无穷大，也就是说此时加热器提供的能量与向环境释放的热量相等，系统的温度稳定在31.5℃.

图3 系统从室温T0升高到一定温度T所需要的加热时间t2与温度T的关系曲线

对于整个实验过程，有（5）式成立：

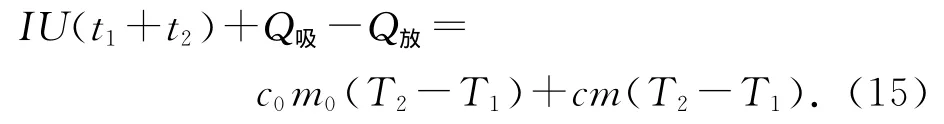
由式（5）～（15）得

此为液体比热容c与终止温度T2之间的关系.由此可得终止温度T2的不确定度传递系数为

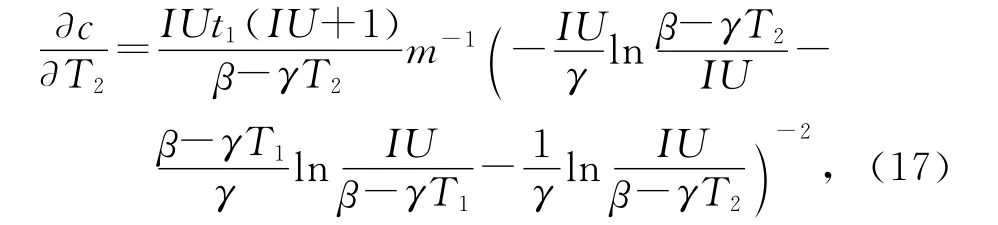
取ΔT＝0.9℃，由（17）式可得到比热c的不确定度为

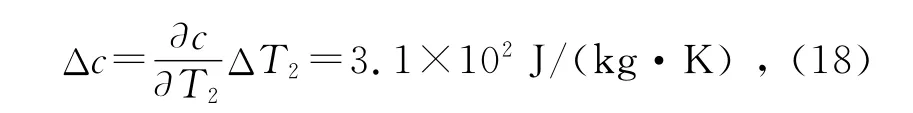
液体比热容c的相对不确定度为

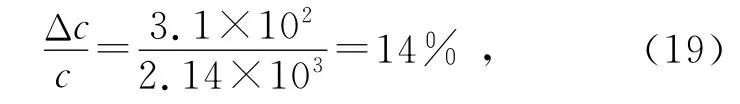
这一结果表明，我们的温度设定新方法可减少实验相对不确定度14%.

测量系统从室温T0升高到一定温度T所需要的加热时间t，得到t与温度T的实验结果如表1所示.取T2＝22.1℃，实验测量的比热c＝2.47×103J／（kg·K），与参考值2.14×103J／（kg·K）比较，实验的相对不确定度为15.4%；取T2＝21.2℃，实验测量的比热c＝2.12×103J／（kg·K），实验的相对不确定度为0.9%；表明我们的温度设定显著地提高了实验精度.

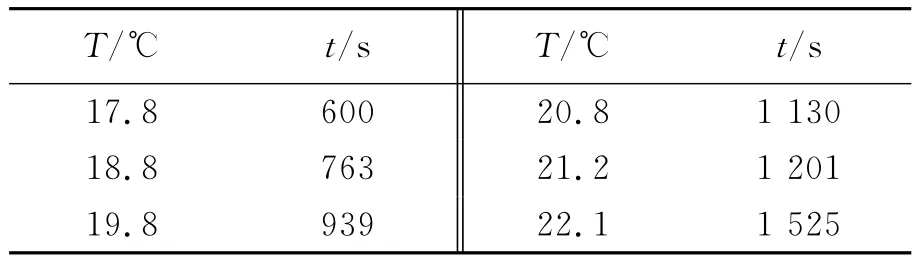
表1 系统从室温T0升高到温度T对应的加热时间t

4 结 论

依据热传导理论推导了加热时间与终止温度的关系，提出了可显著提高实验准确度的温度设定方法.具体数值计算表明，为了减少环境热量交换对实验结果的影响，实验的终止温度应比传统方法设计的温度降低0.9℃；采用新的温度设定方法，提高了实验精度.应指出本文为了简化计算假定系统与环境之间温度梯度的径向分布与位置无关，进一步的理论分析应考虑环境温度变化对结果的影响、热量的径向传输对温度梯度的影响以及温度对气体热导率的影响.

［1］张文杰.温度传感器在固体比热容实验中的运用［J］.物理实验，2012，32（8）：21-23.

［2］常相辉，冯先富，张永文，等.不同温度下空气比热容比测量装置的研究［J］.物理实验，2011，31（4）：21-23.

［3］王银峰，陶纯匡，汪涛.大学物理实验［M］.北京：机械工业出版社，2005.

［4］秦仙明.大学物理实验［M］.北京：石油工业出版社，2007.

［5］唐海燕.大学物理实验［M］.北京：高等教育出版社，2011.

［6］朱世坤，辛旭平，聂宜珍，等.设计创新型物理实验导论［M］.北京：科学出版社，2010.

［7］孙为，唐军杰，王爱军，等.大学物理实验［M］.北京：中国石油大学出版社，2007.

［8］周开学.工科大学普通物理实验［M］.东营：石油大学出版社，1991.

［9］储俊.电热法测液体比热实验中量热器散热的修正［J］.物理实验，1995，15（3）：107-108.

［10］阎向宏，张亚萍.电热法测液体比热容实验的改进［J］.大学物理实验，1997，16（7）：23-24.