花岗岩残积土邓肯-张模型参数的合理确定
赖榕洲,吴能森,徐 青
(福建农林大学 交通与土木工程学院,福建 福州 350002)
花岗岩残积土邓肯-张模型参数的合理确定
赖榕洲,吴能森,徐 青
(福建农林大学 交通与土木工程学院,福建 福州 350002)
为合理确定花岗岩残积土的邓肯-张模型参数,制作3种不同含水率的试样,分别在围压100 kPa、200 kPa和300 kPa条件下进行固结排水三轴试验,得到的应力~应变关系曲线均呈非线性加工硬化型,符合邓肯-张模型的适用条件。然后分别采用“全点法”和“两点法”求取邓肯-张模型参数,并利用求取结果对模型曲线进行拟合,结果表明:“全点法”因不可避免要受到异常数据的干扰,所求取模型参数精度较低,而“两点法”仅使用高应力水平的两组数据,不仅简单、方便,且可以避免低应力阶段异常数据的干扰,所求取模型参数精度较高。建议工程上采用“两点法”确定花岗岩残积土的邓肯-张模型参数。
花岗岩残积土;邓肯-张模型;三轴试验;全点法;两点法
花岗岩残积土是花岗岩经过物理风化和化学风化后残留在原地的碎屑物,具有特殊的成分和结构特征,属区域性特殊土,在我国南方分布广泛。[1]邓肯-张模型能较好地反映土体的非线性,且概念清晰,模型参数明确易得,便于工程应用。[2]在岩土及地下工程分析计算中,需要具体的邓肯-张模型参数值,在土体本构模型适用的前提下,其模型参数的精确性决定了分析计算结果的可靠性。[3]为此,拟对花岗岩残积土进行常规三轴试验,应用两种不同方法求取邓肯-张模型的参数值,并通过拟合曲线和试验曲线的对比,分析两种方法的精确性,据此提出合理确定花岗岩残积土邓肯-张模型参数的建议。
1 邓肯-张模型简介
1963年,康纳(Kondner)[4]在大量三轴试验基础上,提出围压为常数的常规三轴固结试验的加工硬化型应力~应变关系可近似地用双曲线来表示,即:

(1)
式中,a、b为试验常数,ε1为轴向应变,σ3为围压,σ1为轴向主应力。
可将式(1)改写为:
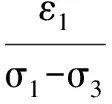
(2)
式(2)是一直线方程,a、b分别为该直线的截距、斜率,可通过试验数据拟合直线获得。
1970年,邓肯(Duncan)和张(Chang)等[5]根据式(1)提出了包括切线模量Et和切线泊松比μt的邓肯-张本构方程式,简称邓肯-张模型E-μ模型,其中切线模量Et表达式为:
(3)

(4)
式中:Ei为初始切线模量(kPa),c为土的粘聚力(kPa),φ为土的内摩擦角(°),Rf为破坏应力比,K、n为试验常数,Pa为大气压力(取101.4 kPa)。
Ei、Rf与a、b的关系为:
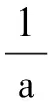
(5)
Rf=b(σ1-σ3)f
(6)
式中,(σ1-σ3)f为土样破坏时的偏应力。
将式(4)进行坐标变换,可变为lgEi~lgσ3直线,则该直线斜率为n,当lgσ3=1时的lgEi值即为lgK。
在邓肯-张模型的计算中,常用应力水平S来衡量土体强度发挥的程度:

(7)
式中各变量意义同上。
2 试验概况
试验土样取自福州晋安区鹤林新城二区某地块,取土深度12.3~16.8 m,土样呈褐黄、肉红色,硬塑状态,原状土含水率ω=30.1%,密度ρ=1.84 g/cm3,土粒相对密度ds=2.72。试验仪器为SLB-1型应力~应变控制式三轴剪切渗透试验仪,采用固结排水三轴压缩试验(CD试验)[6]。土样经风干、碾碎、过孔径为2 mm筛后,分别取含水率13%、17%、21%,按击实法制备试样,试样直径39.1 mm,高80 mm。试验固结围压σ3分别取100 kPa、200 kPa、300 kPa,当体积读数变化微小或长时间保持不变时认为试样完成固结。固结完成后,在围压σ3保持不变的情况下,采用应变控制方式,以0.012%/min剪切速率增加轴向压力进行排水剪切,直至试样轴向应变值达到15%时停止试验,试验过程中排水阀始终保持开启状态。
试验数据及相关曲线由仪器自动采集和绘制,如试样的主应力差(σ1-σ3)与轴向应变ε1关系曲线(图1)。
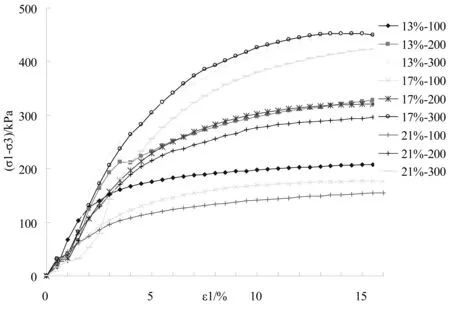
图1 (σ1﹣σ3)~ε1关系曲线 Fig.1 The curves of (σ1﹣σ3)~ε1

图2 三轴剪切摩尔强度包线Fig.2 The Mohr strength envelope of triaxial test
3 邓肯-张模型参数确定
由图1可见,花岗岩残积土试样的应力~应变曲线总体上呈非线性的加工硬化型,与邓肯-张模型的条件式(1)基本吻合,但在小应变阶段试验数据大多不太正常。式(3)~(6)中共有5个模型参数,即c、φ、K、n、Rf,其中c、φ值按摩尔库伦准则,根据围压σ3和破坏偏应力(σ1-σ3)f绘制强度包线获得(图2)。由图2得:含水率13%时c、φ值分别为24.88 kPa、24.1°;含水率17%时c、φ值分别为18.51 kPa、23.9°;含水率21%时c、φ值分别为8.69 kPa、23.5°。模型参数K、n、Rf大小取决于试验常数a、b,下面分别采用“全点法”和“两点法”确定a、b值,然后进行比较分析。
3.1“全点法”求取。
所谓“全点法”就是将全部的(σ1-σ3)~ε1试验数据,按式(2)进行线性化处理,并绘制拟合直线求得a、b值。将全部试验数据线性化后得到散点图,如图3所示,可见除了在轴向应变较小(基本在3%以内)时,有一些散点分布异常、与理论位置偏差巨大外,同一试验的其他散点基本分布在一条直线上。根据图3所拟合的直线(略),可确定“全点法”的试验常数a、b及模型参数K、n、Rf,见表1。
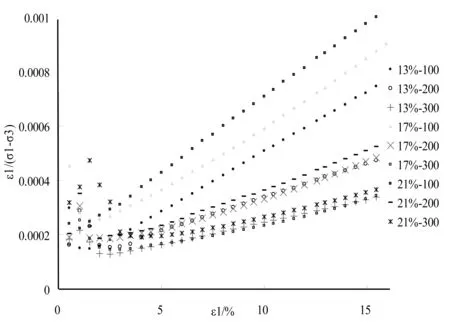
图3 “全点法”线性化散点图 Fig.3 The linearization scatter plot of “All point method”
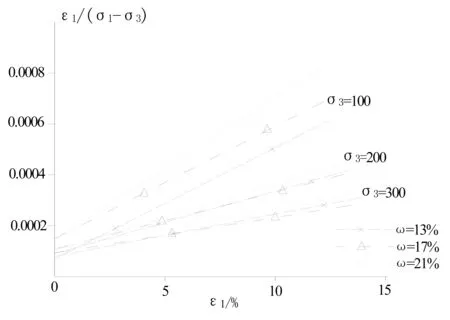
图4 “两点法”直线Fig.4 The straight line of “Two point method”
3.2“两点法”求取。
所谓“两点法”是提取应力水平S=70%和S=95%的线性化试验数据,在ε1/(σ1-σ3)~ε1坐标系中作通过该两点的直线,从而求得a、b值[7]。根据试验数据所作的“两点法”直线如图4所示,依此求得的a、b值及模型参数K、n、Rf也列在表1中。
3.3 模型曲线拟合。
根据上述两种方法得到的试验常数a、b,按式(1)采用Matlab拟合出各试样在不同围压下的应力~应变曲线,并与试验曲线进行对比,如图5所示。可见,除个别情况外,两种方法在小应变时的拟合结果比较接近,但当轴向应变达到一定值后,“两点法”的拟合曲线大部分几乎和试验曲线重合,而绝大多数“全点法”的拟合曲线明显低于试验曲线,因此“两点法”的拟合精度明显高于“全点法”。

表1 邓肯-张模型参数及试验常数对照表
从表1分析,“全点法”拟合结果总体偏小的原因是试验常数b偏大。b值偏大,意味着偏应力的极限值(σ1-σ3)ult偏小,导致破坏应力比Rf偏大。再进一步究其原因,是由于受试验的系统误差及试验操作等人为因素的影响,各试样在低应力阶段的应力应变关系均存在不同程度的异常。由于“全点法”使用了全部试验数据,不可避免要受这些异常数据的干扰而影响精度,而“两点法”仅使用高应力水平的两组数据,不仅简单、方便,而且避免了低应力阶段异常数据的干扰。

图5 应力~应变曲线拟合
4 结语
为了提高岩土及地下工程分析计算的可靠度,除了所选用的岩土本构模型必须比较符合实际外, 关键在于计算
所用的模型参数的精度。研究表明,花岗岩残积土的应力应变关系与邓肯-张模型基本吻合,适宜使用邓肯-张模型进行分析计算,但由于受试验的系统误差及试验操作等人为因素的影响,试验数据在低应力阶段通常存在异常现象,因此若采用“全点法”确定模型参数,不可避免要受到异常数据的干扰而影响精度,而“两点法”仅使用高应力水平的两组数据,不仅简单、方便,而且可以避免低应力阶段异常数据的干扰,精度较高。为此建议采用“两点法”确定花岗岩残积土的邓肯-张模型参数。
[1]吴能森,赵尘,侯伟生.花岗岩残积土的成因、分布及工程特性研究[J] .平顶山工学院学报,2004,13(4):1-4.
[2]张学言,闫澍旺.岩土塑性力学基础(第2版)[M].天津:天津大学出版社,2004:60-65.
[3]徐中华,王卫东.敏感环境下基坑数值分析中土体本构模型的选择[J].岩土力学,2010,31(1):258-264.
[4]Kondner R L. Hyperbolic Stress-stain Response: Cohesive soils [J].Journal of the Soil Mechanics and Foundations Division. ASCE, 1963, 89( SM1): 115-143.
[5]Duncan J M, Chang C Y. Nonlinear analysis of Stress and Strain in Soils [J].Journal of the Soil Mechanics and Foundations Division. ASCE, 1970, 96(SM5): 1629-1653.
[6]GB/T 50123-1999 土工试验方法标准[S].
[7]冯卫星,常绍东,胡万毅.北京细砂土邓肯-张模型参数试验研究[J].岩土力学与工程学报,1999,18(3):327-330.
ClassNo.:TU411DocumentMark:A
(责任编辑:宋瑞斌)
ReasonablyDeterminingtheParametersofDuncan-ChangModelforGraniteResidualSoil
Lai Rongzhou, Wu Nengsen, Xu Qing
(School of Transportation and Civil Engineering, Fujian Agriculture and Forestry University, Fuzhou, Fujian 350002,China)
To determine Duncan-Chang model’s parameters of granite residual soil, three different moisture content samples were made and triaxial consolidation drained tests were done under surrounding pressures of 100 kPa、200 kPa and 300 kPa respectively. All stress-strain curves obtained are of the property of work-hardening which coincides with the conditional formula of Duncan-Chang model essentially. Afterwards, parameters of Duncan-Chang model were calculated to curve fit by means of “all point method” and “two point method” respectively, and the result is as follow: “all point method” is poor than “two point method” in accuracy, because “all point method” is interfered by abnormal data unavoidably; whereas “two point method” is not only simple and convenient, but can prevent from being disturbed by abnormal data in low stress level due to only using two sets of data in high stress level, so, It is suggested that “two point method” should be apply to calculate the Duncan-Chang model’s parameters of granite residual soil in engineering practice.
granite residual soil;Duncan-Chang model; triaxial test; all point method; two point method
赖榕洲,硕士,福建农林大学交通与土木工程学院。
吴能森,通讯作者,博士,教授,博士生导师,福建农林大学交通与土木工程学院。研究方向:岩土力学及地下工程。
福建省自然科学基金项目(2007J0357);福建省高等学校科技项目(JA09073);福州大学土木工程国家级实验教学中心第三期创新性实验研究项目(IRP2012-3);福建农林大学创新(培育)团队建设项目(Pytd12006)。
1672-6758(2013)12-0071-3
TU411
A

