基于偏最小二乘回归的城镇登记失业率预测*
韩庆艳 李文涛
(1.安徽邮电职业技术学院 合肥 230031)(2.陆军军官学院 合肥 230031)
1 引言
失业率是反应社会形态的重要指标,是国民经济中极其重要的问题。近年来,国外学者非常关注城镇失业率预测问题[1~3],我国的向东进[4]、向小东[5]、杨帅国[6]、曹灿[7]等从不同角度,采用各种方法对城镇失业率进行了预测,取得了较好的效果。但是,从这些文献中可以看出,为了完备地描述这一问题,分析人员尽可能多地选取影响城镇失业率的因素,在城镇失业率预测系统中往往会出现影响因素多重共线现象。王惠文在文献[8]指出,无视这种多重共线性,会影响分析的客观性,使结果产生严重偏差。
偏 最 小 二 乘 回 归[9~10](Partial Least-Squares Regression,PLSR)是一种新型的多元统计分析方法,集多元线性回归、典型相关分析和主成分分析的功能为一体,能有效解决自变量因子间的多重共线性影响的问题,因此,本文拟对PLSR建模方法在城镇失业率预测中的应用加以探讨,以提高模型拟合效果和预测精度。
2 城镇登记失业率影响因素与多重共线性诊断
2.1 城镇登记失业率影响因素分析
失业的统计方法各国差异较大,我国采用城镇登记失业率,是指城镇登记失业人数同城镇从业人数与城镇登记失业人数之和的比。其中,城镇登记失业人员是指有非农业户口,在一定的劳动年龄内(16岁以上及男50岁以下、女45岁以下),有劳动能力,无业而要求就业,并在当地就业服务机构进行求职登记的人员[11]。
通过查阅相关资料,选取劳动力因素、国家政策类因素、居民消费类因素、投资与经济类因素和产能结构因素等五类影响因素,具体指标包括:
1)劳动力因素类,包括年度总人口、经济活动人口、城镇就业人员数、城镇单位就业人口平均工资、城镇单位劳动人员就业总报酬。
2)国家政策因素类,包括教育经费投入和财政支出。
3)居民消费因素类,包括居民消费价格指数(CPI)增长率、最终消费支出以及社会消费品零售总额。
4)投资和经济因素类,包括进出口总额、城镇固定资产投资、GDP、GDP增长率、汇率等。
5)产能结构因素类,包括第一产业、第二产业和第三产业的产值比重。
综上所述,得出了影响城镇登记失业率的五大因素和18个指标,并且给出了结构框架表,如表1所示。

表1 城镇登记失业率影响因素和指标结构图
2.2 影响因素多重共线性诊断
选定的城镇登记失业率影响因素有18个,可能将存在一些近似线性的变量选作解释变量,这种解释变量间的近似线性关系在统计中称之为多重共线性(multicollinearity)[12]。由于多重共线性的存在,违背了线性回归模型的假定,使得具有良好特性的最小二乘估计与最小二乘理论遭到严重破坏,所作的预测也就完全失效。因此有必要进行多重共线性诊断。
目前较为常用的诊断方法主要有:条件指标法、特征分解法、方差扩大因子法、本征值与病态指数检验法等。本文采用本征值与病态指数检验法[13~14]。
该检验法是由贝尔斯等人1980年提出的。首先对影响因素矩阵X中心化、标准化,再计算出R-1=(X′X)-1,设λmax与λmin为R-1的最大本征值和最小本征值,设k为病态数,定义为k=λmax/λmin,病态指数CI定义为
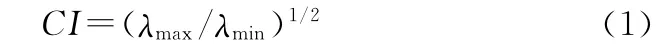
根据经验,如果k∈[100,1000],则认为有中度多重共线性,如果k>1000,则认为存在严重的多重共线性;如果CI∈[10,30],则认为有中度多重共线性,如果CI>30,则认为存在严重的多重共线性。
利用该方法,对影响因素数据进行计算得:λmax=180.52与λmin=3.2219×10-2,代入式(1)得:k=5602.9,CI=74.8526,说明在18个影响因素之间存在着严重的多重共线性。
3 偏最小二乘回归与算法
3.1 偏最小二乘回归
考虑p个变量y1,y2,y3,…,yp与m 个自变量x1,x2,x3,…,xm的建模问题。偏最小二乘回归的基本作法是首先在自变量集中提取第一成分t1,同时在因变量集中也提取第一成分u1,并要求t1与u1相关程度达到最大。然后建立因变量y1,y2,y3,…,yp,与t1的回归,如果回归方程已达到满意的精度,则算法中止。否则继续第二对成分的提取,直到能达到满意的精度为止。若最终对自变量集提取r个成分t1,t2,t3,…,tr,偏最小二乘回归将通过建立y1,y2,y3,…,yp与t1,t2,t3,…,tr的回归式,然后再表示为y1,y2,y3,…,yp与原自变量x1,x2,x3,…,xm的回归方程式,即偏最小二乘回归方程式。
为了方便起见,不妨假定p个因变量y1,y2,y3,…,yp与m个自变量均为标准化变量。因变量组和自变量组的n次标准化观测数据阵分别记为
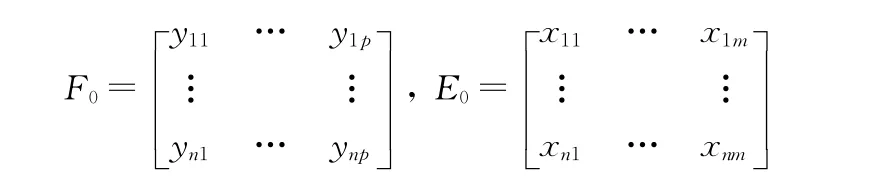
3.2 偏最小二乘法回归的简洁算法
偏最小二乘法的简洁算法的步骤如下:


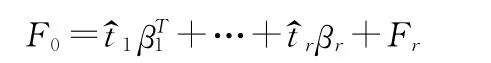
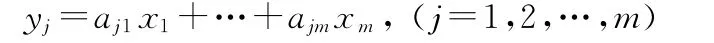
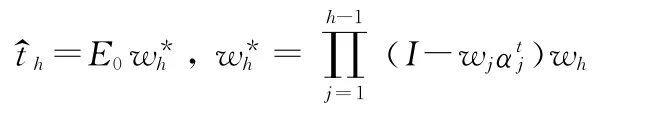
4 基于PLSR模型的我国城镇登记失业率预测
4.1 模型建立
根据中国统计年鉴中的统计数据,并查阅相关资料,得出1997~2011年间这18个指标和城镇登记失业率的数据,按照3.2中的偏最小二乘法回归算法,采用Matlab程序编程[15],通过程序运算得我国城镇登记失业率的偏最小二乘回归模型为

4.2 交叉有效性变量累计解释能力
偏最小二乘回归方程并不需要选用全部的成分进行回归建模,而是与主成分分析一样,采用截尾的方式选择几个成分就可以得到一个预测性能较好的模型。对于因变量y,成分th的交叉有效性为,经计算交叉有效性如表2所示。

表2 成分th对因变量y的交叉有效性
4.3 变量累计解释能力
根据交叉有效性计算结果,从自变量系统中提取了五个成分,由成分对变量解释能力定义,计算成分th(h=1,2,3,4,5)对自变量X和因变量y的累计解释能力,如表3所示。
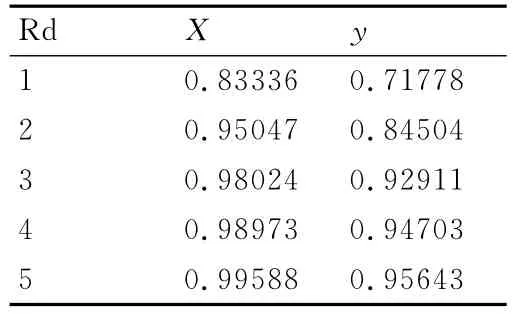
表3 成分th(h=1,2,3,4,5)的解释能力
从表3可见,提取五个成分时,对的X累计解释能力达到99.6%,对y的累计解释能力达到96%,自变量系统与因变量系统相关性较高。
4.4 预测结果与误差分析
根据式(2)中的偏最小回归方程,将数据代入计算得拟合值,并进行误差分析,结果如表4所示。
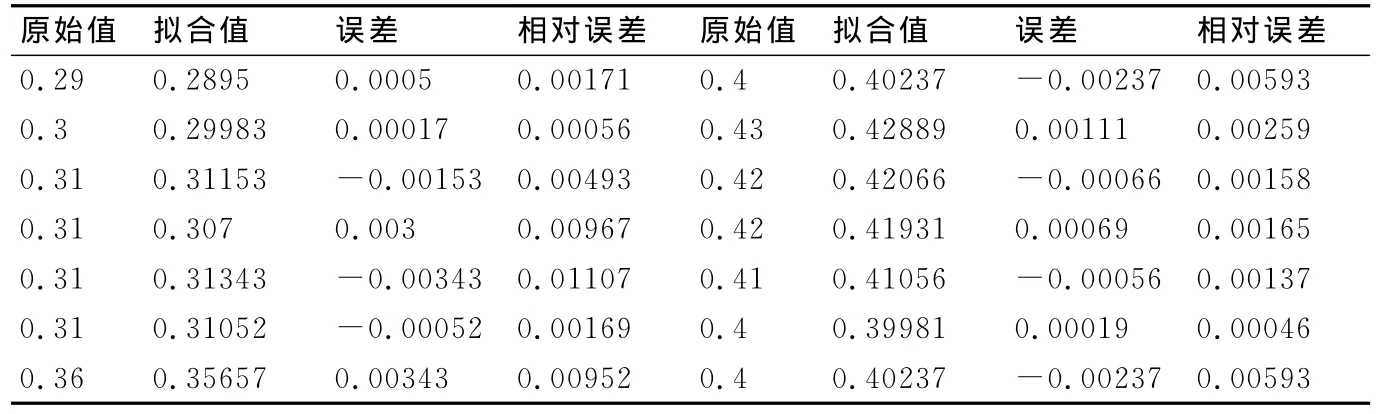
表4 城镇登记失业率预测/拟合误差对比表
根据数据绘制了预测/实际值对比图和误差分析图,如图1、图2所示。
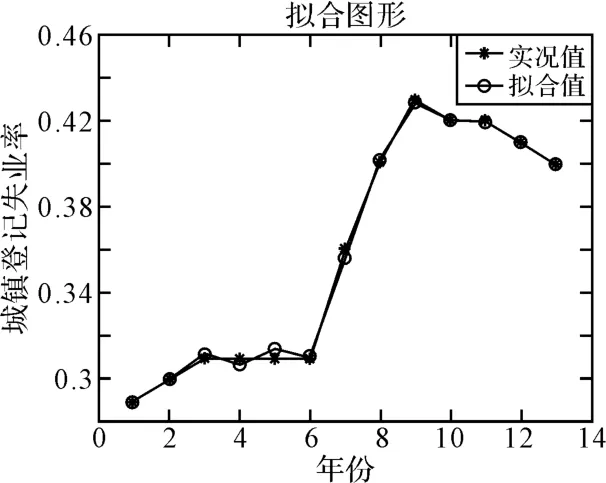
图1 预测/实际值对比图

图2 误差分析图
从以上图表的计算结果可以看出,偏最小二乘回归模型的预测误差为-0.00343,最大相对误差为0.01107,预测精度高,拟合效果较好,
5 结语
本文根据以往研究,总结出了城镇登记失业率的五类影响因素:劳动力因素、国家政策类因素、居民消费类因素、投资与经济类因素和产能结构因素和18个预测指标,采用本征值与病态指数检验法进行多重共线性进行诊断,说明在18个影响因素之间存在着严重的多重共线性。为了克服多重共线性导致的预测失真问题,运用偏最小二乘回归模型,以我国城镇登记失业率为研究对象,按照Q2h≥0.0975的决策原则,由于Q24=0.2501,而Q25<0,提取5个主成分时,对的X累计解释能力达到99.6%,对y的累计解释能力达到96%,方程的预测性能为最佳,自变量系统与因变量系统相关性较高。该方法还可以进一步推广到类似问题的解决中去。
[1]Chen,chun-I.Application of the novel nonlinear grey Bernoulli model for forecasting unemployment rent[J].Chaos,Solitons and Fractals,2008(37):278-287.
[2]Proietti,Tommaso.Forecasting the US unemployment rate[J].Statistics and Data Analysis,2003(42):451-476.
[3]Chiu,Chih-chou,Su,chao-ton.Novel neural network model using Box-Jenkins technique and response surface methodology to predict unemployment rate[J].Proceeding of the International Conference on Tools with Artificial Intelligence,1998(23):74-80.
[4]向东进,范辉.我国城镇登记失业率的影响因素分析及预测[J].湘潭大学学报,2010(5):73-77.
[5]向小东,宋芳.基于核主成分与加权支持向量机的福建省城镇登记失业率预测[J].系统工程理论与实践,2009(1):73-79.
[6]杨帅国,胡晓华,朱冬和.我国城镇登记失业率的数学模型与预测[J].海南师范大学学报,2010(4):372-374.
[7]曹灿,赵联文.基于多元回归分析中的中国城镇失业率问题研究[J].长春大学学报,2011(4):50-53.
[8]王惠文.偏最小二乘回归方法及其应用[M].北京:国防工业出版社,1999:65-97.
[9]Erikson L,Johansson E,Kettaneh W N,et al.Mutiple and mega variate data analysis:Principles and applications[M].umea:umetrics,2001:84-104.
[10]Schreiber T.Extremely simple nonlinear noise reduction method[J].Phys Rev E,1993(47):2401-2405.
[11]张车伟.失业率定义的国际比较及中国城镇失业率[J].世界经济,2003(5):73-76.
[12]Moore,William L.A cross-validity comparision of ratingbased and choice-based conjoint analysis models[J].International Journal of Research in Marketing,2004(3):299-312.
[13]高辉.多重共线性的诊断方法[J].统计与信息论坛,2003(1):73-76.
[14]赵松山,白雪梅.关于多重共线性检验方法的研究[J].中国煤炭经济学院学报,2001(4):296-300.
[15]周品,赵新芬.Matlab数理统计分析[M].北京:国防工业出版社,2009:103-126.

