数据挖掘技术在中、高职关键能力衔接指标构建中的应用*

王茂莉

（深圳职业技术学院，广东 深圳 518055）

关键能力是一种独立于具体的专业能力以外的能力，是一种从事任何职业的劳动者都应具备，能够在变化的环境中重新获得新的职业知识和技能的能力，在未来职业活动中发挥重要作用的内在品质和外在行为方式，更是应对人生生涯中不可预见的各种变化的能力．此项能力是可持续发展的关键．中高职衔接既是一种现实的、符合实际的中职教育与高职教育的衔接模式，又是一条高技能人才培养的有效路径．中、高等职业教育在内部互相联系的同时，与社会、行业和企业也密切相联．作为同为行业企业及社会培养生产一线技术技能型人才的职业教育培养，他们存在着专业上的贯通性；作为实用型和应用型人才的中等和高等职业教育，更存在着“关键能力”培养上的一致性．所以，中高等职业教育衔接培养，不仅是专业能力上的衔接，更应强调关键能力上的贯穿．

1 数据挖掘技术研究

数据挖掘DM（Data Mining）就是从大量不完全、有噪声、模糊、随机的实际采集数据中，提取隐含在其中的有用的信息和知识的过程．简言之，是从特定形式、纷繁复杂的数据中集中提炼知识的过程．数据挖掘过程包括数据采集、数据处理、数据变换、数据挖掘、模式评估、知识表示等，其中有些步骤或者全过程可能要反复进行．数据挖掘的方法较多，常见的有关联规则的挖掘、层次分析法、决策树方法、神经网络方法、覆盖正例排斥反例方法、粗糙集方法、遗传算法、公式发现、统计分析方法、模糊论方法、可视化技术等[1]．

层次分析法（Analytic Hierarchy Process，AHP）是由美国运筹学家T．L．Saaty教授提出的，是针对定性问题进行定量分析的一种简便、灵活又实用的多准则决策方法．它把一个复杂问题分解成组成因素，并按支配关系形成层次结构，然后应用两两比较的方法确定决策方案的相对重要性[2]．特别是，它为评价问题提供一种建模方法，将评价系统从无结构转化为结构化；将半定性、半定量的问题转化为定量计算的问题，从而解决多目标、多准则等各类型问题的决策分析过程，具有广泛的实用性．

2 AHP算法在中高职学生关键能力指标体系权重分析中的应用

2.1 构建评价指标层次结构模型

对于中、高职学生，其在专业能力上的要求具有递进性，而在对其关键能力的培养上，则具有共通性．关键能力的理念在不同的国家有不同的内涵诠释，见表1．

从各国定义的关键能力可以看出，学习能力、社会能力、语言能力、规划与组织能力、运用技术能力等能力是多数国家都认可的能力．而通过第三方调查公司的调查数据显示，在2010届高职院校毕业生的调查中，学生对“关键能力”培养的部分反馈信息为：有效的口头沟通能力（重要度为72%，满足度为86%）；积极思考及解决问题能力（重要度为72%，满足度为84%）；科学分析能力（重要度为65%，满足度为86%）；说服他人（重要度70%，满足度为78%）的能力，等．

表1 不同国家对“关键能力”的不同内涵定义

根据对口中、高职教育专家对关键能力内涵的理解和分析，同时归纳总结第三方调查公司给出的关键能力要素，结合区域经济特征及行业企业反馈，结合珠三角中、高职学生的实际情况，及考虑指标框架的简明性及可操作性，得出关键能力评价指标见表2．

2.2 构建比较判断矩阵

构建判断矩阵是层次分析法的关建之一．其过程实际上是对同一层次上的因素进行优先顺序的两两比较．根据层次分析法（AHP）的计算步骤，结合成对比较标度含义表（表3），对各相关指标分别进行两两比较评分．首先将第一级中的4项指标（一级指标）两两比较，例如：学习能力Q1重要程度稍强于社会能力Q2，其数值就为“3”，反过来则为“1/3”，如果同样重要，其数值就为“1”，同理类推．在建立判断矩阵时，由校内专家、行业企业人员、在校学生、毕业学生等多层面的人员共同参与数据采集，保证了数据来源的可靠性．为简化数据分析过程，以专家团队形成的一级指标判断矩阵见表4，二级指标判断矩阵同理可得，见表5．

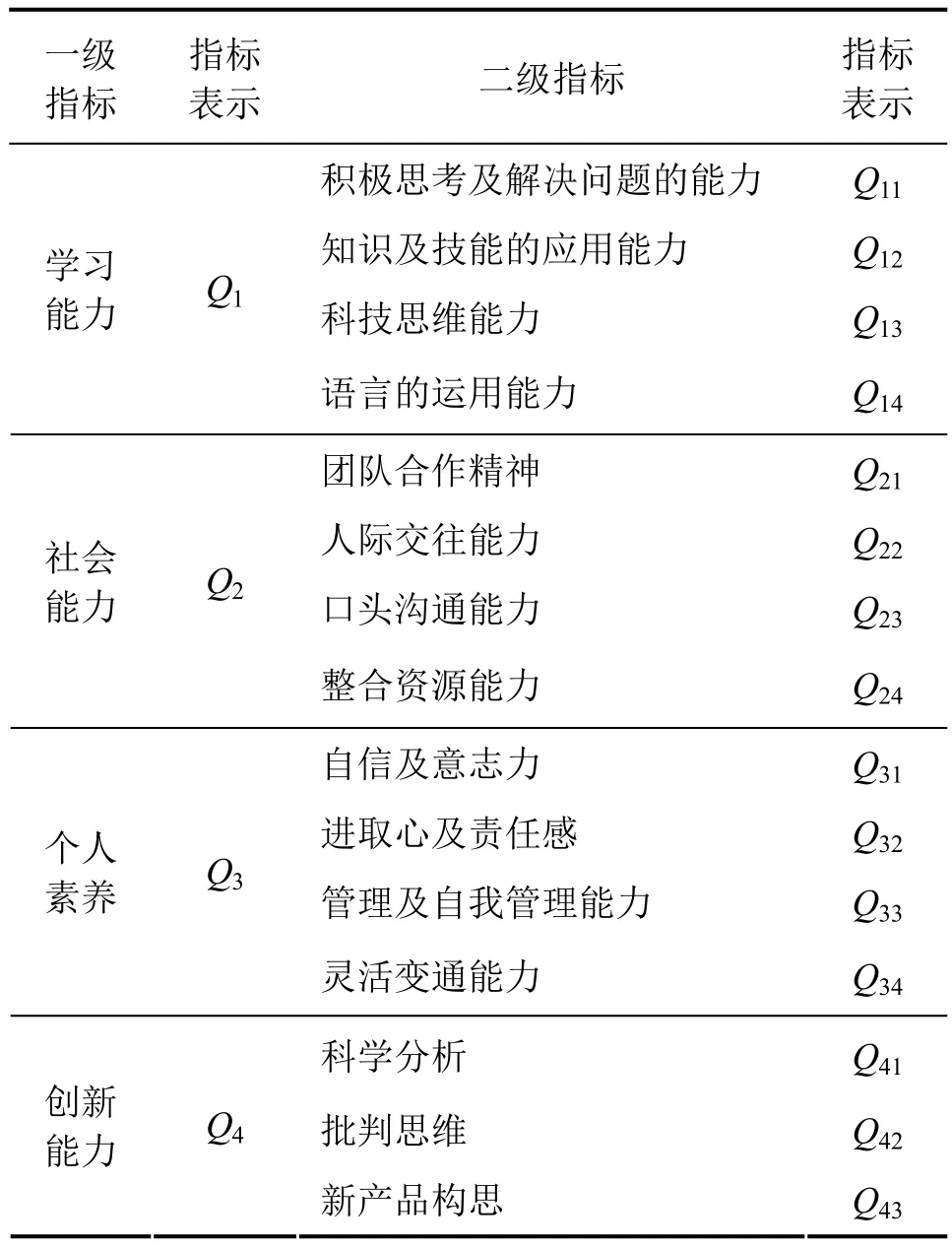
表2 中高职学生关键能力评价指标表

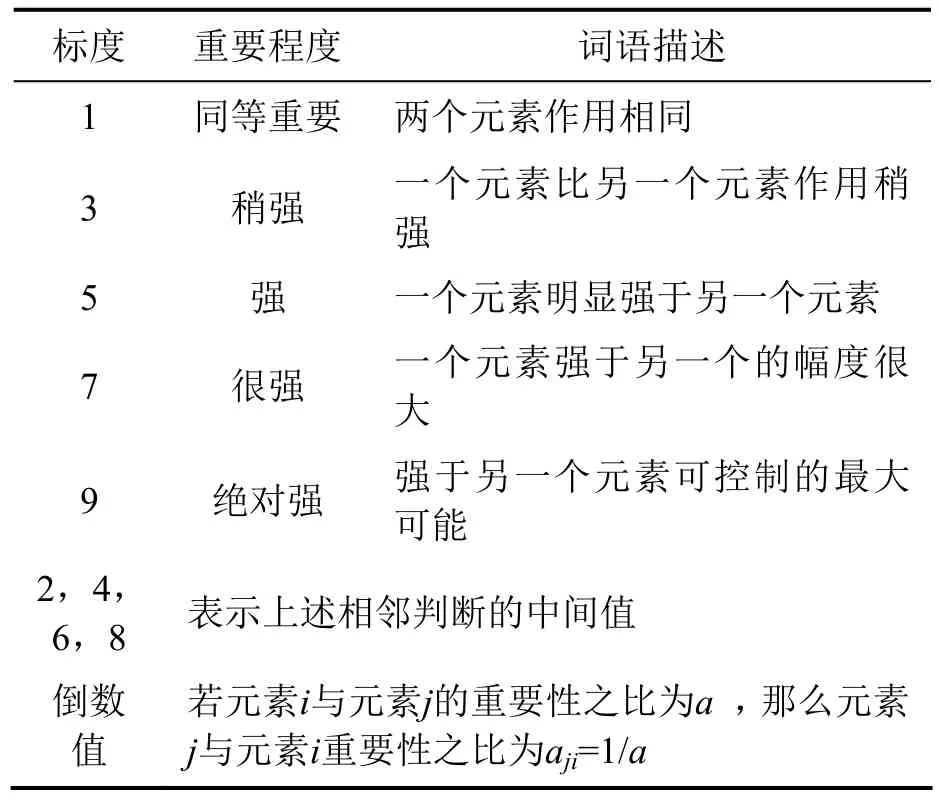
表3 1-9比例标度的含义

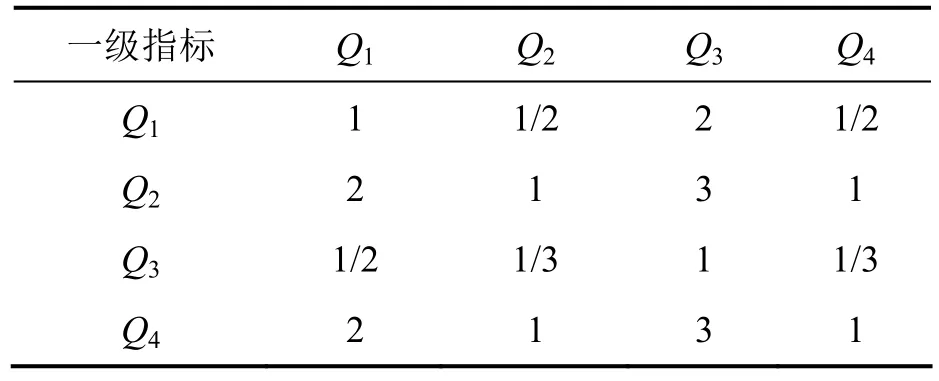
表4 专家一级指标判断矩阵

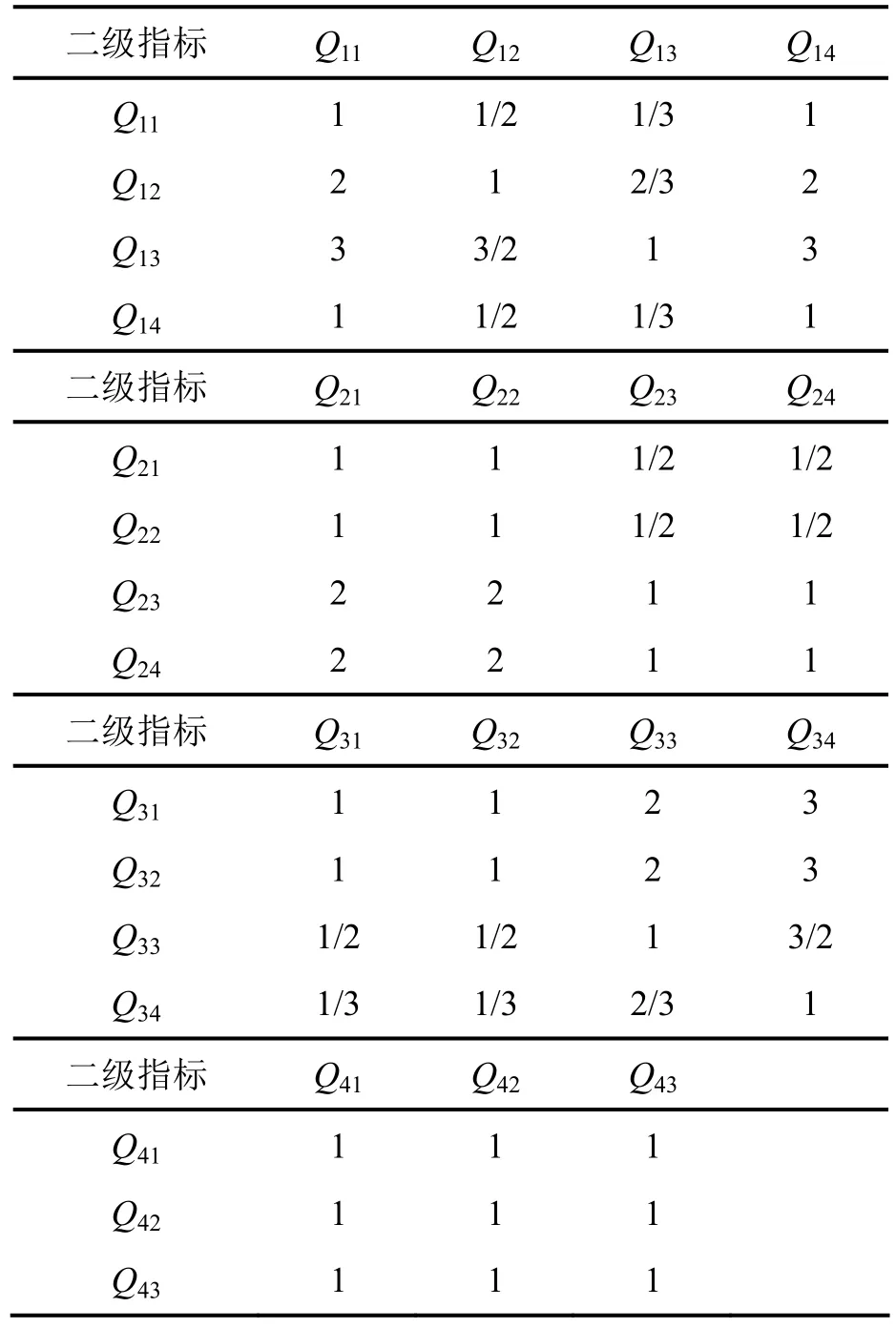
表5 专家二级指标判断矩阵

2.3 判断矩阵的一致性检验

按以上方法所采集的矩阵数据，如满足一致性检验要求则数据可用，否则需丢弃该数据或与被调查者沟通，对矩阵进行调整．一致性指标CI=(λmax-n)/(n-1), λmax为判断矩阵的最大特征值，n为判断矩阵阶数．一致性比率CR=CI/RI，RI为同阶矩阵随机指标．如CR>0.1则一致性差，需重估；如CR<0.1，则矩阵满足一致性要求．因此，可求得与矩阵阶数n相应的临界特征值λ′max=CI*(n-1)+n=CR*RI*(n-1)+n=0.1*RI*(n-1)+n ．当λmax<=λ′max时，则通过一致性检验．按此原理用MATLAB软件检验专家一级指标判断矩阵，得λmax=4.01<λ′max=4.27，通过一致性检验．同理可验其他采集矩阵群的一致性，保证最终进行计算的所有矩阵均通过一致性检验．

2.4 规范列平均法（和法）计算权值

利用相同的计算方法，分别求出一级指标和二级指标的权值．一级指标权值规范列平均法的具体计算步骤为：

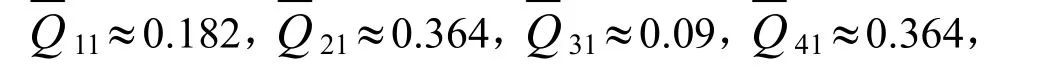
同理可得：

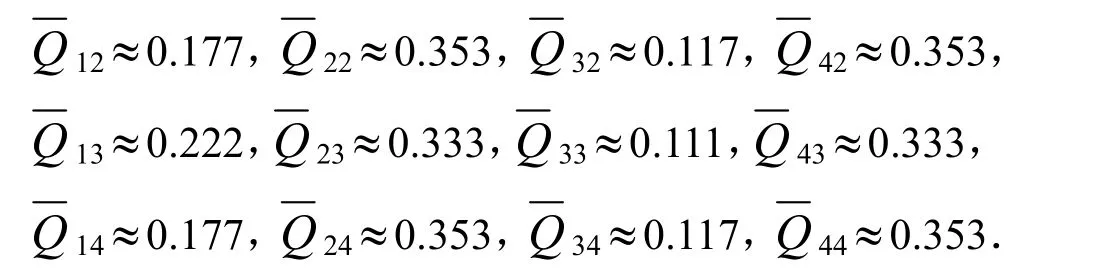
W1=1/4(0.182+0.177+0.222+0.177)=0.1895；

W2=1/4(0.364+0.353+0.333+0.353)=0.3508；

W3=1/4(0.09+0.117+0.111+0.117)=0.1088；

W4=1/4(0.364+0.353+0.333+0.353)=0.3508．

由此可见，对中高职学生关键能力的培养，笔者所在的珠三角地区，专家较为关注的为学生的社会能力及创新能力培养．这与珠三角地区高职毕业学生的职业转换率及自主创业情况是高度相关的．据此，在制定中高职衔接一体化培养方案时，应加强对学生社会能力及创新能力的一贯性培养，结合二级指标权重，有效分布相应的能力提升课程，从而达到与区域经济的用人需求一致性对接的目的．

3 结束语

关键能力是一个比较广泛的概念，涉及的指标项目也比较繁多．在中高职衔接培养过程中，其指标的设立，应针对不同的区域、结合不同的行业企业和学校自身定位有不同的一级、二级指标设计与划分，其得出的权重值也因此会有所不同．无论指标如何设定，“结合区域经济特征构建中高职学生关键能力评价调查表→采集多方位数据作为样本数据→通过层次分析法得出分析结果”，这种分析模式均可以采纳．通过这种模式对关键能力数据信息的分析，可以提供给相应的中、高职学生在一贯制学习中能力发展方向的数据建议，通过获取到的挖掘知识，可以有效地制定或改进学生关键能力培养策略，进一步提高学生的就业竞争力．

数据挖掘技术中的层次分析法把定性和定量方法结合在一起，能够处理许多用传统的最优化技术无法着手的实际问题，同时可增加决策的有效性，因此，为研究其他学生能力的类似问题提供了一种可行的解决方法．同时，在使用AHP方法时应注意到，在建立层次结构模型，及构造判断矩阵的过程中，较多依赖人为主观选择作为构造及判断的依据，这在样本数量不够或者信度不够的情况下会严重影响结果．解决的办法一是采集各层次群体数据，扩大数据采样范围；二是引入专家系统，提高判断的可信度．

[1] 王丹．数据挖掘在高职院校教学管理中的应用[J]．清远职业技术学院学报，2010，12：106-108．

[2] 岳延红．大学生英语素质教育评价研究[J]．科技信息，2012（4）：53-54．