基于子航迹Hough变换的模糊航迹关联

范 恩，谢维信，刘宗香

1)西安电子科技大学电子工程学院，西安710071;2)深圳大学ATR国防科技重点实验室，深圳518060

信息融合是研究和处理信息理论问题的方法之一［1-2］.多传感器多目标跟踪是利用来自多个传感器的信息，获取更精确、更完整的估计和决策［1-4］.航迹关联是多目标跟踪的前提，其算法设计与系统的融合结构以及传感器的类型紧密相关.与集中式融合结构相比，分布式融合结构能够以较低的费用获得较高的可靠性和可用性，对节点的数据处理能力和通信带宽要求较低，系统的可扩展性较好，在实际中被广泛应用.根据数据传输的路径，分布式融合结构分为完全分布式和多级分层式两种融合结构［4］.根据是否利用全局状态估计，航迹关联分为传感器航迹-传感器航迹关联和传感器航迹-系统航迹关联.在大规模分布式传感器网络中，由于传感器分布广、数目多，每个节点需要处理大量数据，且节点的数据处理能力和通信能力均是有限的，因此系统对航迹关联的实时处理能力提出了更高的要求.

航迹关联的核心是如何快速地判断来自不同传感器平台的航迹是否代表同一个目标，主要分为两类:基于统计的方法［5］和基于模糊的方法［6］.近年来，统计航迹关联主要考虑到与实际噪声、偏差、高维状态信息以及属性信息等有关的航迹关联问题［5-8］.由于实际噪声、各种误差彼此相关，以及关联判决中存在较大的不确定性，使得统计航迹关联的计算过程变得十分复杂.模糊航迹关联凭借模糊数学对不确定性问题的强大处理能力，具有较快的处理速度，较低的存储量与通信量，适用于存在较大误差的系统［3］.传统的模糊航迹关联算法进行单次关联判决时，只能够处理一对局部状态估计，为了满足关联质量，至少需要进行多次关联处理才能更新系统航迹，这样不仅约束了系统航迹的更新时间，而且难以用于多局部节点的情况［9］.文献［8］将待关联的航迹映射为高维空间中一组点集，利用加权模糊聚类很好地解决多局部节点的航迹关联问题，但是由于待关联对象是整条航迹，增加了系统航迹的更新时间，难以满足系统的实时处理要求.如果将航迹关联分解为局部状态估计-航迹关联，那么其可看作是类似于量测-航迹关联.文献［10］提出一种两点式数据关联算法，利用传感器连续两次扫描所获得的回波计算与目标的关联概率，通过增加单次关联对象的信息量来提高关联精度，为航迹关联提供一种思路.此外，在信息理论中，通过各种变换研究信号在不同空间的性质以及处理方法，也为航迹关联提供一种理论依据［8，11］.

在实际多级分层融合系统中，传感器航迹(或称局部航迹)数据是以报文依次从局部节点(或称传感器节点)发送到融合中心.本研究根据实际数据传输方式，将融合中心相邻时刻的同源局部状态估计定义为子航迹，提出一种基于子航迹Hough变换的模糊航迹关联方法(fuzzy track association using tracklet-based Hough transform，THT-FTA).该方法通过Hough变换将同一时间段的子航迹映射为参数空间中一组点集，再利用最大熵模糊聚类实现子航迹-系统航迹关联，最后通过仿真实验和实测实验分别对提出方法的有效性和可行性进行验证.

1 子航迹定义与映射

1.1 子航迹定义

如图1所示，在多级分层融合系统中，有1个融合中心F0和n个局部节点Ss，s=1，2，…，n.在实际系统中，每个局部节点需要建立两类航迹:用于本节点跟踪的传感器航迹，以及用于向融合中心上报的子航迹［12］.每条子航迹都是通过批估计法或序贯滤波法，由同一传感器在各报知时间内所采集的量测生成;利用子航迹能够避免上报冗余信息，降低系统对通信能力的要求［10］.

图1 多级分层融合模型Fig.1 Hierarchical fusion model

为了节约通信带宽，传感器航迹的局部状态估计一般是以报文依次从局部节点发送到融合中心，在融合中心生成系统航迹.为此，分别定义子航迹和候选子航迹为

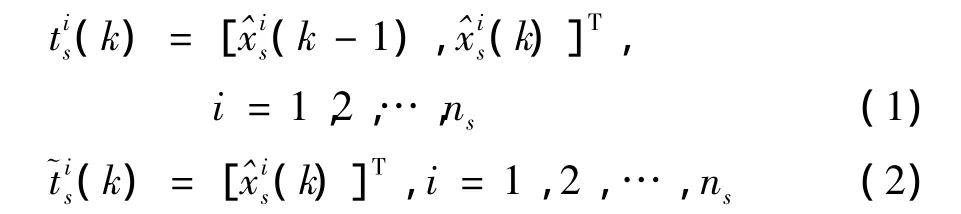
子航迹与候选子航迹的形成过程如图2.当融合中心F0收到传感器Ss发送的局部状态估计is(k)时，判断候选子航迹序列中是否存在同源候选子航迹.若存在，则生成子航迹tis(k);若不存在，则生成候选子航迹~is(k).

1.2 子航迹映射

图2 子航迹-系统航迹关联Fig.2 Tracklet-system track association

由于子航迹包含多个序贯的局部状态估计，相对单个局部状态估计，可以提供更多的关联信息，从而降低关联的不确定性，为此本研究将传感器航迹-系统航迹关联分解为子航迹-系统航迹关联.通常，传感器航迹持续的时间较长，是非线性的;子航迹持续的时间较短，局部状态估计的相对变化率较小，可以近似看作是线性的.因此，在同一时段的子航迹可以看作同一平面内的直线序列.在数据传输过程中，一般仅在起始阶段或目标高度变化时才上报高度信息，下面主要讨论目标高度变化小于给定阈值的情况.若将子航迹映射为参数空间的点，则子航迹-系统航迹关联可进一步转化为点的分布问题;利用点分布的几何特征与聚类分析，为研究航迹关联提供一种新思路.根据Hough变换

其中，f(·)为子航迹 tis(k)到点psi的映射函数;(ρsi，θsi)为点 psi的坐标，

相应地，子航迹序列可以映射为点集

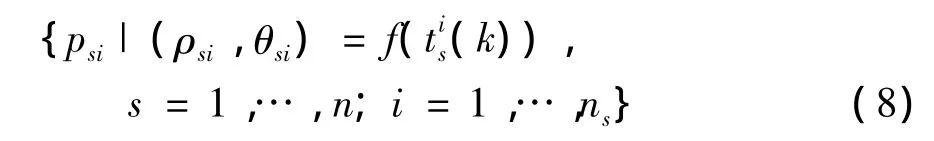
若存在多条子航迹源于同一目标，则这些子航迹对应的点会聚集.因此可通过Hough变换将子航迹-系统航迹关联转化为参数空间中点的聚类分析.为了更好地实现聚类，需要对ρ和θ进行归一化处理

ρ'=ρ/ρmax，θ'=θ/θmax

其中，ρmax和θmax分别为ρ和θ的最大值，与目标的空间分布及运动情况有关.

2 基于子航迹Hough变换的模糊航迹关联

最大熵模糊聚类［13］能够获得隶属度的最小无偏估计，具有聚类效果好、数学含义明确和物理意义清晰的优点.由于源于同一目标的子航迹之间具有较大的关联概率，聚类效果受目标空间分布的影响较小，因此本研究采用最大熵模糊聚类用于子航迹-系统航迹关联.

2.1 航迹关联中的最大熵模糊聚类

设在k时刻，传感器 Ss有ns条传感器航迹{ti，融合中心F有c条系统航迹{ti}，同时s00生成nk条子航迹{tis(k)}.通过Hough变换，计算出子航迹在参数空间的点集P={pi.给定vi为第 i类的聚类中心，V=［v1，v2，…，vc］T;uli=u1(pi)为点pi对聚类中心vi的隶属度，U={uli}为c×nk阶实矩阵.将子航迹-系统航迹关联转化为参数空间中点的聚类分析，具体的聚类过程可以描述为一个优化过程.首先构造代价函数

其中，d(pi，vl)= pi-vl2为点pi到聚类中心vl的欧式距离;uli服从如下约束

再根据Shannon定理可得

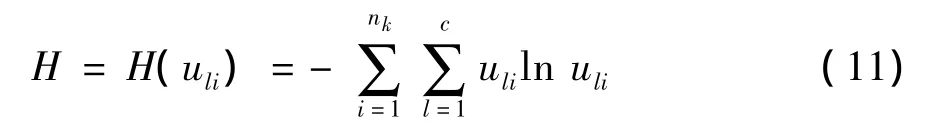
在式(9)和式(10)的约束下，最大化式(11)，并利用Lagrange乘子法构造目标函数

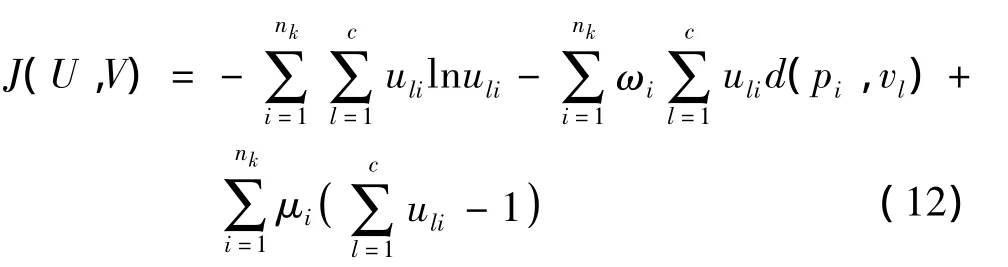
其中，ωi和μi为拉格朗日乘子.从而解得

这里，ωi称为差异因子.通过控制ωi，可以调整隶属度uli的大小.为了减少迭代次数，将系统航迹的当前与下一时刻的预测值映射为参数空间中的聚类中心，即vi=f(［i0(k-1)，i0(k|k-1)］T).对应的预测方程为

其中，H(k-1)和F(k-1)分别为(k-1)时刻的观测转移矩阵和状态转移矩阵.THT-FTA方法流程图如图3.

图3 THT-FTA方法的流程图Fig.3 Flow chart of THT-FTA method

2.2 差异因子分析

由文献［13］知，ωi的取值与具体应用有关，其最优值的一般形式为

其中，dlmin=min{d(pi，vl)}ci=1;ε为一正常数.在聚类过程中，点到聚类中心的距离越近，对应的子航迹与系统航迹的关联概率越大.另外，传感器的虚警率越低，源于该传感器的子航迹的关联可信度越高.因此，在航迹关联中ωi可定义为

其中，ξi为对应传感器的虚警率，η为一正常数.当目标密集、传感器较多时，可以选择合适的隶属度阈值，然后确定距离门限:如果点与聚类中心的距离大于距离门限，可以忽略该点的隶属度，从而进一步减小聚类算法的计算量.

3 结果及分析

为验证算法的有效可行，分别以仿真、实测实验为例，将THT-FTA方法与加权模糊聚类的航迹关联算法(track association using weighted fuzzy clustering，wFC-TA)［9］及模糊航迹关联算法(fuzzy track association，FTA，关联质量 m=6)［3］进行比较.实验平台参数为:Pentium(R)，CPU双核2.93 GHz，内存 1 Gbit，运行环境 Matlab r2009b.

3.1 仿真实验

设空中有4批交叉运动的目标，均做匀速直线飞行，飞行高度保持1.0 km，目标的初始状态分别为(9.0 km，200 m/s，7.4 km，200 m/s)T、(9.0 km，200 m/s，7.3 km，200 m/s)T、(9.0 km，200 m/s，7.2 km，200 m/s)T和(9.0 km，200 m/s，6.2 km，200 m/s)T.在分布式融合系统中，有1个融合中心和4部雷达，站址分别为(15 km，24 km)、(8.5 km，4.5 km)、(21 km，4.5 km)、(8.5 km，24 km)和(21 km，24 km);雷达性能参数为:测距误差 σr=100 m，测角误差 σθ=0.1°，采样周期T=3 s，各雷达同步采样，观测结果如图4.系统的数据处理过程为:各雷达先将采集的数据生成雷达航迹，再将局部状态估计从雷达坐标系变换到全局直角坐标系，然后逐个发送到融合中心，同时生成子航迹，最后采用提出方法实现子航迹-系统航迹关联，并利用加权平均航迹融合算法(weighted average track fusion，wATF)［14］进行融合.

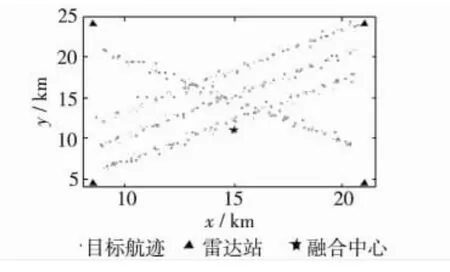
图4 含噪声的雷达航迹Fig.4 Radar tracks with noises

图5给出第2个周期内，子航迹经过Hough变换后，参数空间中点的分布情况.图6是通过THT-FTA进行关联，再采用wATF得到的系统航迹.一般地，在传感器测量空间，聚类算法的性能与目标的数量及分布有关［15］.由图5可见，在同一周期内，由于源自同一目标的子航迹具有较大的关联概率，经过Hough变换后，对应参数空间的点具有明显可分性，从而验证通过参数空间中聚类实现子航迹-系统航迹关联是可行的.

图5 参数空间中模糊聚类Fig.5 Fuzzy clustering in parameter space

图6 系统航迹的融合结果Fig.6 Fusion results of system tracks

由图6可见，利用wATF可以获得精确的融合结果，间接地证明通过THT-FTA能准确实现子航迹关联.对3种算法分别运行100次Monte Carlo仿真，表1给出了它们的系统航迹平均更新时间和多局部节点处理能力.由表1可见，THT-FTA做关联判决时，关联对象为子航迹，一次能够处理同一时刻内所有的子航迹，且通过将预测中心作为聚类的初始值可以进一步减少迭代次数，因此不仅能够满足多局部要求，而且系统航迹平均更新时间最少;wFC-TA做关联判决时，一次能够处理同一周期内所有的雷达航迹，关联对象为整条航迹，因此也能够满足多局部节点要求，但系统航迹平均更新时间比THT-FTA多;FTA做关联判决时，关联对象为局部状态估计，一次仅能处理一对局部状态估计，且为了满足关联质量m，至少需要m次关联处理才能更新系统航迹，因此不仅难以满足多局部节点处理要求，且系统航迹平均更新时间最长.

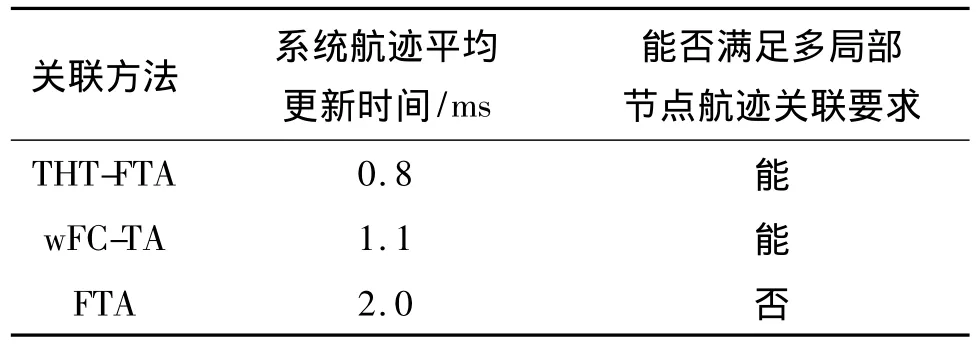
表1 算法性能比较Table1 Comparison of the algorithms'performances

3.2 实测实验

采用Ⅰ和Ⅱ两部同型号雷达跟踪空中6批目标，如图7.雷达及融合中心站址分别为(117.815 11°，33.537 26°，0 m)、(120.999 49°，30.842 36°，0 m)和(119.407 30°，32.189 81°，0 m);雷达性能参数为:最大探测距离rmax=230 km，测距误差σr=100 m，测角误差σθ=0.5°，扫描周期 T=3 s.表2给出各雷达实测航迹的起始位置，高度均为1.0 km.具体数据处理过程为:在雷达节点，将雷达航迹数据从局部坐标系变换到地理坐标系，并进行时间对正，然后发送至融合中心;在融合中心，将雷达航迹数据从地里坐标系，经地心坐标系，变换到全局坐标系，并生成子航迹;最后采用本文方法对子航迹-系统航迹进行关联，并利用wATF进行融合.图7给出地理坐标系中各雷达的实测航迹.图8给出采用THT-FTA和wATF在全局直角坐标系的处理结果，从而间接验证了提出本文方法的可行性.

表2 实测航迹的起始位置Table2 Initial positions of real tracks

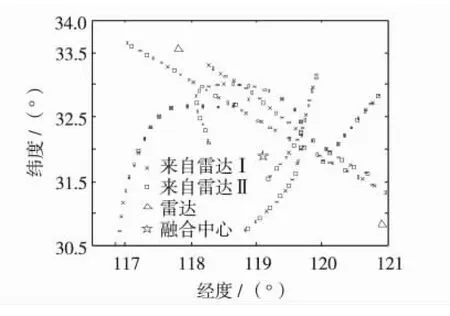
图7 实测航迹Fig.7 Real tracks

图8 融合结果Fig.8 Fusion results

结 语

针对分布式融合系统中多局部节点的航迹关联问题，提出一种基于子航迹Hough变换的模糊航迹关联方法.该方法根据实际系统中数据的传输方式，定义融合中心相邻时刻的同源局部状态估计为子航迹，通过Hough变换将同一时段的所有子航迹映射为参数空间中一组点集，从而将航迹关联转化为参数空间的聚类分析.在关联过程中，采用子航迹与系统航迹关联，能够减少系统航迹的平均更新时间，更好地满足系统的实时处理要求;通过参数空间中模糊聚类能够实现航迹关联的并行处理，分类精度也随着关联对象的信息量的增加而提高.实验结果证明，针对多局部节点情况，提出算法能够准确实现子航迹-系统航迹关联，与加权模糊聚类的航迹关联算法相比，具有较快的关联处理速度.

/References:

［1］Pek H F，Gee W N.High-level information fusion:an overview ［J］.Journal of Advances in Information Fusion，2013，8(1):1-40.

［2］Bahador K，Alaa K，Fakhreddine O K.Multisensor data fusion:A review of the state-of-art［J］.Information Fusion，2013，14(1):28-44.

［3］He You，Wang Guohong，Guan Xin，et al.Information fusion theory with applications［M］.Beijing:Publishing House of Electronics Industry，2010:239-241.(in Chinese)何 友，王国宏，关 欣，等.信息融合理论及应用［M］.北京:电子工业出版社，2010:239-248.

［4］Qiao Xiangdong，Li Tao.Survey of multi-sensor track fusion ［J］.Systems Engineering and Electronics，2009，31(2):245-250.(in Chinese)乔向东，李 涛.多传感器航迹融合综述 ［J］.系统工程与电子技术，2009，31(2):245-250.

［5］Osborne R W，Bar-Shalom Y，Willett P.Track-to-track association with augmented state［C］//Proceeding of International Conference on information fusion.Chicago(USA):IEEE Press，2011:1-8.

［6］Aziz A M.Fuzzy track-to-track association and track fusion approach in distributed multisensor-multitarget multiple-at tribute environment［J］.Signal Processing，2007，87(6):1474-1492.

［7］Jing Peiliang，Liu Fang.Track association method using modified fuzzy membership ［J］.Journal of Applied Sciences，2012，30(2):181-186.(in Chinese)井沛良，刘 方.一种使用修正模糊隶属度的航迹关联方法 ［J］.应用科学学报，2012，30(2):181-186.

［8］Gao Xinbo，Li Jie.A feature-weighted fuzzy clustering algorithm for track association in sensor network ［J］.Acta Electronic Sinica，2007，35(12):148-151.(in Chinese)高新波，李 洁.传感器网络中航迹关联的加权模糊聚类算法 ［J］.电子学报，2007，35(12):148-151.

［9］Fan En，Xie Weixin，Liu Zongxiang，et al.A novel fuzzy track association algorithm in distributed sensor network［J］.Signal Processing，2011，27(10):1561-1565.(in Chinese)范 恩，谢维信，刘宗香，等.分布式传感器网络中一种新的模糊航迹关联算法 ［J］.信号处理，2011，27(10):1561-1565.

［10］Li Hui，Zhang An，Zhao Min，et al.Multiple maneuvering target tracking based on two-scan data association［J］.Acta Electronica Sinica，2005，33(12):2125-2129.(in Chinese)李 辉，张 安，赵 敏，等.基于两点式数据关联算法的多机动目标跟踪［J］.电子学报，2005，33(12):2125-2129.

［11］Tian Hongwei，Jing Zhongliang.A multi-space data association algorithm for target tracking systems［J］.Communications in Non-linear Science and Numerical Simulation，2007，12(4):608-617.

［12］Ge Qinge，Li Junling.Analysis of the Principle for the elimination of redundant information in distributed fusion［J］.Command Information System ＆ Technology，2010，1(6):12-15.(in Chinese)葛勤革，李君灵.分布式融合中冗余信息消除原理分析 ［J］.指挥信息系统与技术，2010，1(6):12-15.

［13］Li Liangqun，Ji Hongbing，Gao Xinbo.Maximum entropy fuzzy clustering with application to real-time target tracking［J］.Signal Processing，2006，86(11):3432-3447.

［14］Huang Youpeng，Zhou Yongfeng，Zhang Haibo，et al.Algorithm of weighting factors dynamic allocation in multi-radar track weighted fusion ［J］.Computer Applications，2008，28(9):2452-2454.(in Chinese)黄友澎，周永丰，张海波，等.一种多雷达航迹加权融合的权值动态分配算法 ［J］.计算机应用，2008，28(9):2452-2454.

［15］Hall D L，Llinas J.Handbook of Multisnesor Data Fusion［M］.Yang Lujin，Geng Boying，trans.Beijing:Publishing House of Electronics Industry，2008:50-53.(in Chinese)Hall D L，Llinas J.多传感器信息融合手册 ［M］.杨露菁，耿伯英，译.北京:电子工业出版社，2008:50-53.