超声辐射力弹性成像系统研究及仿体实验

陈 昕，郭燕荣，王 毅，沈圆圆，林浩铭，朱 颖，郑 翊，汪天富，陈思平

1)医学超声关键技术国家地方联合工程实验室，广东省生物医学信息检测与超声成像重点实验室，深圳大学医学院，深圳518060;2)美国圣克劳德州立大学电子与计算机工程系，圣克劳德56301，美国

生物组织弹性 (硬度)的变化可很好地表征病理学上的变化［1］，所以组织弹性信息的提取对临床诊断具有重要价值.临床上常用的影像诊断技术，如超声、X线、CT和MRI，主要针对人体组织和器官的解剖结构成像，无法提供组织弹性信息，对形态无变化，但硬度已远远有别于周围组织的病灶，如乳腺和前列腺肿瘤，无法诊断［2-3］.若能定量获得组织的弹性系数并对其成像，必将对肿瘤的早期诊断产生重要的推动作用.

目前对于组织弹性成像方法大多基于超声弹性成像［4］和磁共振(magnetic resonance，MR)弹性成像［5］.相比MR弹性成像费用昂贵，超声弹性成像更易于在临床推广.根据组织激励方式或检测方法的不同，超声弹性成像可分为准静态弹性成像［4，6］、低频振动弹性成像［7］、剪切波弹性成像(shear wave elasticity imaging，SWEI)［8］、声辐射力脉冲成像(acoustic radiation force impulse imaging，ARFI)［9］、快速剪切波成像 (supersonic shear imaging，SSI)［10］和振动声成像 (vibro-acoustography，VA)［11］等.目前的大多数方法都忽略了组织的黏性，一方面，这会造成弹性系数估计偏差;另则，组织的黏性系数也是表征病理学变化的重要参数.

剪切波频散超声振动成像 (shear wave dispersion ultrasound vibration，SDUV)通过测量不同振动频率下剪切波传播速度对组织黏弹性系数进行定量测量.这种方法在激励端可准确定位，使被激励部分高度局部化，在检测端对微小振动的检测和提取非常有效，是一种有应用前景的超声辐射力弹性成像方法，离体和在体实验均显示该方法对组织黏弹性系数测量结果较理想［12-13］.

本研究开发了用于超声辐射力弹性成像研究的通用实验系统，可进行ARFI或SDUV研究.采用SDUV的方法，完成初步的琼脂仿体和离体大鼠肝脏的黏弹性系数测量实验，验证剪切波频散超声振动成像的原理及整个系统的可操作性和实用性.

1 超声辐射力弹性成像系统研究

在各向同性的均匀介质中，剪切波的传播速度［14］可表示为

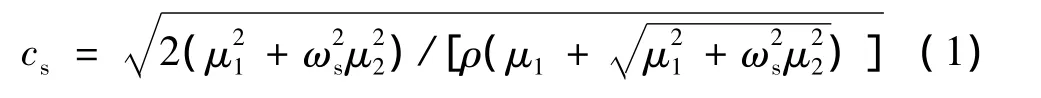
其中，cs为剪切波传播速度;ωs为角频率;ρ为介质密度;μ1和μ2为介质弹性与黏性系数.从式(1)可见，介质内一定频率剪切波传播速度由介质密度、弹性系数和黏性系数决定.另一方面，剪切波的速度可由传播过程中一定距离上的相位差估计得到

其中，Δφs为相距Δr的两点的相位差.可见，只要求得一定距离上剪切波的相位差，就可获得该频率剪切波的传播速度，若介质中有多个频率剪切波在传播，依次计算各频率的剪切波速度，代入式(1)，则可拟合得到介质的弹性系数与黏性系数.

要实现超声辐射力弹性成像系统，需激励组织产生振动并对振动进行检测，且需在此过程中实现自动控制和数据处理以得到组织黏弹性系数.本研究分别从硬件和软件部分对系统进行设计.硬件包括激励部分和检测部分，激励部分发射激励脉冲，聚焦于组织内某一区域，激励该区域振动并产生剪切波的传播;检测部分对剪切波传播路径上相隔距离Δr的一系列点进行检测，并实现回波采集.软件包括系统控制程序和数据处理程序，系统控制程序完成仪器的自动控制从而实现系统自动化;以卡尔曼滤波算法为主的数据处理程序则用于实现振动相位的估计和黏弹性系数的计算.

1.1 系统硬件组成

硬件系统包括激励与检测两个部分，如图1.激励部分由函数发生器2输出幅度调制的波形，经功率放大器放大后用于驱动激励探头.检测部分由脉冲收发机驱动单阵元检测探头发射检测脉冲，并对回波进行接收放大.数据采集卡将模拟回波采样为数字信号并保存.主机控制整个系统的运行以及进行数据处理，激励探头与检测探头分别固定在三轴位移台上并由位移台完成定位.

激励序列与检测序列的时序如图2.其中，激励脉冲重复频率fs=100 Hz;检测脉冲重复频率PRF=2 kHz.这两个序列在时域上是间隔的，检测序列相对激励序列存在延时，如此即可避免两序列间的相互干扰.函数发生器1作为主控触发，产生两路触发信号分别控制激励脉冲和检测脉冲，使整个系统的时序同步，保证在各点上获得的相位信息准确有效.系统采用的激励序列为100 Hz调幅波形，这种激励序列可同时产生100、200、300和400 Hz等频率的谐波，这样就无需为了得到不同频率剪切波的速度而不断改变激励序列的脉冲重复频率.

图1 超声辐射力弹性成像系统框图Fig.1 Diagram of ultrasonic radiation force elastography system

图2 激励序列与检测序列时序Fig.2 Timing of the excitation beam and detection beam

系统总体实物图如图3(a)，激励探头和检测探头分别固定于三轴位移台，并与水缸同置于光学防震台上，这样可有效降低外界振动对实验的影响.如图3(b)，仿体通过支架固定于水缸中，激励探头和检测探头聚焦于仿体内的某点.水缸的下表面黏附有吸声材料，可有效吸收穿过仿体到达水缸下表面的声波，避免因其反射影响检测结果.

1.2 系统软件程序设计

本研究开发了相应的控制和数据处理程序，实现了系统采集与控制的自动化及数据后处理.

系统内所有仪器通过总线与计算机相连.采用LabView进行系统控制程序的开发.数据处理程序用Matlab软件编写，实现从回波信号中估计各频率剪切波的振动相位，从而计算仿体黏弹性系数.

图3 系统实物图Fig.3 Photos of the system

Zheng等［13］对如何从连续回波信号中提取振动相位给出了详细的推导.使用脉冲周期为T的检测脉冲对振动进行检测时，第k个回波可表示为

其中，β =2Dω0cos θ/c，D为振动幅度;ω0为检测探头中心频率;θ为检测探头和激励探头之间的夹角;c为超声声速;φ0是相位常数;g(t，k)是 r(t，k)的复包络;ωs为剪切波振动频率;φs为振动相位.由式(3)可见，组织振动信息 βsin［ωs(t+kT)+ φs］被包含在了超声回波中.利用相邻回波之间的相位差别可提取振动，而此相位差别可通过分析复速度量得到，复速度量可定义为

其中，X为复速度量的实部;Y为复速度量的虚部;g(t，k)和g*(t，k+1)为相邻的第k个和k+1的回波的复包络;*表示共轭运算.因此，振动速度为

这里，s(t，k)表征的是组织在某一位置处的振动，其幅度和相位随距离振动点位置的改变而改变.通过比较 s(t，k)在不同位置z和z+Δz的相位φs，可得到相应的相位差

由于激励组织产生的振动较微弱，所以易受噪声干扰.若使用正交解调或者中心频率为振动频率的带通滤波器提取相位则很容易使估计产生偏差.本研究采用卡尔曼滤波技术对振动相位进行估计，这是因为卡尔曼滤波是以最小均方误差为准则的递推最优估计理论，适用于对频率已知、幅度和相位随机的信号估计［15］.

2 仿体黏弹性系数测量实验

为验证基于超声辐射力弹性成像系统的有效性，本研究采用完成琼脂仿体和离体大鼠肝脏仿体黏弹性系数测量实验.

2.1 琼脂仿体黏弹性系数测量实验

琼脂仿体使用HKM公司的050010琼脂粉制作，琼脂粉与水的质量比为1∶60，尺寸为10 cm×10 cm×10 cm，图4为琼脂仿体的实物图.为增大仿体受超声激励后振动的幅度，在制作仿体时，仿体上表面以下3 mm处嵌入一个直径为1 mm的焊锡珠，实验时使激励探头聚焦于焊锡珠进行激励.

图4 琼脂仿体Fig.4 Agar phantom

激励探头的中心频率为1.04 MHz，焦距为9 cm;检测探头的中心频率为5 MHz，焦距为4 cm.激励脉冲与检测脉冲的时序如图2.激励波形为100 Hz幅度调制波形，每个激励周期内含1.04 MHz的正弦波200 μs，激励10个周期，检测脉冲的脉冲重复频率为2 kHz.检测回波的采样频率为100 MHz.如图3(b)，琼脂仿体固定于支架内，并与支架一起浸入底部黏附有吸声材料的水缸.

实验时，首先将激励探头和检测探头共聚焦于琼脂仿体内部的焊锡珠上，然后检测探头向外移动1 mm，从距离振动源点1 mm处开始检测并估计相位差.图5为检测探头接收到的回波波形.

图5 检测回波波形Fig.5 Waveform of the ultrasound echo

检测剪切波传播路径上水平距离间隔为0.1 mm的3个点，并估计100～300 Hz的相位.由卡尔曼滤波估计这3个点的相位变化如图6.图6中的直线是对各频率相位估计值的回归分析，从中可计算各频率剪切波的声速.重复此实验3次，根据式(1)拟合得到该琼脂粉与水的质量比为1∶60的琼脂仿体的弹性系数与黏性系数统计均值为 μ1=(1.96 ±0.06)kPa，μ2=(0.55 ±0.12)Pa·s.

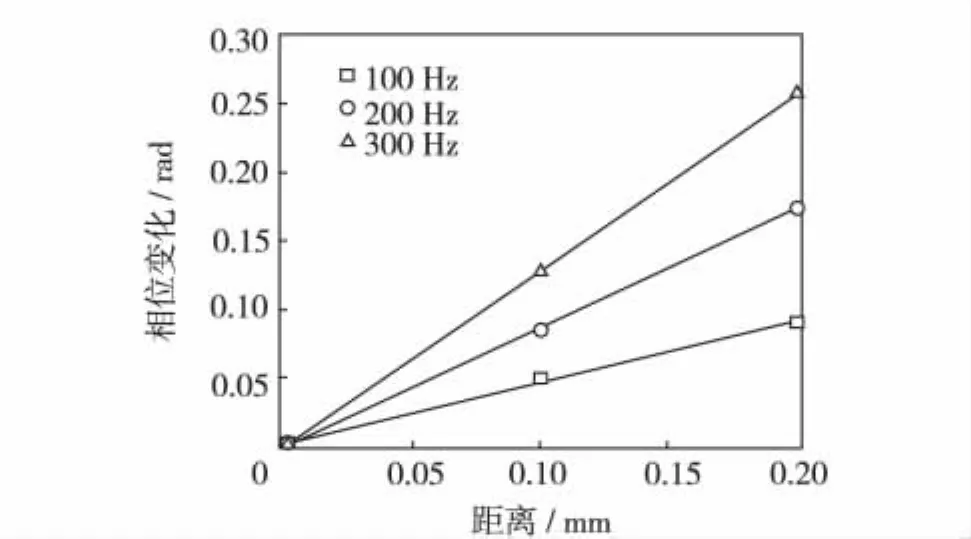
图6 卡尔曼滤波估计的3点相位变化Fig.6 Shear wave phase changes estimated by Kalman filter

Chen等［16］在类似材质和特性的琼脂仿体上测得μ1=(2.22±0.08)kPa，μ2=(0.32±0.03)Pa·s，本研究的测量结果与这些结果相近.

为更直观的进行比较和验证，本研究用相同的琼脂粉制作了另一块琼脂粉与水的质量比为1∶30的仿体，并采用相同参数和设置测定此仿体的黏弹性系数.

实验时，从距离激励点水平位置1 mm开始，检测剪切波传播路径上水平距离间隔为0.5 mm的5个点，并估计它们在100～400 Hz的相位.由卡尔曼滤波估计得到这5个点的相位变化，如图7.

图7 卡尔曼滤波估计的5点相位变化Fig.7 Shear wave phase changes estimated by Kalman filter

实验重复3次，拟合得到该1∶30琼脂仿体弹性系数统计均值μ1=(3.43±0.18)kPa，黏性系数 μ2=(0.42 ±0.15)Pa·s.与质量比为 1∶60 的琼脂仿体相比，质量比为1∶30的仿体的弹性系数增大，黏性系数减小，反映仿体制作时琼脂粉与水比例的差别.对由不同比例琼脂粉与水制成的仿体的测量结果显示，本系统对介质弹性系数与黏性系数的定量测量有区分度.

2.2 离体大鼠肝脏黏弹性系数测量实验

本研究还进行了离体的动物实验，完成对离体大鼠肝脏的黏弹性系数测定.大鼠是肿瘤实验研究中最常用的实验动物，它易患肝纤维化、肝癌，可用药物控制复制成各种肿瘤模型，且大鼠肝脏的内部相对较均匀，血管较小，在测量时易获得良好的原始数据.

图8 大鼠肝脏仿体Fig.8 Rat liver embedded in phantom

这批大鼠由广州动物实验中心提供，本研究对其进行生理解剖取出肝脏并制成仿体，为防止肝脏组织特性发生改变，仿体制作完的当天即进行实验.如图8，肝脏埋于凝胶仿体内.凝胶仿体使用SIGMA公司的G2500猪皮凝胶粉制作而成，这种凝胶粉制成的仿体与生物组织的性质比较接近，凝胶以质量分数为13%配制，仿体尺寸为10 cm×10 cm×5 cm.大鼠肝脏位于仿体的上半部分，厚约7 mm，肝脏上表面与凝胶仿体上表面持平.

实验参数设置与琼脂仿体实验相同.首先将激励探头和检测探头共同聚焦于大鼠肝脏下表面的同一位置，然后将检测探头水平外移1 mm，从距离振动源1 mm处每间隔0.5 mm依次测量5个点，并估计这5个点在100～400 Hz频率的相位.图9为由卡尔曼滤波估计这5个点的相位变化.

图9 卡尔曼滤波估计的5点相位变化Fig.9 Shear wave phase changes estimated by Kalman filter

实验重复3次，拟合得到该大鼠肝脏的弹性系数 μ1=(2.18±0.17)kPa，黏性系数 μ2=(0.61±0.07)Pa·s.

目前黏弹性系数测量的离体动物实验主要集中在对猪肝脏和大鼠肝脏黏弹性的测量.Salameh等［17］利用磁共振弹性成像的方法，测得大鼠肝脏的弹性系数μ1=(1.76±0.37)kPa，黏性系数μ2=(0.51 ±0.04)Pa·s.Nightingale 等［18］利用声辐射力脉冲成像的方法测量了大鼠肝脏，ARFI方法测得弹性系数μ1=(1.5±0.1)kPa.本研究的黏弹性测量结果与这些结果相近.

结 语

本研究设计并实现了超声辐射力弹性成像研究系统.基于该系统进行了初步的仿体实验:不同水含量的琼脂仿体的黏弹性系数测量结果具有合理差别，说明系统对不同介质黏弹性系数具有区分度，验证了剪切波频散超声振动成像的原理和方法;大鼠肝脏的黏弹性系数测量结果与其他结果相近，证明采用该系统进行离体动物实验可行.后续研究可对肝纤维化不同分期的大鼠肝脏进行黏弹性系数测量.若能实现对肝纤维化不同分期的定标，则对临床肝纤维化的早期发现及不同分期的定性具有重要参考价值.由于组织振动产生的剪切波信号很弱，且衰减快，如何准确检测组织的振动就很关键.下一步，本课题组将考虑使用Sonix-RP(Ultrasonix公司生产的开放式超声系统平台)进行剪切波检测，增强检测灵敏度和回波质量;同时考虑在检测中引入编码的方法，增强获取振动信号的信噪比［19-20］.

/References:

［1］ Fung Y C.Biomechanics:Mechanical Properties of Living Tissue［M］.New York:Spring-Verlag，1993.

［2］ Garra B，Cespedes I，Ophir J，et al.Elastography of breast lesions:initial clinical results［J］.Radiology，1997，202:79-86.

［3］ Wang Weiqi，Liu Bin，Wang Yuanyuan.Detection of human tissue elasticity using ultrasound and its application prospect［J］.Acoustic Technique，1998，17(3):98-102.(in Chinese)王威琪，刘 斌，汪源源.人体组织弹性的超声检测和应用前景 ［J］.声学技术，1998，17(3):98-102.

［4］ Ophir J，Cespedes I，Ponnekanti H，et al.Elastography:a quantitative method for imaging the elasticity of biological tissues ［J］.Ultrasonic Imaging，1991，13(2):111-134.

［5］ Muthupillai R，Lomas D J，Rossman P J，et al.Magnetic resonance elastography by direct visualization of propagating acoustic strain waves ［J］.Science，1995，269(5232):1854-1857.

［6］ Lubinski M A，Emelianov S Y，O'Donnell M.Speckle tracking methods for ultrasonic elasticity imaging using short time correlation［J］.IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control，1999，46:82-96.

［7］ Hoyt K，Castaneda B，Parker K.Two-dimensional sonoelatographic shear velocity imaging［J］.Ultrasound in Medicine and Biology，2008，34(2):276-288.

［8］ Sarvazyan A，Rudenko O V，Swanson S D，et al.Shear wave elasticity imaging:a new ultrasonic technology of medical diagnostics［J］.Ultrasound in Medicine and Biology，1998，24:1419-1435.

［9］ Nightingale K.Acoustic radiation force impulse(ARFI)imaging:a review ［J］.Current Medical Imaging Reviews，2011，7(4):328-339.

［10］ Tanter M，Bercoff J，Athanasiou A，et al.Quantitative assessment of breast lesion viscoelasticity:initial clinical results using supersonic shear imaging［J］.Ultrasound in Medicine and Biology，2008，34(9):1373-1386.

［11］ Fatemi M，Greenleaf J F.Ultrasound-stimulated vibro-acoustic spectrography［J］.Science，1998，280(5360):82-85.

［12］ Chen S G，Urban M，Pislaru C，et al.Shear wave dispersion ultrasound vibrometry(SDUV)for measuring tissue elasticity and viscosity［J］.IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control，2009，56(1):55-62.

［13］ Zheng Y，Chen S G，Tan W，et al.Detection of tissue harmonic motion induced by ultrasonic radiation force using pulse-echo ultrasound kalman filter［J］.IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control，2007，54(2):290-300.

［14］ Oestreicher H L.Field and impedance of an oscillating sphere in a viscoelastic medium with an application to biophysics［J］.The Journal of the Acoustical Society of A-merica.1951，23(6):707-714.

［15］ Brown R，Hwang P.Introduction to Random Signals and Applied Kalman Filtering［M］.New York:John Wiley＆ Sons Ltd，1997.

［16］ Chen S G，Fatemi M，Greenleaf J.Quantifying elasticity and viscosity from measurement of shear wave speed dispersion［J］.The Journal of the Acoustical Society of A-merica，2004，115(6):2781-2785.

［17］ Salameh N，Peeters F，Sinkus R，et al.Hepatic viscoelastic parameters measured with MR elastography:correlations with quantitative analysis of liver fibrosis in the rat［J］.Journal of Magnetic Resonance Imaging，2007，26(4):956-962.

［18］ Wang M，Palmeri M，Guy C，et al.In-vivo quantification of liver stiffness in a rat model of hepatic fibrosis with acoustic radiation force［J］.Ultrasound in Medicine and Biology，2009，35(10):1709-1721.

［19］ Leavens C，Williams R，Burns P，et al.The use of phase codes in ultrasound imaging:SNR gain and bandwidth requirement［J］.Applied Acoustics，2009，70(10):1340-1351.

［20］ Chen Siping，Zeng Sining，Wang Tianfu，et al.Numerical simulation on acoustic radiation force induced by ultrasonic coded excitation ［J］.Journal of Shenzhen University Science and Engineering，2011，28(2):165-171.(in Chinese)陈思平，曾思宁，汪天富，等.超声编码激励产生声辐射力的数值模拟 ［J］.深圳大学学报理工版，2011，28(2):165-171.