被动型星载氢钟H型气体电离模型及参数优化

王勇 邱实 李建清

（1东南大学仪器科学与工程学院，南京210096）（2东南大学空间科学与技术研究院，南京210096）

1 引言

被动型氢原子钟是实现氢原子钟小型化的主要途径，它体积、质量相对较小，且相对于其他小型原子钟具有无可比拟的中、长期稳定度，适用于卫星定位、导航、空间探测及天文观测等系统，可以提供超稳定度的标准频率信号［1］。氢气电离装置是被动型星载氢原子钟的重要物理部件，它将经过提纯器过滤后的纯净的氢气电离成为氢原子，以便经过选态以后产生高能态氢原子并注入到储存泡中，从而产生1.420GHz跃迁微波信号。

电离电源的功率不仅影响了小型氢钟的星载质量和体积，还决定了电离电磁能对整个电子系统的电磁干扰特性（电离振荡器功率越大，电磁辐射干扰越强）［2］。因此，优化电离参数从而降低电离功率是电离装置重要的设计目标。现有氢钟气体电离系统功耗较大且无理论模型，文献［2］给出了一种采用螺线管式馈能天线的电离装置，其频率在80～150MHz之间，功耗5～10W；文献［3］给出了一种直流磁场增强型感应耦合氢气电离装置，功耗2.5W。文献［4］给出了一种针对甲烷气体电离的射频感应耦合的电离仿真模型，但是针对被动型氢钟氢气感应耦合电离方式的电离数学模型、电磁场分布及电离规律有待进一步详细研究。

本文采用射频H型感应耦合电离方法，建立氢原子在电离泡中的电离及电磁场分布模型，给出电离击穿条件及电离规律，此方法为被动型星载小型氢钟的氢气电离过程的功率优化提供了理论依据，使得设计的电离装置功率较传统设计有所降低，电磁干扰特性得到改善。

2 氢气电离机制及电磁场分布模型

射频H型电离方法的氢气电离过程可以概括为：射频电流流过耦合天线，在天线周围先产生交变磁场，由交变磁场再感应出交变电场；氢气中存在的少量自由电子（约103／cm3）在射频电场的作用下加速而获得较高的平均动能；高速电子与氢分子发生非弹性碰撞产生能量转移，氢分子获得足够的能量而离解成两个氢原子，且放出光子和热量，通常可观测到电离泡中呈暗红色状态［2］，如式（1）所示

式中g＋为电离源施加给氢分子的电磁能量；h为普朗克常数；υ为放出光子的谱线频率。

电离系统设计原理如图1所示，采用图1（a）所示克拉拨三端振荡电路；并将电路中的振荡电感L1作为馈能天线，绕制成图1（b）中所示平面盘绕线圈，采用圆柱形电离泡，且平面盘绕线圈和圆柱形电离泡的底面同轴心安装。振荡电流在天线周围产生H型辐射场，即磁偶型辐射场，从而将射频电离振荡器产生的电磁能量馈入电离泡中的气体。

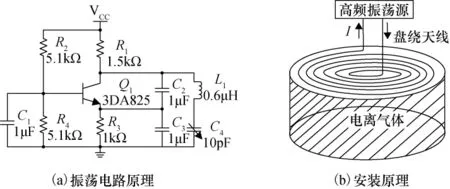
图1 电离振荡电路及射频H型感应耦合电离原理示意Fig.1 Ionization circuit and inductive coupling ionization principle for H-mode

设在平面盘绕天线中通入交变的电流为I＝I0exp（-jωt），I0为电流的振幅，ω为电流源振荡角频率。该电流在电离泡中产生的电磁场分布与电离泡中的气压、泡尺寸及电离源频率等均相关。把电离气体形成的等离子体作为有限电导率介质处理，由Maxwell方程可以得到圆柱形电离泡中的空间电磁场分布规律为［5］

式中E，B分别为电离泡中的电场强度和磁感强度；σ，μ，ε分别为电离氢气的电导率、磁导率和介电常数。由式（2）可以得到电离泡中电场和磁场满足的Helmholtz方程

式中ε′＝ε-jσ／ω。由于交变电磁场具有空间对称性，故电离泡中的电场和磁场可表示为

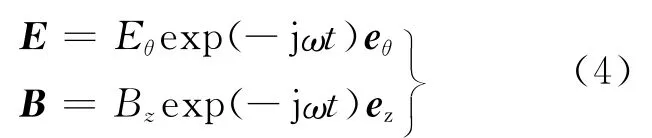
式中Eθ，Bz分别为电离泡中电场强度和磁感强度的幅值；ez，eθ分别为电离泡轴向z和横向沿θ方向的单位向量，如图2所示。

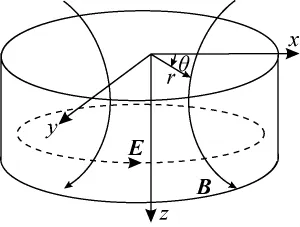
图2 电离泡中电磁场属性Fig.2 Electromagnetic field property in ionization bubble

将式（4）转换成柱坐标形式，则电离泡中的电磁场服从

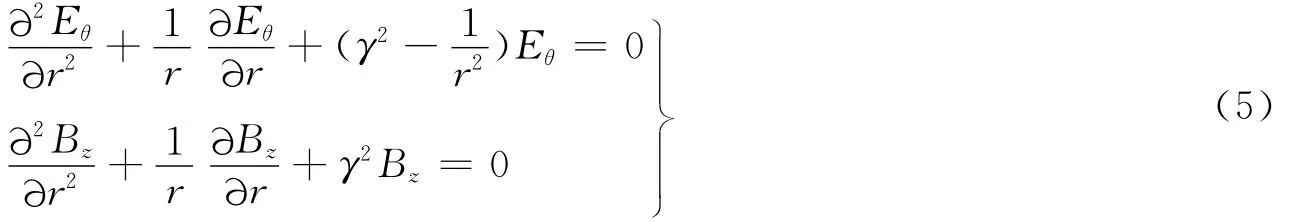
式中γ为电离气体对电磁波的传播常数，γ2＝ω2με′＝μεω2-jωμσ。式（5）分别为关于Eθ和Bz的一阶Bessel方程和零阶Bessel方程，求解方程得［5］

式中 0≤r≤R；R为电离泡的半径；ER，BR分别为r＝R处的电场强度和磁感强度；J0，J1分别为零阶Bessel函数和一阶Bessel函数。根据圆柱体电离泡内Maxwell方程的时域表达式可得

由Bessel函数的性质J′0（γr）＝-γJ1（γr），结合式（6），式（7）可得

式中B0为电离泡中心轴上的磁感强度。所以，式（3）可改写成［6］

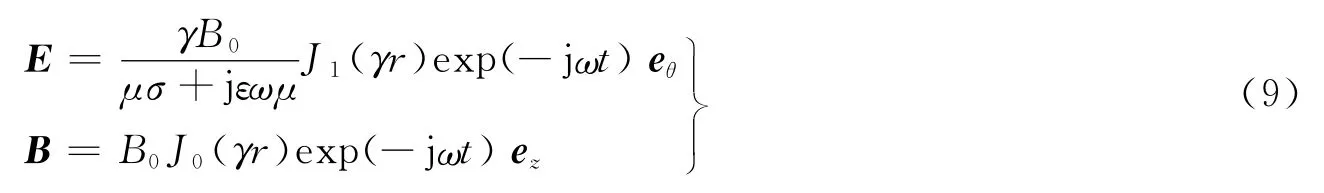
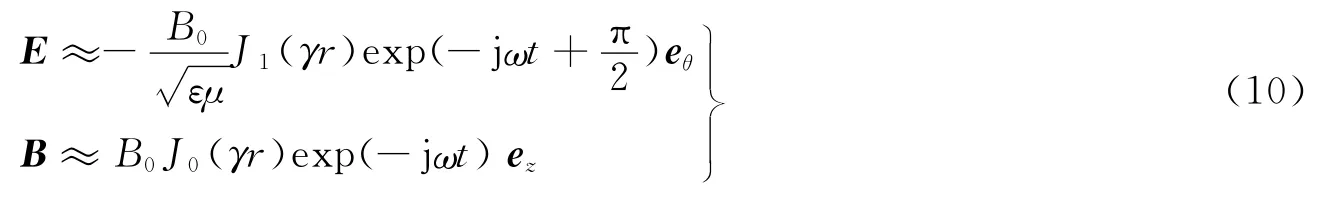
由式（10）可以看出，空间任意点电场强度Eθ滞后磁感强度Bz约π／2，且在半径r比较小（即r＜1／γ）的情况下，电离泡中心轴上磁感强度最大，电场强度接近于0，而在电离泡侧面处磁感强度最小，电场强度最大。

3 气体击穿条件及其数学模型

根据以上的物理模型可知，气体中的电子受到磁感B的洛伦兹力而沿轴心作圆周运动，且受到电场E的电场力而沿θ方向加速，从而获得足够的能量才能使氢气被电离。根据汤普逊放电理论，气体击穿条件要求电子在小于一个自由程的时间内从电场中获得的能量大于氢原子的电离能［7］。

由式（10）得到电子受到的沿θ方向的加速电场力大小为

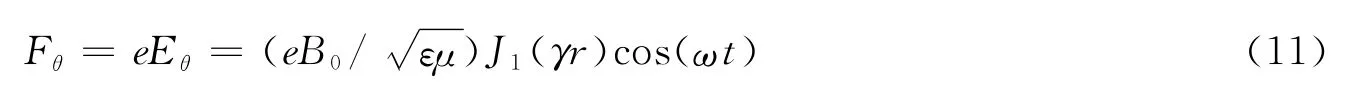
当γr很小时，有J1（γr）≈ （γr）／2，式（11）可简化为

由牛顿运动定律得到电子的运动方程为

式中m为电子的质量；v为电子做圆周运动的切向速度。求解式（13）得

式中C为常数，在击穿临界条件下C＝0，且在r＝R处，电子的运动速度可表示为

在r＝R处，电场强度最大，最易被击穿，这就要求其中，Vi是气体的电离电位；ve0是气体电离时被加速的电子须达到的最低速度［8］。在时间t内，r＝R处的电子运动的距离为

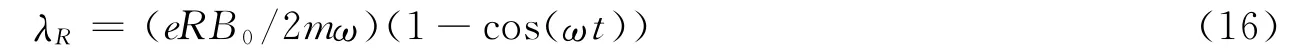
r＝R处气体电离的条件可表示为

即电离的临界条件为

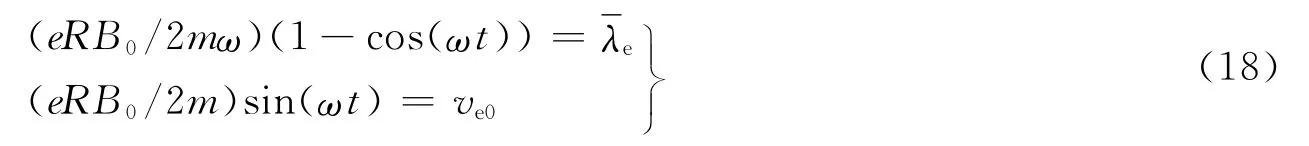
这就是氢气电离所要求的磁感强度B0（最小值）满足的数学模型——击穿判据。

4 氢气电离规律及参数优化

式（19）中B0是维持氢气电离的最小磁感强度，它由电离振荡器馈能天线中的电流产生，从而直接决定了电离电源的最小功耗。可以看出，B0与电离振荡器的角频率ω及电离泡中的气体电子的平均自由程（决定于单位体积内氢气分子数或气体密度N）相关。将式（19）中的B0对角频率ω微分可得

同理，将式（19）中的B0对平均自由程微分可得

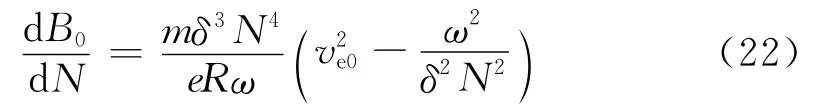
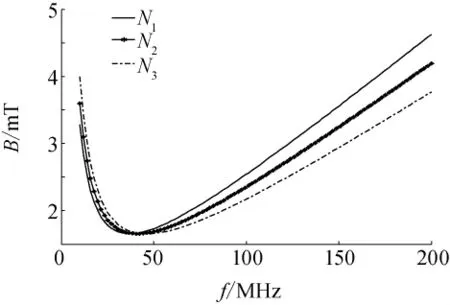
图3 氢气电离磁场与电离频率关系Fig.3 Relationship between electromagnetic field and the ionization frequency

图4 为一定电离频率下的电离磁场随电离泡中气体密度变化关系图，结合数学表达式和图4可以分析得出：在电离振荡器频率一定且电离泡中氢气密度增加但不超过N0的情况下，由于电离泡中的自由电子也随之增加，气体从电磁场中获得能量的能力增强，击穿氢气的电离电源的功率反而减小。

以上理论推导为实际系统优化设计提供了依据，实际设计的射频电离振荡器的频率取为f＝（2～3）f0，以控制电离电源的功率，使得电源功率足够小，且有足够的裕量以维持氢气电离，振荡器采用克拉拨三端振荡电路，合理选择其中电容，并设计制作适当的盘绕线圈天线即可设计固定频率f＝（2～3）f0的电离振荡器；而实际电离过程中气体密度较难精确测量与控制，一般采用控制钯银合金提纯器的温度来控制气体流量从而间接控制泡内气体密度，试验中也可以读取离子溅射泵的负荷电流（代表真空度）来间接反映电离泡中的气体密度大小。

利用以上的物理模型和电离规律，综合考虑各个参数之间的影响和矛盾，给出一组优化的感应耦合电离系统参数：电离泡体积为51.4mL，天线圈数为5圈，天线电感为0.6μH，电离频率为100MHz；并测得电离直流电源总功率小于2W，且电离泡呈玫瑰红色。

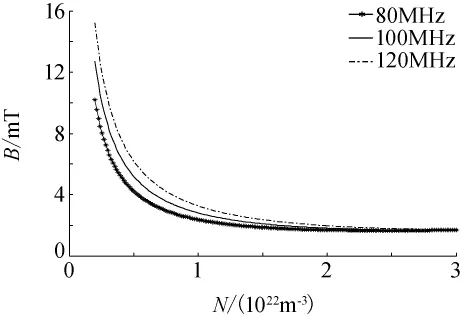
图4 N≪N0情况下，电离磁场与氢气密度关系Fig.4 Relationship between electromagnetic field and the gas density when N≪N0

图5 给出了根据优化参数设计的感应耦合电离系统电离功率随溅射离子泵负荷电流变化的实测曲线，该实测曲线与图4中的数值计算结果相对应，是电离频率一定且离子泵负荷电流（即气体密度）取值极低时的测试结果，实测结果验证了气体密度和电离功率的理论关系，实际真空泵的负荷需根据原子信号增益的要求适当调整，但在负荷满足要求的情况下（100～600μA）电离直流电源总功率可小于2W，可以看出，应用该理论模型和优化参数较传统的设计结果更加理想。进一步分析可知：在气体密度很低的范围内可以适当提高气体密度来提高自由电子密度，以提高气体对射频电磁能量的吸收效率，从而可以降低电离功率；需要指出的是，气体密度还受原子增益要求、真空泵的寿命、电离源的可靠起辉，以及存储泡的饱和度等因素的限制，在整机调试过程中还要综合考虑这些因素来决定电离泡中气体的密度，但该理论模型和电离规律为电离系统的功率优化提供了一种方法和思路。

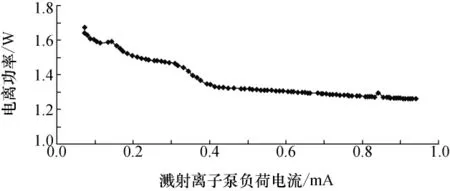
图5 电离功率随溅射离子泵负荷电流变化的实测曲线Fig.5 Measured curve of the relationship between the ionizing power and load current of the sputter ion pump

5 结束语

本文设计了被动型星载氢钟H型射频感应耦合气体电离系统，推导出了电磁场分布模型及电离击穿条件的数学模型，并研究了其电离规律，优化了设计参数，可以得到如下结论：

1）这种射频H型电离方式中的电场和磁场相互正交，磁场沿电离泡轴向z方向，而电场沿电离泡横向θ方向，且电离泡中心轴上磁感强度最大，电场强度接近为0；而在电离泡半径较小的情况下，电离泡外侧磁感强度最小，电场强度最大。

2）要使电离泡中的氢气电离击穿，要求磁感强度达到最小值B0，B0与电离振荡器的角频率ω及电离泡中单位体积内氢气分子数N有关。

3）射频电离一般需要很高的电离频率，而为了达到被动型氢钟小型化和降低电磁辐射的目的，要使电离的功耗得到优化，这里给出了一种选取方法，即在电离泡中气体密度一定的情况下，作为维持氢气电离的临界频率，而选取射频电离振荡器的频率为f＝（2～3）f0以控制电离电源的功率，使得电源功率足够小，且有足够的裕量以维持氢气电离。

4）被动型氢钟电离泡中的气体密度处于极低的范围内，电离泡中气体密度可适当增加，从而降低电离功率，此外，还要综合考虑原子增益大小、整机的寿命、电离源的可靠起辉等因素决定氢气流量和电离泡中的气体密度，这些影响因素及其规律有待进一步研究。

［1］王勇，李建清，邱实.被动型氢原子钟储存泡口原子分布计算及应用 ［J］.东南大学学报：自然科学版，2012，42（1）：67-71.WANG YONG，LI JIANQING，QIU SHI.Calculation of atoms distribution at storage bubble entrance of passive hydrogen maser and its application ［J］.Journal of Southeast University：Natural Science Edition，2012，42（1）：67-71.

［2］RIEHLE F.Frequency standards［M］.Weinheim，Germany：Weily-VCH，2004：229-252.

［3］MALEKI L.The development of a magnetically enhanced hydrogen gas dissociator［C］.36th Annual Frequency Control Symposium，Philadelphia，June 2-4，1982.New Jersey：IEEE，1982.

［4］BERA K，FAROUK B，VITELLO P.Inductively coupled radio frequency methane plasma simulation ［J］.Journal of Physics D：Applied Physics，2001，34（10）：1479-1490.

［5］唐平瀛，丁伯南，戴晶怡.高频H型放电离子源的场特性 ［J］.强激光与粒子束，2003，15（9）：932-936.TANG PINGYING，DING BONAN，DAI JINGYI.Characteristics of RF ion source electromagnetic field ［J］.High Power Laser and Particle Beams，2003，15（9）：932-936.

［6］ROBERTSON S，KNAPPMILLER S，STERNOVSKY Z.Energy balance and plasma potential in low-density hot-filament discharges［J］.IEEE Transactions on Plasma Science，2006，34（3）：844-849.

［7］王超，熊熠明，李培芳.感应耦合气体放电及其静电场 ［J］.真空电子技术，2003（1）：18-20.WANG CHAO，XIONG YIMING，LI PEIFANG.Inductively coupled gas-discharge and its electro static field ［J］.Vacuum Electronics，2003（1）：18-20.

［8］TOADER E I，COVLEA V N.Enhanced magnetic ionization in hydrogen reflex discharge plasma source［J］.Review of Scientific Instruments，2005，76（3）：033502-4.