基于径向基神经网络的双馈风力发电机低电压穿越控制研究
邱道尹,张凌云,顾 波,李晓丹
(华北水利水电大学,河南 郑州450045)
风能作为一种清洁、可再生能源,越来越受到全球范围内的广泛关注.近年来,我国风电事业的发展突飞猛进,风电装机容量不断攀升.由于风速具有波动性和间歇性,导致了大容量的风电并网对电网电压稳定产生较大的影响,必须采取有效的低电压穿越控制措施,以确保风电并网的稳定性[1-2].
风电场的低电压穿越(LVRT)是指,在电网故障期间风电机组端电压跌落,风机能够在一定时间范围内保持并网不间断运行,甚至向电网提供一定的无功功率,支持电网恢复,从而穿越这个低电压区域.在各种类型的风力发电机组中,双馈感应风力发电机(DFIG)以其调速范围宽、有功和无功能够解耦控制以及变流器容量较小等优点,成为国内外应用广泛的风电机组类型之一.目前,对电网电压跌落故障下提高DFIG 机组的LVRT 能力,已成为国内外专家学者的研究热点[3-7].
文献[8]中提出了采用无功补偿的方案来实现风电机组的LVRT 功能,以满足风电并网对LVRT能力的要求;文献[9-10]中针对双馈风电机组,在电网故障时采用增加硬件Crowbar 卸荷电路,有效提高了双馈风机的LVRT 能力;文献[11]通过在双馈风机直流侧增加卸荷电路来吸收多余能量,达到稳定电压的目的;文献[12]中提出了利用串联制动电阻来提高风电场LVRT 能力的方法;文献[13]设计了TS 模糊PI 控制器,有效抑制了电网故障时双馈风力发电机有功功率和变流器直流母线电压震荡,从而提高系统的LVRT 能力;文献[14]采用灭磁方式实现DFIG 风电机组的故障不脱网运行.
常规的PI 控制以其结构简单、可靠性高等优点被广泛采用.但当被控对象存在强干扰,具有高度非线性和不确定性时,仅靠PI 调节效果不好.因此,提出了一种基于径向基(RBF)神经网络在线辨识的PI 控制器自适应控制算法,利用RBF 神经网络进行在线辨识,并根据被控对象的Jacobian 信息在线调整PI 控制器参数.建立了双馈感应电机完整的5 阶数学模型,分析了其电流模式控制方案.针对所提出的基于RBF 神经网络辨识的PI 控制器自适应控制算法,搭建Simulink 仿真模型. 仿真结果表明,将RBF 神经网络与PI 控制器相结合的自适应控制策略有效抑制了由电压跌落引起的电流震荡,缩短了系统故障恢复时间,动态性好,具有较好的自适应性和鲁棒性,提高了系统的低电压穿越能力.
1 基于DFIG 的风电机组模型
1.1 DFIG 数学模型
DFIG 采用绕线式感应发电机,其定子绕组通过变压器与电网相连,转子绕组通过背靠背可变频电压源变流器供电. 该变流器一般由2 个基于IGBT的AC/DC 电压源变流器(VSC)组成,两变流器之间通过一个直流环节连接. 直流链节中的电容器将2个VSC 解耦,从而使得这两个变流器能够受到独立的控制.故变流器对电网频率和转子机械频率的解耦作用实现了双馈电机的可变速运行. 常见的基于DFIG 风电机组的典型结构如图1所示.

图1 风电机组的拓扑结构
为了便于分析和控制,通常将ABC 三相静止坐标系下DFIG 的复杂模型转换为两相d-q 同步旋转坐标系下的简化模型. 常见的双馈感应电机模型有8 阶、5 阶、4 阶和忽略定子电瞬变的3 阶模型[15-17].此处采用5 阶数学模型,方程中除同步速以外的所有参数均以标幺值的形式给出.具体如下:

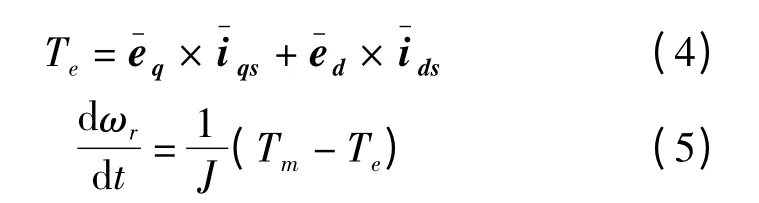
1.2 DFIG 控制方案
DFIG 的动态调节是通过背靠背功率变流器实现的.通常,由转子侧变流器实现转矩控制、机端电压控制以及功率因数控制,由电网侧变流器维持母线电压恒定.
DFIG 的电气控制通常采用电流控制模式,控制方案中将转子电流分解为d 轴和q 轴2 个正交分量.其中,电流的d 轴分量用来实现机端电压或功率因数的调节,电流的q 轴分量用来调节转矩.
1)转矩控制方案.转矩控制器根据风速的变化调节发电机的电磁转矩,以跟踪最大功率曲线使风电机组运行在期望参考点上,从而在风力中捕获到最大功率.设已知转子转速的测量值,根据风力机的最大功率捕获特性可得转矩参考值Tsp,进而计算出转子电流q 轴分量参考值iqrref.忽略定子电阻和定子暂态,采用定子磁链定向(SFO)的参考坐标系,定子电压的d 轴分量=0,故有
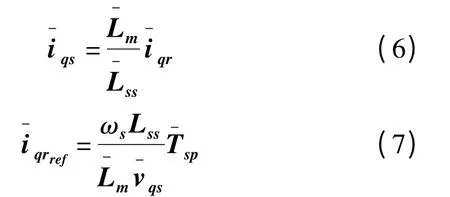
2)电压控制方案.该控制方案一般采用转子侧变流器来实现机端电压控制或功率因数控制. 考虑电网侧的无功功率,忽略定子电阻,且采用SFO 参考坐标系有
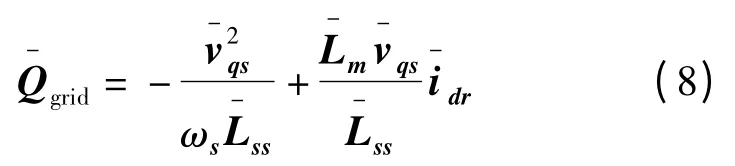

图2 DFIG 转矩控制方案
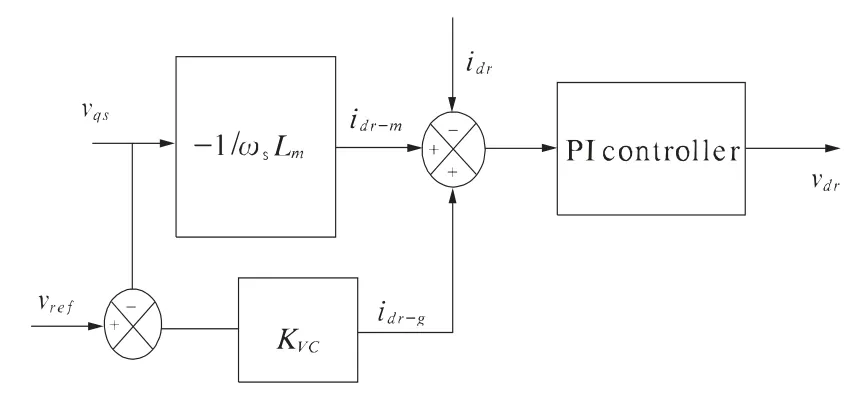
图3 DFIG 电压控制方案
2 基于RBF 神经网络辨识的PI 控制器设计
2.1 RBF 网络结构
RBF 神经网络是一种单隐层的3 层前馈网络,其基本结构如图4所示. RBF(Radial Basis Function)网络模拟了人脑中局部调整、相互覆盖接收域的神经网络结构,是一种局部逼近网络,可以证明它能够以任意精度逼近任意连续网络. 与BP 网络相比,由于RBF 网络从输入到输出的映射是非线性的,而隐层空间到输出空间的映射是线性的,从而大大加快了学习速度,并避免了局部极小的问题[18].

图4 RBF 神经网络结构图
在RBF 神经网络结构中x1,x2,…,xn为输入,ym为输出,ω1,ω2,…,ωm为权值.设RBF 网络径向基向量

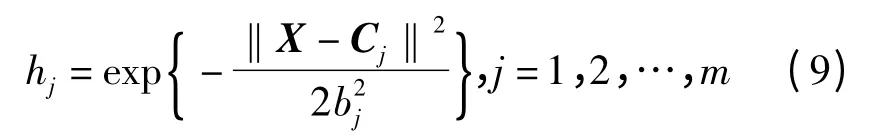
式中:hj为高斯基函数;Cj为网络的第j 个节点的中心矢量
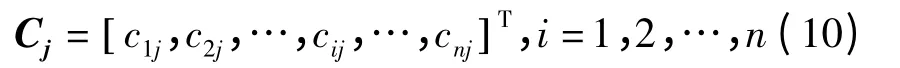
设网络的基宽向量为

式中bj为节点的基宽度参数,且bj>0.
k 时刻网络的输出为
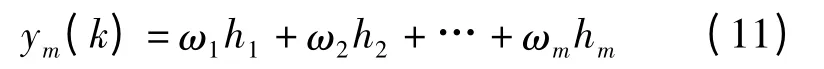
设理想输出为 y (k) ,则辨识器的性能指标函数为

根据梯度下降法,输出权、节点中心及节点基宽参数的迭代算法分别为:
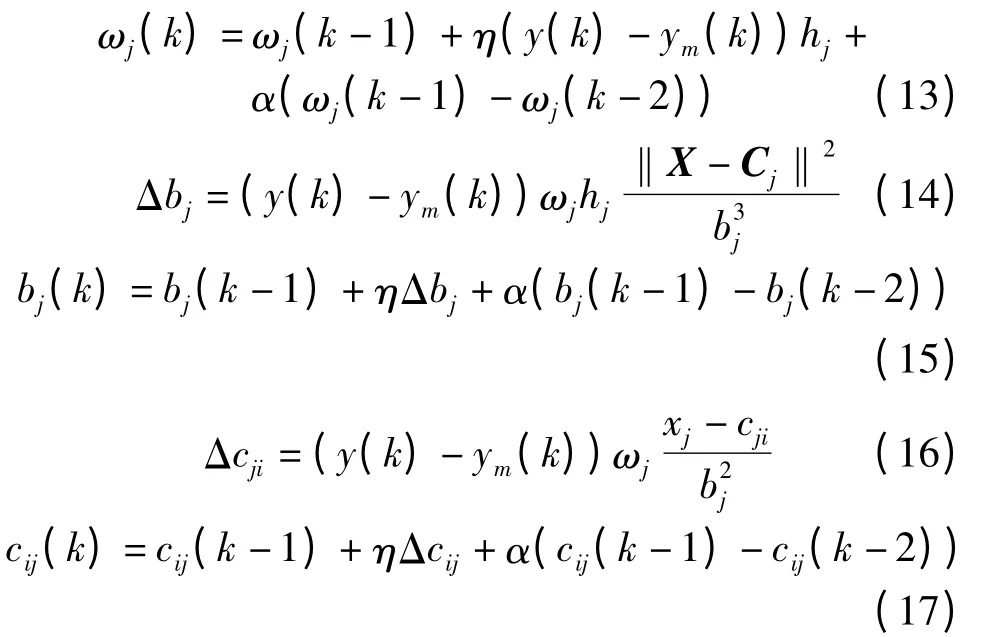
式中:η 为学习速率;α 为动量因子.
Jacobian 阵(即对象的输出对控制输入的灵敏度信息)算法为

式中x1=Δu(k)=u(k)-u(k-1).
2.2 基于RBF 神经网络的PI 控制器自适应原理
图5为基于RBF 神经网络的PI 自适应控制原理图.将RBF 神经网络与传统PI 控制相结合,分别以转子d 轴和q 轴电流为被控对象,由RBFNN 辨识器对被控对象进行在线辨识,并根据辨识出的Jacobian 信息在线调整PI 控制器的参数,从而实现对被控对象的快速准确控制.

图5 基于RBFNN 整定的PI 控制器
PI 控制器采用增量式算法,设控制误差为
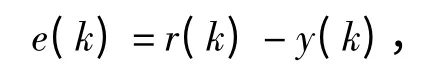
式中r(k)和y(k)分别为采样时刻k 的输入和输出.
PI 控制器的两项输入为

则PI 控制器的输出为
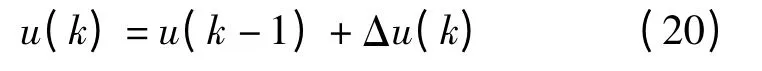
式中:Δu(k)=KP(k)x1(k)+KI(k)x2(k);KP(k),KI(k)分别为比例和积分系数.
设RBF 神经网络整定控制器的性能指标函数
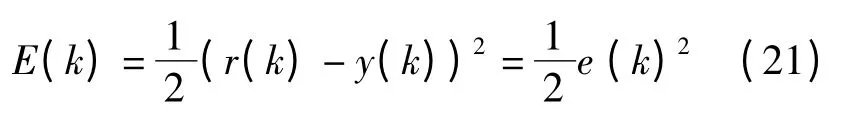
采用梯度下降法,调整KP(k),KI(k),有
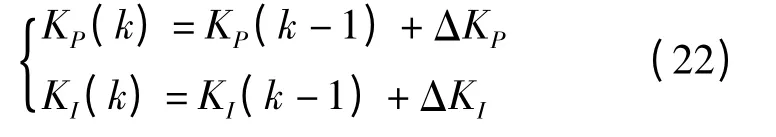
式中:
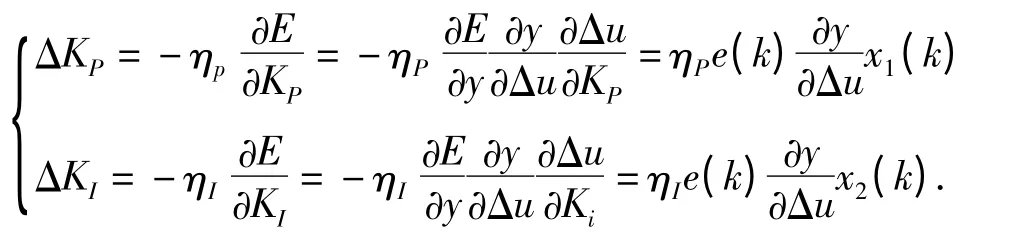
综上所述,基于RBF 神经网络的PI 控制器自适应控制算法步骤可归纳如下.
1)确定RBF 网络的中心矢量、基宽参数、学习速率、惯性系数和PI 控制器参数KP,KI的初始值.
2)采样获得系统的输入r(k)、输出y(k)和控制误差e(k),通过计算得到网络的输入信号x1(k),x2(k),调整RBF 网络的权值,得到网络输出的Jacobian 信息.
3)根据获得的Jacobian 信息调节PI 控制器的参数KP,KI,并计算控制器的输出u(k),同时将其送给被控对象和RBF 网络,产生下一步的实际输出和辨识输出.
4)k=k+1,返回步骤2,直到获得满意结果.
3 仿真分析
为了验证该控制方案的有效性,根据DFIG 风电机组系统结构及工作原理搭建Simulink 仿真模型,如图6所示.以2 MW 的DFIG 风力发电系统为研究对象,DFIG 选用绕线式异步电机5 阶模型,仿真参数为:额定功率2 MW,额定电压690 V,额定频率50 Hz,定子电阻0.004 88 pu,定子漏抗0.092 41 pu,转子电阻0.005 49 pu,转子漏抗0.099 55 pu,励磁电抗3.952 79 pu,惯性时间常数3.5 s;风速恒定为11 m/s,故障发生时间为20 s,分机端电压跌落到故障前的20%和40%两种情况,故障持续时间0.2 s;仿真中,DFIG 转矩和电压控制方案中采用基于RBF神经网络的PI 控制器自适应控制算法,RBF 网络的学习速率η=0.2,惯性系数α =0.04,权值的初始值取[-1,1]上的随机数.
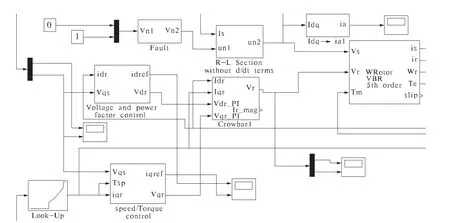
图6 DFIG 低电压穿越仿真结构图
将故障发生时的转子电流分别采用传统的PI控制和基于RBF 神经网络辨识的PI 控制器自适应控制算法的控制方案作对比.图7为电压跌落20%时转子d 轴电流的变化情况,实线表示系统在低电压穿越过程中采用传统PI 控制方案时的转子d 轴电流的变化过程,虚线表示采用基于RBF 神经网络辨识的PI 控制器自适应控制算法在低电压穿越时的转子d 轴电流的变化过程.由图可知,相比于传统PI 控制方案,采用基于RBF 网络的PI 控制器自适应算法使得转子电流震荡强度有了较明显的削弱,减小了震荡电流对转子侧变流器的冲击,保护了转子侧变流器,实现了对DFIG 的LVRT 控制.

图7 电压跌落20%的转子d 轴电流Idr变化曲线
图8是电压跌落20%时,转子q 轴电流的变化情况.图中实线和虚线分别为采用传统PI 控制方案和采用基于RBF 神经网络的PI 参数自整定算法时的转子q 轴电流在LVRT 过程中的变化曲线. 从图中可知,电压跌落时,采用基于RBF 网络辨识的PI控制器自适应算法有效地削弱了转子q 轴暂态电流峰值,保护了转子侧变流器,同时震荡电流的收敛速度更快,缩短了系统故障恢复时间.

图8 电压跌落20%的转子q 轴电流Iqr变化曲线
此外,由于电压跌落时发电机的电磁转矩迅速变小而机械转矩不变,导致了发电机转子转速迅速上升,对风力机转轴系统的机械应力造成冲击. 因此,通过对DFIG 的q 轴电流发生突变的有效抑制,可减小机组在LVRT 过程中的震荡,有利于延长机械系统的寿命,保证系统的平稳运行.
图9为电压跌落40%时,转子d 轴电流的变化情况.由图可知,随着电压跌落程度的加深,转子d轴电流波动幅度加大,震荡加剧. 与传统PI 控制器相比,采用基于RBF 网络辨识的PI 控制器自适应算法能够有效地抑制转子d 轴电流震荡. 表明该控制算法能及时跟踪被控对象的动态变化,并对PI 参数作出调整,实现对转子电流的有效控制,保护了转子侧变流器,提高了系统的自适应性和鲁棒性.

图9 电压跌落40%的转子d 轴电流Idr变化曲线
图10 为电压跌落40%的情况下,转子q 轴电流的仿真结果图. 由图可知,在基于RBF 神经网络的PI 控制器自适应算法下,转子暂态电流峰值明显削弱,保护了转子侧变流器,减小了由于转矩上升造成的对风力机转轴系统的机械应力冲击,延长了系统寿命,维护了系统的稳定运行. 此外,电流震荡收敛时间明显缩短,系统故障恢复时间有效减小.
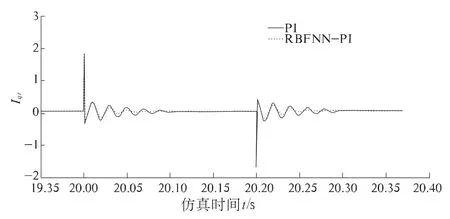
图10 电压跌落40%的转子q 轴电流Iqr变化曲线
4 结 语
基于RBF 神经网络辨识的PI 控制器自适应控制算法在电网电压跌落时能够有效地削弱转子震荡电流,保护了转子侧变流器,减小了对风力机转轴系统的机械应力冲击;同时,电流震荡的收敛速度明显加快,缩短了系统的故障恢复时间.通过采用新的控制算法,实现了PI 参数的自适应调整,从而达到了更高的控制精度,增强了系统的自适应性和鲁棒性,提高了系统的低电压穿越能力.
[1]牛山泉.风能技术[M].刘薇,李岩,译.北京:科学出版社,2009.
[2]Tony B,Nick J,David S. Wind Energy Handbook[M].UK:A John Wiley and Sons,Ltd.,Publication,2001.
[3]Anca D H,Lars H H. Wind turbine concept market penetration over 10 years(1995—2004)[J]. Wind Energy,2007,10(1):81-97.
[4]Clements J,Julija M,Thomas A,et al. International comparison of requirements for connection of wind turbines to power systems[J].Wind Energy,2005,8(3):295-306.
[5]Vicatos M S,Tegopoulos J A. Transient state analysis of a doubly-fed induction generator under three phase short circuit[J]. IEEE Transaction on Energy Conversion,1991,6(1):62-68.
[6]Johan M,Sjoerd W H de H. Short-circuit current of wind turbines with doubly fed induction generator[J].IEEE Transaction on Energy Conversion,2007,22(1):174-180.
[7]Dittrich A,Stoev A.Comparison of fault ride-through strategies for wind turbines with DFIM generators[C]//2005 European Conference on Power Electronics and Applications,2005.
[8]Chai C,Chitra Y,Kittipong M.Reactive compensaton techniques to improve the ridethrough capability of wind turbine during disturbance[J]. IEEE Trans on Industry Applications,2005,41(3):666-672.
[9]张学广,徐殿国.电网对称故障下基于active crowbar 双馈发电机控制[J].电机与控制学报,2009,13(1):99-103.
[10]Datta R,Ranganathan V T. Variable-speed wind power generation using double fed wound rotor induction machine-a comparison with alternative schemes[J]. IEEE Trans on Energy Conversion,2002,17(3):414-421.
[11]Abbey C,Joos G. Effect of low voltage ride through(LVRT)characteristic on voltage stability[C]//IEEE Power Engineering Society General Meeting,San Francisco,2005.
[12]王虹福,林国庆,邱家驹,等. 利用串联制动电阻提高风电场低电压穿越能力[J]. 电力系统自动化,2008,32(18):81-85.
[13]王兴贵,夏岩,马呈霞,等.基于TS 模糊控制的双馈风力发电机低电压穿越技术研究[J]. 电力系统保护与控制,2011,39(12):7-10.
[14]Xiang D,Ran L,Tavner P J,et al.Control of a doubly fed induction generator in a wind turbine during grid fault ride-through[J]. IEEE Transactions on Energy Conversion,2006,21(3):652-662.
[15]Olimpo A,Nick J,Janaka E,et al. Wind Energy Generation:Modelling and Control[M]. UK:A John Wiley and Sons,Ltd.,Publication,2009.
[16]Iulian M,Antoneta I B,Nicolaos-Antonio C,et al.Optimal Control of Wind Energy System[M].UK:Springer-Verlag London Limited,Publication,2008.
[17]胡家兵,孙丹,贺益康,等. 电网电压骤降下双馈风力发电机建模与控制[J]. 电力系统自动化,2006,30(8):2l-26.
[18]Bors G,Pitas I. Median radial basis function neural network[J].IEEE Transactions on Neural Networks,1996,7(6):1351-1364.

