Comparison of Three Brine Migration Models in Groudwater

Yu Liu

Ph.D, Hydrogeology Department, Faculty of Geology,Moscow State University, sail526@mail.ru

Abstract: Three brine migration models in underground waters were compared to solve the problem of high-density brine migration in underground fresh waters. As shown by the example of brine occurrence in salt dumps, it is preferable to use the model of variable-density solution migration for real layered hydrogeological systems.

Keywords: brine migration； variable density

Introduction

Forecasting of the brine migration that enters underground waters from salt dumps was conducted using mathematical modeling methods.There are several approaches to modeling brine migration. Methods usually take into account variations in brine density, caused by the mixing of fresh ground water with concentrated brine. This processes leads to the formation of a contamination area, which consists of a heavier nucleus of slightly diluted concentrated brines and surrounding salty waters that change the salt concentration to the natural level with distance from the nucleus (Mironenko et al. 1988).

However, there is another way to model concentrated brine: flows of underground waters are fluidic, and brine is scarcely diluted by fresh waters and thus is an immiscible heavy liquid that submerges in light fresh waters (Konyukhov et al.1998). Dispersion of brine concentration on the nucleus border is caused by partial infilling of pores by only brine or only fresh water(Konyukhov et al. 2002).

Konosavsky et al. (2002) conducted a comparative analysis of methods used for homogeneous migration and obtained a good agreement of results. However, these methods yield significant data discrepancies for ordinary hydrogeological layered systems. To adequately imitate the dissolved salt distribution, it is necessary to thoroughly divide the migration space into modeling blocks (Konosavsky et al. 2002). It is virtually impossible to conduct such detailed modeling using real models and personal computers due to the long processing time that is needed for the solution of nonlinear problems. As a result, brine migration was investigated using a realistic filtration scheme with ordinary and even more that normally detailed discretization of the modeling area.

Modeling of brine migration

The methods were compared using the Seep-Ctran complex ( Krakn 2004) and FILTRF programs (Konyukhov et al. 1998). The first program was used to display ordinary migration of miscible liquids excluding variable density and taking the variable density of groundwater in a finite element representation into account, while the second program was applied to display the model of immiscible variable-density liquid migration.

The cross section of the groundwater flow passing through the crossing salt dump at the southern end of Solikamsk was taken as the basis for a model scheme to compare the methods.

The chosen cross-section is 4,400 m in length,the distance from its western part to the salt dump is 40 m, and the salt dump is 660 m in width. Four layers with relatively homogeneous parameters were distinguished on the basis of a hydrogeological description (Migunov 1994；Mironenko et al. 1988) (Fig. 1): (1) the water-bearing layer of fluvial, largely sand,deposits is 20 m in thickness； (2) the water-bearing limestone layer of the Upper Solekamsk level or terrigenous carbonate rock sequence is 26 m in thickness； (3) the relatively impermeable clay limestone layer of the terrigenous carbonate rock sequence is 86 m in thickness； and (4) the pore water bearing layer of the Lower Solikamsk water-bearing level or saline-marl rock sequence is 42 m in thickness. The average western dip of the layers is 10°.

On the eastern border of the model, the water height is taken as 108.5 m (due to the conditional influence of the Kama River), while the western border is impermeable. The Infiltration of brine in the salt dump reaches 0.0014 m/day. In the eastern part of the salt dump there is an area with an infiltration of 0.0001 m/day that is 2,000 m in length. The salt concentration in the water entering from the salt dump is 360 g/l at a density of 1.2 kg/l. The salt concentration in the natural waters is taken as zero at their density of 1 kg/l. The filtration parameters and active porosity of the layers are shown in Fig. 1.

The modeling area consists of 99 blocks lengthwise and 30 blocks from top to bottom, with 3,366 blocks in all. The first layer was divided vertically into 4 blocks； the second layer, into 5 blocks； the third layer, into 17 blocks； and the fourth layer, into 8 blocks. This model is thought to be a pattern that differs from real hydrogeological conditions.

Area of migration, sampling, field of parameters and boundary conditions were identical for the three methods of modeling.

Fig. 1. Numerical model with geofiltration parameters:(1) sand, (2) limestone, (3) clay limestone, (4) marl clay with gypsum.

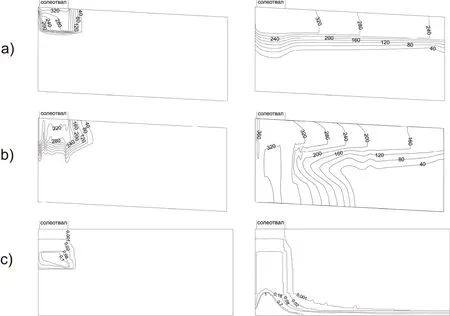
Fig. 2. Brine migration paths compared by three methods: (a) - excluding variable-density solution migration,Seep-Ctran complex； (b) - variable-density solution migration, Seep-Ctran complex； (c) - immiscible liquid migration, FILTRA program. On the left, 365 days, on the right, 7300 days.

Results of modeling

The results of modeling by the three meth ods are shown in Fig. 2. It should be noted that at the initial stage of modeling the form of brine migration under the salt dump is similar in models:the brine column descends almost vertically. In the model excluding variable-density, solution migration mostly occurs in the horizontal direction,ie, the second layer and the top of the third layer.In the vertical direction, brine migration to the middle of the third layers has stopped. In the model of variable-density solution migration, the third impermeable layer, over which the gradually diluting brine is spreading, plays an important role in the distribution of dissolved salt. In the model of immiscible liquids, an absolutely impermeable bed,at the foot of the last (fourth) layer, is required to change the migration direction from vertical to horizontal. In spite of the fact that permeability decreases when brine migrates from the upper layer to the lower one, the horizontal permeability of the first and second layers is 20-25 higher than that of the third layer.

Conclusions

One disadvantage of the immiscible liquids model is the lack of mixing at the contact of fresh water and brine. As a result, the contamination nucleus is always characterized by maximum density and moves strictly downwards. The main advantage of this model in the FILTRF program is the ability to describe it efficiently under the penetration of a heavy displacement fluid into the area that was initially occupied by less dense water with virtually constant permeability in depth.

The data from inspection wells in the nearest salt dumps of the Solikamsk-Berezniki district show insignificant contamination far from the boundaries of salt dumps and an increase in contamination at depth (Mironenko et al. 1988).Thus, it is preferable to apply the modeling method based on variable-density salt migration.