运用物理学史方法建立闭合电路欧姆定律

杨凤娟 郭玉英

（1.北京师范大学大兴附属中学，北京 大兴 102600；2.北京师范大学物理系，北京 100875）

1 引言

自上个世纪80年代开始，在我国物理课程与教学论领域，把物理学史引入物理教学的呼声越来越高，研究成果不断涌现.综观这些研究，对于物理学史教育的价值、意义、作用阐述较多，而具体实施方法研究较少；在物理学史的教学建议上，原则性阐述较多，操作性研究较少；在中学物理教学实践中，局限于牛顿第一定律、原子的核式结构等写入教材的经典学史教学案例较多，主动开发没有写入教材的学史方法建立概念、规律的教学案例较少.

有一份对某地区高中物理教师的调查显示：只有24.1%的教师经常在物理教学中融入物理学史内容，有62.9%的教师偶尔在教学中融入物理学史内容，有13.0%的教师在物理教学中基本不融入物理学史内容.而融入的深度又如何呢？有研究显示：教学中引入物理学史仍处于“某某科学家某某年发现或提出了……”这样的水平上，通常采用的模式是：旧理论的困难→假说的提出→假说的实验验证，而对困难是什么，假说提出与实验验证的过程没有详细展开分析讨论，只是一语带过，留给学生的是一笔糊涂账.真正带领学生遵循物理学史方法建立概念、规律的教学尝试真的是少之又少.

这表明，把物理学史引入中学物理教学的实践研究大有可为，期待一线教师更加主动、更强意识的教学探索.而教师的教学探索不仅需要“应然性”的理论思辨，更需要“实然性”的知识储备和案例启发，所以本文先简述欧姆发现闭合电路欧姆定律的历史过程，然后以笔者运用学史方法建立闭合电路欧姆定律的真实教学案例，启发教师的实践灵感，认识物理学史的重要教育价值，促进中学物理教学引入物理学史从“量”的积累到“质”的飞跃.

2 欧姆建立闭合电路欧姆定律的历史回顾

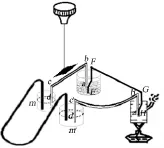
图1

首先明确一点，欧姆发现的是闭合电路欧姆定律，而不是部分电路欧姆定律.他当年为了研究电路规律设计了这样的实验方案（如图1所示）：EFGH 是一个用金属铋制成的∏型框架，框架每条腿上各铆接一个铜框abcd和a′b′c′d′，2个铜框的另一端分别浸在盛有水银的杯子m和m′中，用来连接外部的被测导线.当时没有检流计，智慧的欧姆受库仑扭秤的启发，设计了丝悬磁针电流计，用悬挂在铜框上方的小磁针偏转角度间接测量电流的大小.铜铋框架铆接好的两端分别插入沸水和冰水混合物中，组成发电性能稳定的温差电池.实验时将测试用的导线插在m和m′间，随着导线成倍数的加长，欧姆观察记录了小磁针的偏转角度，并把这些角度与对应的被测导线长度制成表.1826年1月8日，欧姆得到如下数据见表1.

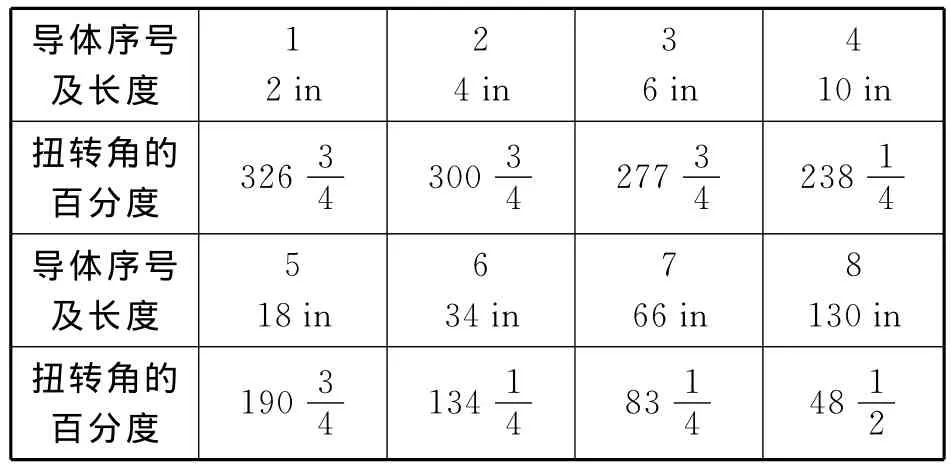
表1

仔细研究表格数据之后，欧姆提出了一种猜想：以上数据能够十分满意地以等式描述，X是长度为x的导体的磁效应强度，a和b是依赖于激发力和电路其余部分的常数.在这个猜想之下，他用表中的数据确定了b的值为，并根据表中的一组测量值，算出a的值为7285，又用确定出的a、b的值对其他被测导体的数据进行了检验，与实际测的角度数非常近似.例如对3号导体，长度为6in，计算出的X值为277.53，而测量值为.在该月的11号和15号两天，他每天取两组以上的数据做上面的分析.后来，他又保持铜线长度不变，改变温差，发现X和温差成正比关系.总之，经过反复实验，公式是令人满意的.于是，新的定律建立了.我们现在可以判断：欧姆的a相当于电动势，b相当于除待测导体以外其余部分的电阻，X相当于电流强度.欧姆的这一结果在1826年发表.

从发现史来看，闭合电路欧姆定律是一个基于实验的科学发现的过程，并非是一个演绎推理的结果，所用的逻辑思维以及数学表征工具是高二学生完全可以理解和应对的.那么，教学中可否遵循欧姆发现定律的实验和思维历程建立闭合电路欧姆定律呢？从高二学生现有的知识基础和能力现状出发该怎样设计和引导呢？于是，笔者从对学生的个别教学调研开始尝试用物理学史方法建立闭合电路欧姆定律.经过对个别教学调研结果进行反思、调整，生成比较成熟的教学设计，然后到班级授课.从个别教学调研到班级授课的实践研究结果显示：欧姆发现定律的实验思想、思维逻辑完全可以被高中学生普遍接受，用学史方法建立闭合电路欧姆定律的教学设计是可行的、有效的，并且，在对学生进行科学研究方法与创新能力、人文精神的教学上还有独到的优势.

下面是笔者班级课堂教学实录的整理.实验所用电流表为演示用J0416型数字测试仪如图2，选用200mA量程时等效内阻为5.4Ω；电源为1节较新的5号干电池，内阻约0.7Ω；电阻箱为J2361型0－999.9Ω简式电阻箱，最小步进值为0.1Ω；自制的实验架，旨在把平面实验竖起来，便于学生观察.

图2

3 学史方法建立闭合电路欧姆定律的教学设计与实施

环节1.认知冲突，引入新课.

师：（边实验边对话）我们来看一个电路如图3，闭合开关，电路中有了电流，改变电阻箱的接入阻值，电流大小随之变化.电流I的大小随电阻箱阻值R按怎样的规律变化呢？根据是什么？

生：按反比规律变化，根据是欧姆定律.

师：咱们现在采集5组数据，看一看电流I随电阻箱接入阻值R的变化情况.请学生协助往Excel里输入数据，表2是某次上课实验的数据.

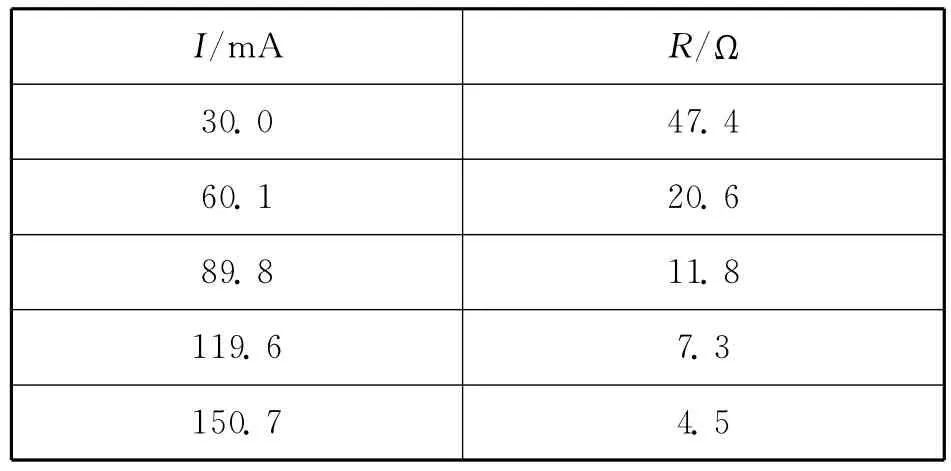
表2

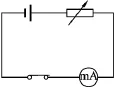
图3

师：I随R按什么规律变化？

生：反比关系.

师：为什么是反比关系？

生：因为电阻变小，电流变大，所以成反比.

师：什么是反比？

生：一个量变为几倍，另一个量就变为几分之一.

师：仔细观察一下表格中的数据，是这样的么？

生：看起来不是.学生小声回答，不太整齐.

师：如果I与R成反比的话，在I随R变化的过程中，IR的乘积是否变化？

生：不变.

师：那我们就用Excel计算一下I与R的乘积，通过乘积精确判断一下I随R的变化是不是成反比关系.在计算出第一组IR乘积之后，准备下拉单元格操作之前，再凝聚注意力：I与R的乘积是不是一个不变的数值呢？稍作停顿，此时学生瞪大了眼睛，下拉单元格，完成5组I与R的乘积计算.数据如表3.

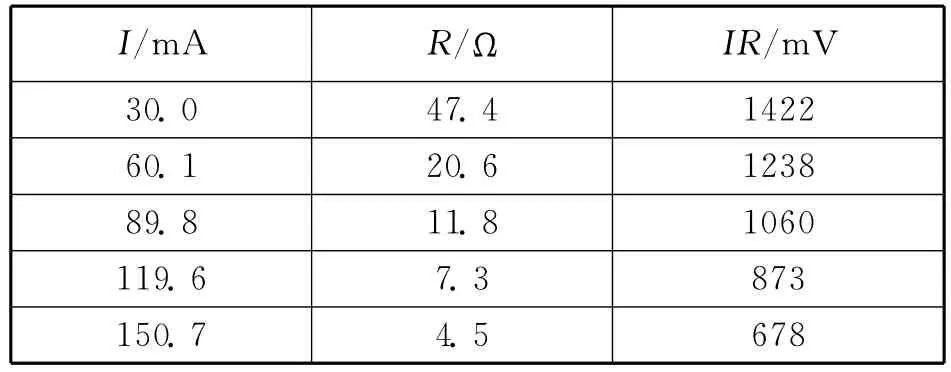
表3

师：I与R是否成反比？

生：不成反比.这回学生异口同声地回答.

师：怎么和刚才的预测不一样呢？

生：一时无言以对.

师：要想解释这个问题，需要考虑整个电路，学习闭合电路欧姆定律.

环节2.解释现象，提出猜想.

师：刚才的实验结果表明，I与R不成反比.I与R的定量关系不清晰了.学生们思考一下：电流I与R之间的定量关系可能是怎样的呢？大家可以讨论一下.

生：同桌、前后桌开始讨论.

师：汇报一下你们的想法，并说明理由.

生1：电流有可能与R、电源的内阻r之和成反比，因为电源有内阻，对电流也有阻碍作用.

生2：有可能，毕竟大致上还是R越大，电流越小.

生3：我发现电流变2倍的时候，电阻箱（接入阻值）减得比一半多

生4：要是知道电源内阻就好了，可以加上试试.

师：我也觉得电流有可能和电路中的总电阻成反比.学生4的想法倒是给了我们启发，验证我们的猜想是不是正确.关键是怎么找到电源的内阻呢，大家能不能从数据中再想想办法.

环节3.数据探究，验证假设.

生：经过5min左右的讨论，还是学生4提出想法：如果电流与总电阻成反比，它们的乘积应该是一个定值.所以如果假设电流与总电阻成反比，就存在一个关系式：I1（R1＋R）＝I2（R2＋R），就可以根据两组数据计算出R，这个R的意义就是除电阻箱以外其余部分的阻值.实验过程中，只是电阻箱的阻值发生了改变，R没变，所以我们可以把R加到每一次电阻箱的阻值上，得到每一次的总电阻值，这样就可以验证I是否与总电阻成反比了.

师：大家觉得学生4的想法是否可行呢？

生：有不少学生点头，还有的说：目前感觉没问题，要不现在试试吧.

师：那我们就任选两组数据计算一下R的值，找到电阻箱以外的那部分电阻.为了节约计算时间，我还给大家准备了计算器呢.

生：很快计算出了结果：R＝6.1Ω.是利用1、5组数据计算的.

师：好，这下总电阻也就找到了.我们用Excel计算一下电流与总电阻的乘积，验证一下学生4的想法.在计算出第1组I（R＋R′）乘积之后，准备下拉单元格操作之前，再凝聚注意力：I与（R＋R′）的乘积是不是一个不变的数值呢？稍作停顿，此时学生瞪大了眼睛，下拉单元格，完成5组I与（R＋R′）的乘积计算.数据如表4.

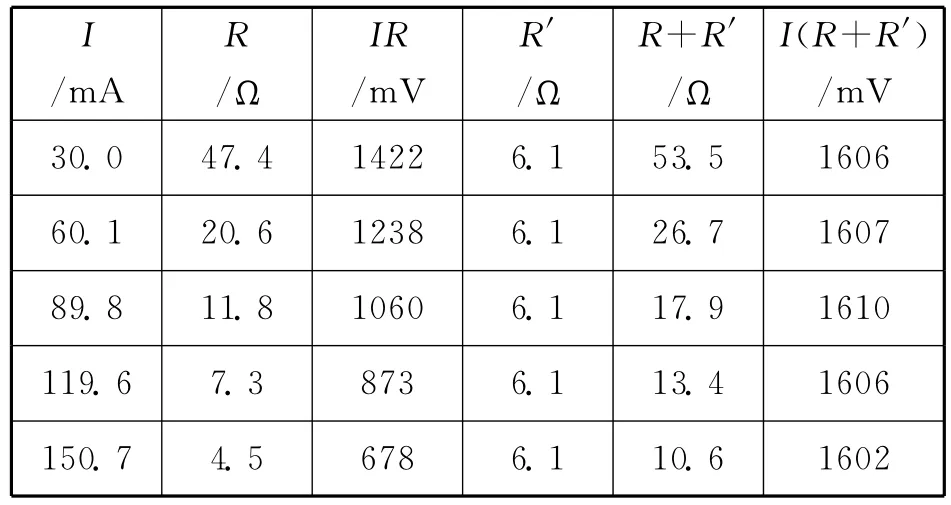
表4

生：目不转睛地盯着屏幕上的数据，当所有I（R＋R′）数据出来之后，I与总电阻（R＋R′）成反比的猜想得到了支持，欣喜之情溢于言表.

环节4.建立闭合电路欧姆定律，理解定律内容的物理意义.

师：从实验数据上看，I（R＋R′）乘积大小基本保持不变，支持了电流与总电阻成反比的猜想.请学生们再想一想I（R＋R′）乘积大小的物理意义是什么？是由谁来决定的呢？

生：不少学生回答I（R＋R′）乘积大小的物理意义为电路的总电压，是由电源决定的.

师：你们所说的“总电压”大小其实就等于我们之前学过的电源电动势大小.刚才的实验操作过程中我们没有改变电源，在实验的这段不长的时间内，电源电动势基本保持不变.那现在我们可否归纳一下电流I与R的定量关系式呢？

师：其实在1826年的时候，欧姆也像我们刚才一样做过类似的研究，我们看一看欧姆当年是怎样做的.播放自制的欧姆发现定律的视频.

生：观看视频，了解欧姆的工作，梳理本节课的探究过程.

师：点拨与总结：欧姆的温差电池作用相当于我们用的干电池，受当时科学技术水平的限制，欧姆只能用磁偏角间接测量电路中的电流强度，但是欧姆重复做的实验次数比我们多，还做了一些我们本节课没有来得及做的工作.经过大量的实验反复检验，的描述是令人满意的，欧姆的a相当于电动势，b相当于除待测导体以外其余部分的电阻，X相当于电流强度.

这是刚才实验的电路图（如图4），当开关闭合时，整个电路就构成电流的一个闭合通路，称为闭合电路.其中，电源外部的电路，称为外电路，电源内部的电路称为内电路，一个闭合电路就是由内电路和外电路组成.外电路两端的电压，我们称之为路端电压，就是图中A、B两点间的电压.

现在我们可以这样来表述闭合电路欧姆定律：闭合电路的电流跟电源的电动势成正比，跟内外电路的电阻值之和成反比.正如学生们刚刚总结出来的

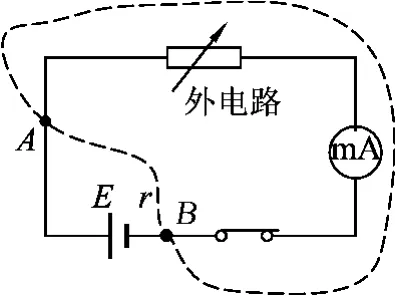
图4

环节5.小结.

组织学生回顾闭合电路欧姆定律的建立过程，梳理出所承载的科学研究方法：实验发现问题→提出假设→设计实验验证假设→归纳总结规律.引导学生反思引入过程认知冲突的原因，点拨部分电路欧姆定律的适用条件，强调闭合回路是一个系统，决定电流大小的因素是电源的电动势和内外电阻之和，路端电压是随着电路的变化而改变的物理量，使学生突破初中建立的简单电路模型，促进学生对电路认知的进一步发展.

4 结语

通过课堂观察，在本节课仿历史的实验和数据探究过程中，学生从思维层面深度参与，提出了很多有创造性的猜想和解决问题的思路、方法.在播放欧姆发现定律的历史视频时，学生表现出极大的兴趣，专心地观看，当发现自己所提出的猜想和解决问题的方法同欧姆当年很相似的时候，表现出非常激动和自豪的样子：自己也可以像物理学家一样思考.这恰恰是一个物理教师所期待的.

物理学的概念和规律，如果亲历了它们形成和发展的过程，会更加深刻地理解其含义；重新体验科学家研究问题的方法和思维过程，也使科学方法的传授不再是空洞的说教，而是有声有色的鲜活经历；物理学的发展史本身就是一部不断创新的历史，物理学前进的每一步都是创新教育的极好题材；而科学发现的不平坦之路又蕴含着多少深刻的人文价值.笔者期待，物理教育工作者认真思考和广泛关注物理学史在中学物理教学中的深度应用问题，创造出更多生动的教学案例来体现“真实的科学”、“历史的科学”，使学生感受真正的“科学文化”.

1 （美）弗卡约里著，戴念祖译，范岱年校.物理学史.桂林：广西师范大学出版社，2008.173－176

2 宋德生，李国栋著.电磁学发展史第2版.南宁：广西人民出版社.1996.171

3 郭奕玲，沈慧君著.物理学史第2版.北京：清华大学出版社，2005.107－109

4 贺艳军.物理学史融入西藏高中物理教学的现状研究——以重庆市北碚区为例（硕士论文）.西藏大学，2010.

5 李远俊.中学物理教学中引入物理学史的作用研究.重庆：西南师范大学物理系，2002.