一种改进的自适应线谱增强器＊

张春红

（中国船舶工业系统工程研究院 北京 100036）

1 线谱增强器原理

自适应线谱增强器通过对环境的自学习，对系统参数进行自调整，当信号频谱变化时，滤波器的频率响应能自动跟踪这种变化，从而达到对正弦信号线谱增强的目的［1～2］。

自适应FIR线谱增强器的原理框图如图1所示。图中，x（n）为输入数据，Δ为时延，wi（n）为自适应滤波器权系数（i＝1，2，…，L），L为权长，采用LMS算法。时延Δ 的作用是噪声解相关，x（n）通过Δ后，保持了信号的相关性。滤波器的输出y（n）为信号的最小均方估计，而输出e（n）为噪声的最小均方估计。复数LMS算法权系数迭代公式为［3～5］。

图1中e端为陷波器的输出端，y端为线谱增强器的输出。

图1 自适应LMS算法的FIR 线谱增强器结构

2 用自相干累加算法改进ALE的性能

采用LMS算法的横向滤波器结构的线谱增强器，由于存在着迭代噪声，因而其处理增益在输入信噪比很低时，ALE的性能很差。而且迭代噪声是随自适应权个数的增加而增大的，因而权个数不宜太多，故ALE 的增益受到限制。可以证明ALE的延时Δ和自适应滤波器等效于 整数倍的相移器，因而可以利用相干累加技术来改进ALE 的性能，原理框图如图2所示［6～8］。

图2 带有自相干累积器的ALE原理框图

图2中右边部分为相干累积器。相干累积器像是一个一阶递归滤波器，β为常数，通常取0＜β＜1 来保证系统的收敛性。其中延时Δ和横向滤波器W（k）是ALE的实时拷贝。对信号而言，它们是2π整数倍的相移器，因而在累加过程中，信号分量将同相相加，而干扰分量仅是能量相加。因此系统将取得显著的处理增益。本文将LMS算法的推广算法IGACI算法 应用于带有自相干累积器的ALE。

基本计算公式如下

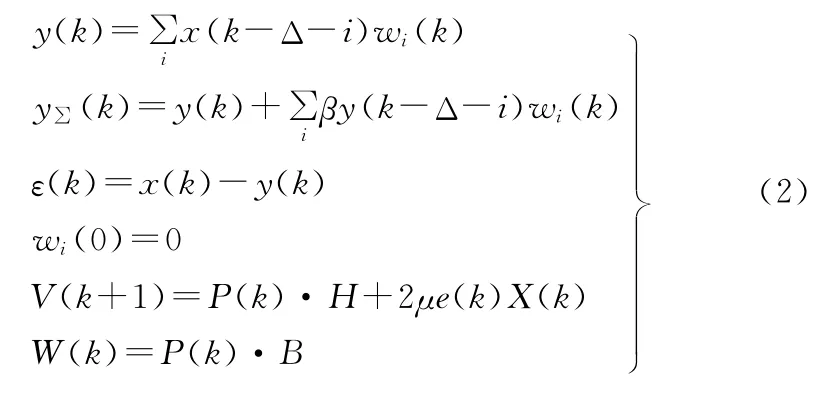
其中参量的定义参见文献［3］。

计算机仿真条件：线性调频信号加高斯白噪声。调频信号中心频率30kHz，脉宽2kHz，脉冲持续时间50ms。仿真结果如图3所示。

图3 普通ALE与带有一个相干累积器的ALE性能比较

仿真结果分析：在SNR＝-15dB 的情况下，当利用IGACI算法的普通ALE已经不能检测出信号时，而带有一个累积器的ALE仍可以稳定地检测出信号，从而证明了带有一个累积器的ALE在信号检测方面的优越性。

3 快速收敛自适应线谱增强器

在某些情况下，LMS算法的自适应收敛速度仍不能令人满意，于是出现了它的改进算法——快速收敛算法［9～10］，原理框图如图4所示。

图4 快速收敛自适应线谱增强器原理框图

本文将IGACI算法用于图4中，则也可以增加其自适应收敛速度。

计算公式如下

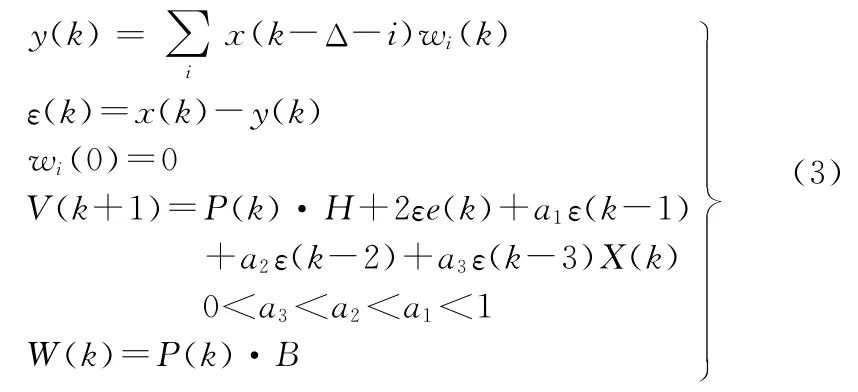
由于快速自适应线谱增强器不仅利用当前的误差信息，而且还利用前几次的误差信息，几个输出误差的线性组合大大消除了迭加噪声的影响，使误差信息更接近于真实值，通过对几个输出误差乘以不同的系数，使得越接近当前时刻的误差迭代时起的作用越大，因此它的搜索速度要比普通的ALE快得多。

计算机仿真：单频信号加高斯白噪声。一种情况是将IGACI算法用于普通的ALE，另一种情况是将IGACI算法用于快速收敛ALE。在快速收敛算法中取a1＝0.8，a2＝0.6，a3＝0.2。在相同的信噪比下选用相同的步长μ因子。图5和图6分别为两种算法误差函数的收敛曲线。

图5 快速IGACI算法的均方误差收敛曲线

图6 IGACI算法的均方误差收敛曲线

仿真结果分析：快速收敛算法的确收敛较快，但并没有得到很大的提高，分析原因可能是：1）利用误差函数的历史信息可能还较少，增加ai的个数应该还可以进一步提高算法的收敛速度；2）IGACI算法已经利用了较多的历史信息，因此收敛速度已经比较快，再加入误差函数的历史信息，也不会得到大幅度的提高。但我们这样的探讨还是有意义的。

4 结语

本文主要讨论一种现在使用最广的自适应滤波器—自适应线谱增强器（简称ALE），并进一步介绍了ALE 的两种改进形式—带有自相干累积器的ALE 和快速收敛ALE。将IGACI算法用于带有自相干累积器的ALE 和快速收敛ALE，分别提高了ALE 在低信噪比下的检测性能和收敛速度。

［1］N.Ahmedand S.Vijayendra.An Algorithm for Line Enhancement［J］.Proc.IEEE.1982，70：1459-1460.

［2］王彦，马章勇，黄建人.一种用两个相干累积器提高自适应谱线增强器性能的方法［J］.声学技术，2003，22（1）：8-10.

［3］王蓬，梁红，李志舜.广义的自适应相干累积算法［J］.西北工业大学学报，2005（1）：107-109.

［4］Neil J.Bershad，Francis A.Reed.Tracking Characteristics of the LMS Adaptive Line Enhancer-Response to a Linear Chirp Signal in Noise［J］.IEEE Transactions On Acoustics，Speech，And Signal Processig，1980，28（5）：504-516.

［5］Treichler J R.Response of the adaptive Line Enhancer to Chirped and Doppler-Shifted Sinusoids［J］.IEEE Trans Acoustics，Speech，Signal Processing，1980，ASSP-28（3）：343-348.

［6］C.C.Ko，C.P.Li.An adaptive IIR structure for the separation，enhancement，and tracking of multiple sinusoids［J］.Signal Processing.IEEE Transactions on.1994，42（10）：2832-2834.

［7］T.Kwan，K.Martin.Adaptive detection and enhancement of multiple sinusoids using a cascade IIR filter［J］.Circuits and Systems.IEEE Transactions on，1989，36（7）：937-947.

［8］Nam Ik Cho，Chong-Ho Choi，Sang Uk Lee.Adaptive line enhancement by using an IIR lattice notch filter［J］.Acoustics，Speech and Signal Processing，IEEE Trans-actions on.1989，37（4）：585-589.

［9］P.A.Regalia.An improved lattice-based adaptive IIR notch filter［J］.Signal Proces-sing，IEEE Transactions on.1991，39（9）：2124-2128.

［10］ROBERT J.MCAULAY，Gradient Method for Systems with Time Delays and Its Application to Waveform Design.IEEE Transations On Automatic Contril，1996，14（3）：230-237.