船用柴油机喷油系统的退化可靠性评估＊

王 磊 林瑞霖 刘伯运

（海军工程大学动力工程学院 武汉 430033）

1 引言

应用传统方法对船用柴油机零部件进行可靠性评估往往有很大局限性，这是因为：一方面柴油机发生故障的时间具有很大的随机性，平时对其故障时间的记录工作比较繁琐，从而造成了试验数据的缺乏或不准，这对基于失效时间数据来进行计算的传统可靠性评估模型而言影响较大；另一方面，传统的可靠性评估模型很难与所测样品个体的当前状态相结合，缺乏针对性与实效性。本文在收集柴油机零部件外部可测的参数数据的基础上，通过建立基于性能退化数据的可靠性模型，并与性能故障判据关联起来，能避免上述问题，是一种评估柴油机零部件可靠性的有效方法。统计资料表明，柴油机喷油系统故障占其故障总数的27%［1］，因此，本文选取柴油机喷油系统作为研究对象，对其进行可靠性评估。

2 退化可靠性评估的基本方法

柴油机喷油系统的工作过程实际上可以看作是一个随着时间的延长，性能不断劣化，直至无法工作的退化过程。若对喷油系统的输出参数进行跟踪监测并评价其可靠性，首先需要构建其可靠性退化模型。在工程技术领域早已出现了很多涉及退化数据的实际问题，很多工程技术人员和统计学者，如Lu＆Meeker［2］，Crk［3］，庄东辰［4］等在对产品的性能退化数据进行可靠性分析的基础上，给出了基于性能退化数据的可靠性分析的基本方法与步骤：

1）收集所有样品在t1，t2，…，tm时刻的性能退化数据。

2）根据记录的性能退化数据估计各个样本性能退化模型的参数。假设第i个样品在时刻tj观察到的退化值为：yi，j＝D（ti，j，β1i，β2i，…，βki）＋εi，j，（i＝1，2，…，n；j＝1，2，…，m），这里D（ti，j，β1i，β2i，…，βki）为第i个样品在时刻tj的实际轨迹，εi，j为测量误差，一般情况下εi，j～N（0，σ2ε）。

3）估计出参数β1i，β2i，…，βki，即得到对象的退化模型。

4）获得每个参数与时间的拟合函数后，可得到任何时刻的性能退化数据的概率分布，即可基于指定的退化临界值进行可靠性推断。

3 喷油系统性能退化数据的收集

柴油机喷油系统经常出现的故障有喷油器开启压力降低、喷油孔堵塞、喷油器针阀偶件磨损等［5］。以前，检测喷射系统工作状况，一般采用的方法是用一个三通接头将压力传感器接入高压油管中来检测分析油管里的压力波，从而达到诊断故障的目的。这种检测方法必然要对原机油管进行拆卸和改动，不但会影响原燃油系统的结构和正常工作，还会给测量带来误差，而且作为现场检测也极不方便。为此，本文采用另一种方法，即采用夹持式传感器夹在高压油管上，不需对柴油机进行拆卸的情况下，通过测量分析高压油管膨胀波信号，即可判别燃油系统的工作状态，从而达到收集退化数据的目的。

通过对测试系统的数据分析可以发现，波形中最大压力、平均压力等参数可以反映出柱塞磨损的程度以及体现出喷油器不同的故障。文献［6］得出喷油系统状态表征的最佳参数是

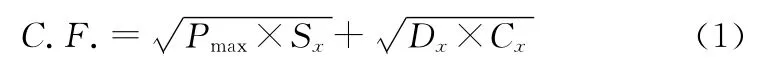
其中：C.F.代表复合特征量；Pmax表示最大喷油压力；Sx表示偏斜度，即三次原点距；Dx表示二次原点距；Cx表征峭度，即第四阶原点矩。该复合特征量能够能直接测得，它反映出喷油系统状态的变化，且具有可靠性的表征，因此可以利用这个复合特征量的变化构建柴油机喷油系统可靠性模型［7］。

以船用6135型柴油发电机组作为实验对象，收集柴油机上的喷油器高压油管测试实验历史数据并进行分析，得到高压油管压力的复合特征量C.F.的数据如表1所示。

表1 高压油管压力的复合特征量试验数据

4 喷油系统的退化模型

由于喷油系统的符合特征量是受诸多因素影响的，其退化的机理不明确，用物理或化学过程对其进行描述非常困难。实际上，可以把喷油系统的每次喷油看成对喷油组件造成的一次冲击，喷油系统的性能退化正是这种冲击带来的损伤的积累。而每一次冲击，由于应力水平和其他环境因素的不确定性，对喷油组件的损伤都有随机性。因此，采用随机过程模型来对它进行描述是一种有效的途径。

1969年Gertsbakh与Kordonskiy［8］在研究材料磨损时第一次提出了随机过程模型。该模型假设退化量与积累损伤有关，而损伤事件独立发生，每次冲击造成的损伤量是一个恒定的常量。

假设喷油系统的退化过程具有如下特点：

1）喷油组件的复合特征量在t时刻的退化量是相互独立的同大小的基本退化量Yi的积累；

2）基本退化量Yi的产生是随机的；

3）在一个给定的时间内可能产生的退化量与之前积累所产生的退化量是相互独立的。

则喷油系统复合特征量的退化过程满足一个非齐次泊松过程［9］，它的退化模型可用以下的积累损伤冲击模型［10］来描述：

其中，W（t）代表运行到t时刻复合特征量总的退化量；Yi表示每一次冲击所造成的退化量；N（t）表示冲击次数。

根据工程经验，并为了表示方便，冲击次数N（t）的强度函数λ（t）可以用一个幂律模型［11］来表示

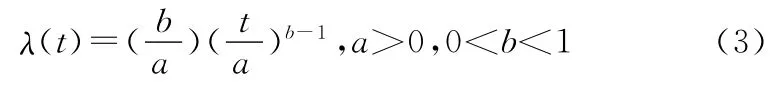
这样，得到冲击次数N（t）的均值函数M（t）为

根据模型假设，将Yi看作是一个未知的确定大小的常数c，则式（1）又可以表示为

这个冲击模型的期望和方差［12］分别为

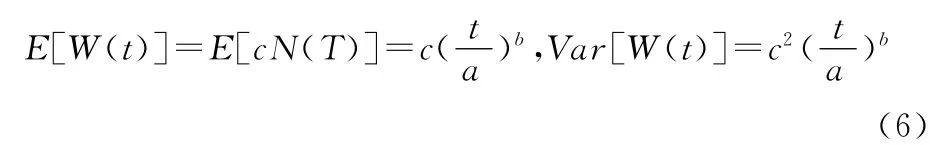
由非齐次泊松方程的性质，在时间（t1，t2）间的退化量w（t1，t2）为

其中N（t1，t2）表示在时间间隔（t1，t2）内的冲击次数，w＝0，c，2c，…。

设复合特征量的失效阈值为Wmax，当W（t）超过这个阈值时喷油系统失效，所以复合特征量的可靠度为

其中

5 参数估计

在式（3）表示的强度函数中，a和b都不确定，基本的退化量c也未知，无法用极大似然估计（MLE）来直接得出上述参数的估计值。因此可以用一种经过变换后的极大似然估计法来估计a，b，c的值。

1）估计＾b

结合式（4）与式（7），得到（a，b，c）的对数似然函数并求偏导得

其中，Δwi，j＝wi，j-wi，j-1表示在时间（ti，j-1，ti，j）内的复合特征量的退化量；m表示样本个数；ni是第i个样本总的试验次数。Wi，ni表示第i个样本运行中总的退化量。

可见θ只有b一个变量。

将式（11）代入式（10），对b求偏导并令其为0得

根据式（13），可求得b的估计值。

2）估计

由式（6）和式（11），对于Δwi，j，有

设有一随机变量yi，j，即

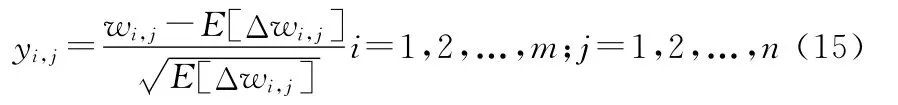
从式（15）可以看出yi，j的均值为0，结合式（14）可知yi，j方差即为c。

3）估计

由式（12），有

利用Matlab对式（13）进行编程，其中运用二分法［13］接近（如图1所示）。最后解得＝1.1128＝0.0831＝0.0089＝7.4450。得到喷油系统复合特征量退化量的计算公式为

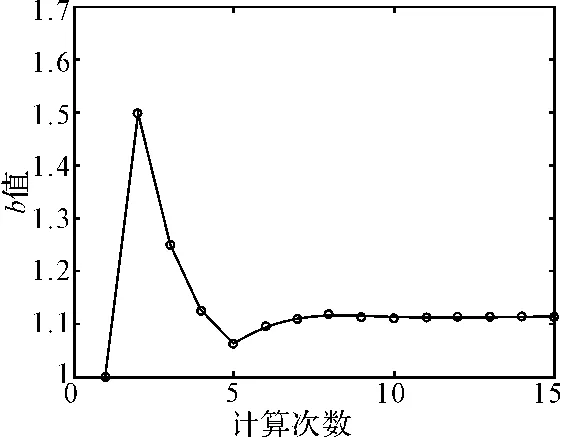
图1 二分法计算b值

拟合曲线如图2中实线所示。

图2 拟合曲线

若设喷油系统的失效阈值Wmax分别为5、10、15，则求得Kmax分别为61、121、181，根据式（8），得到喷油系统的可靠度曲线分别如图3所示。

图3 喷油系统可靠性曲线

6 结合Bayes方法的改进

由上一节的分析结果可以看出，可靠性曲线受参数c，即基本退化量的影响较大。c的精确度取决于样本的大小。在小子样条件下，如果运用上述得到的先验分布（π）θ结合Bayes方法改进上述过程，则能得到更精确的结果。

根据Bayes公式［14］可得未知参数的联合后验分布函数为

其中，Ξ、Θ、Λ 分别表示a、b、c的取值范围。由式（17）可得到a、b、c的后验分布

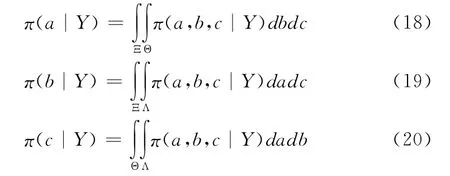
由式（18）、（19）、（20）所示的关于a、b、c的后验分布出发进行分析，即可得到关于a、b、c的后验估计，使得到的结果更为精确。

7 结语

本文运用非其次泊松的退化模型对船用柴油机的喷油系统进行了可靠性研究，并提出了在小子样条件下，运用Bayes定理进行改进的方法。由于设备的复合特征参量物理含义明确，且易于测量，因而该方法实用性强，克服了传统可靠性建模需要大量可靠性试验数据的缺点。本文对柴油机喷油系统退化过程所建立的可靠性退化模型对于其柴油机其他零部件的可靠性建模具有参考价值。如果在本方法的基础上，建立起柴油机整机系统的可靠性退化模型，则对柴油机的视情维修、寿命预测分析，具有重要意义。

［1］吴兆汉，蔡坪，陈深龙.内燃机可靠性设计［M］.北京：北京理工大学出版社，1988：290-291.

［2］C J Lu，W Q Meeker，Using Degradation Measures to Estimate A Time-to-Failure Distribution［J］.Techno-Metrics，1993，35（2）：161-174.

［3］Crk V.Reliability Assessment From Degradation Data［C］.Proceedings Annual Reliability and Maintainability Symposium，2000：155-161.

［4］庄东辰.退化失效模型及其统计分析［D］.上海：华东师范大学，1994.

［5］乔新勇，刘利东，康葳，等.基于压力波的柴油器喷油器故障诊断研究［J］.无损检测2004，26（4）：180-198.

［6］屈梁生，吴松涛.统计模拟在工程诊断中的一些应用［J］.振动、测试与诊断2001，21（3）：157-167.

［7］周正伐.可靠性工程基础［M］.北京：中国宇航出版社，2010：48-53.

［8］汪荣鑫.随机过程［M］.西安：西安交通大学出版社，2006：211-214.

［9］Gertsbakh I B，Kordonskiy K B.Models of Failure［M］.Springer-Verlag，1969：112-123.

［10］刘德华.泊松冲击下退化失效模型的统计分析［D］.华东师范大学，2009：1-2.

［11］曹晋华，程 侃.可靠性数学引论［M］.北京：高等教育出版社，2005：432-438.

［12］庄楚强，何春雄.应用数理统计基础［M］.广州：华南理工大学出版社：2005.15-17.

［13］王沫然.MATLAB与科学计算［M］.北京：电子工业出版社，2004：382-389.

［14］Berger O.Statistical Decision Theory and Bayesian Analysis（Second Edition）［M］.New York：Springer Verlag，2004：78-90.