直线感应电机次级结构对电磁力影响仿真分析＊

谢保状 王铁军 李 兵

（海军工程大学 武汉 430033）

1 引言

直线感应电机成功地用于驱动轨道交通中的磁悬浮列车和地铁车辆等［1］。它因为可以将电能直接转换成直线运动机械能，而不需通过任何中间转换机构而备受青睐。

目前直线电机建模方面均比较困难，非参数建模的方式较多［2］。直线电机在结构上难以做到三相对称，会出现端部效应，端部效应将同时影响到对直线电机的法向力、电磁推力和其它特性的准确分析［3］。

本文对比较常用的低速扁平单边型直线感应电机展开分析，运用Ansoft电磁场仿真软件，对改变电机的次级导电部分结构对初级受电磁力进行分析，定性作出这些参数对电机电磁力影响的结论。

2 低速扁平单边型直线感应电机的基本原理

扁平型直线感应电动机是应用最广泛的一种直线感应电动机，其次级可以是铝、铜、铁或复合的［5］。次级影响直线电机性能的主要因素在其材料的导电和导磁性能上。复合次级通常由导电部分（铜板或铝板）和导磁部分（实心或叠片的铁轭）组成。对次级固定，初级运动的短初级长次级直接感应电动机而言，初级受与行波磁场同向的电磁推力和与其垂直的法向力。对初级绕组通入对称三相交流电后，会产生平移的行波磁场，次级导电部分在行波磁场切割下，将感应电动势并产生电流，并和行波磁场相互作用对初级产生电磁推力。次级导电部分感应出涡流，导磁部分起到形成闭合磁路作用［5～10］。

等效电路法对直线感应电机的分析和综合都是有效的，电机的性能可以很容易从计入边缘效应的等效电路中得出［2］。图1为考虑纵向边缘效应的等效电路图。有效推力

式中，m1为相数；ke为纵向边缘系数；z′2为定子侧绕组阻抗；E1为动子侧绕组绕组感应电动势；R′2为定子侧（履带）绕绕组电阻折算值；S为动子运动的滑差率；vs为同步速度；ΔFm为机械损耗对应的力。

图1 考虑纵向边缘效应的等效电路图

法向力Fz由两部分组成，即引力Fza和斥力Fzr，法向力由两部分组成，一是初级与次级导磁部分的吸引力，其值成正比于气隙磁密的平方；另一个是次级导电部分的涡流对初级的排斥力作用，其值成正比于涡流平方的大小，法向力由二力合成。即Fz＝Fza-Fzr。

3 直线感应电机次级结构对电磁力影响的仿真分析

推力是直线感应电动机一项重要的技术指标，直线感应电动机的推力-速度特性近似成一条直线，最大推力在高转差处，即转差率S＝1附近，因此，往往只验证启动时的推力值［3］。磁通能透入次级导体内部的深度称为渗透深度，当采用的次级材料的厚度大于其在当前工作频率的渗透深度时，集肤效应的影响就变得显著，再加大次级厚度对电磁性能影响很小［4］。

小于50Hz时，铁板渗透深度大概为2mm。而对于铝或者铜等非磁性材料，其渗透深度在10mm 以上。为分析次级导电部分厚度、与初级间距大小对电磁力影响，利用Ansoft软件建模，扁平型单边直线感应电动机二维仿真模型侧视图如图2，极距96mm，绕组匝数150匝，通10Hz、最大值为10A 的三相对称交流电，星形连接如图3，两套绕组采用顺串连接。铜板做次级导电部分，铁板做次级导磁部分，铁板厚10mm，设定铁的渗透深度为2mm。

图2 二维仿真模型侧视图

图3 直线电机绕组连接示意图

图4 二维模型主视图

选定初级、铜、铁为受力分析对象，三者均固定，即转差率S＝1，初级距铁板的气隙L为6mm，设定铜板距初级h＝3mm，铜板厚度d＝1mm，如图4所示，分析步长step＝0.0001s，分析时间0s～0.25s。受推力与法向力如图5、图6，可见，初级受推力主要由行波磁场与铜板相互作用产生，法向力主要由初级与铁板相互作用产生。

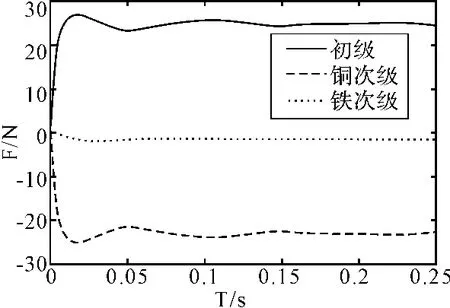
图5 受推力-时间曲线

图6 法向力-时间曲线

1）铜板距初级距离对直线感应电机电磁力影响分析

为分析铜板距初级距离对直线感应电机电磁力影响，固定所有参数，设定铜板厚度d＝1mm，改变铜板与初级位置h，建立四个模型进行分析，得仿真结果图7、图8。

图7 铜板不同位置时初级受推力-时间曲线

图8 铜板不同位置时初级受吸附力-时间曲线

以上仿真结果表明，气隙及铜板厚度不变时，改变铜板位置，对推力与吸附力影响均不大。铜板距初级近时，初级受电磁推力稍大一些。

2）铜板厚度对直线感应电机电磁力影响分析

为分析铜板厚度对直线感应电机电磁力影响，固定所有参数，铜板距初级h＝3mm，改变铜板厚度d，建立六个模型，得仿真结果图9、图10。

图9 铜板不同厚度时初级受推力-时间曲线

图10 铜板不同厚度时初级受吸附力-时间曲线

以上仿真结果表明，在气隙及铜板与初级距离不变时，当其厚度小于渗透深度，加大铜板厚度，对初级受推力增加明显；在低频低速时，铜板厚度对初级受吸附力影响不明显，铜板越厚，吸附力越小。

3）铜板更换为与初级等宽、两端导通的铜条，铜条与铜条间隔相等时，不同宽度对直线感应电机受力影响分析

建立三维模型如图11，扁平型单边直线感应电动机，参数均不变，初级距铁板的气隙L为6mm，铜板2mm 厚，距初级3mm。改变铜板结构如图12，其效果等同于将铜板更换为宽度为n、两铜条间隔m的矩形铜条，铜条两端导电。

图11 三维仿真模型斜视图

图12 铜板俯视图

当m＝n时，建立三个模型，得仿真结果如图13、图14。根据图13、图14仿真可以看出，m与n大小相同即铜条和间隙等长时，初级受推力均值近似恒定，其值越大，受力随时间变化的波动越剧烈；结构改变对初级受吸附力影响不大。

图13 m 与n 相等时初级受推力-时间曲线

图14 m 与n 相等时初级受吸附力-时间曲线

4）铜条与铜条间隔比例不同时对直线感应电机受力影响分析

恒定铜条间隔m为1mm，改变铜条宽度n，另分析三维模型里铜板和无铜板的受力情况，得仿真结果如图15、图16。

图15 m 与n 不等时初级受推力-时间曲线

图16 m 与n 不等时初级受推力-时间曲线

从仿真可以直观看出，m／（m＋n）的值越小，推力越大，即两端导电的铜条取代铜板作为直线电机次级导电部分时，更小的间隙才可能产生更大的推进力；结构改变对初级受吸附力影响不大。

4 结语

本文分析了影响直线感应电机重要部分——次级导电部分，从电磁场仿真的角度出发，建立多个模型，仿真结果直观的给出了次级导电部分结构对电机的电磁力影响。次级导电部分的厚度对推力影响明显，与初级距离对初级受推力影响不明显。当次级导电部分被与初级等宽、两端导通的铜条取代时，单根铜条面积越大，两根铜条间隙越小，产生推力越大而平稳。该结论为直线感应电机的应用和设计提供了参考，为后续研究奠定基础。

［1］吕刚，范瑜，李国国，等.基于解耦策略的直线感应牵引电机法向力自适应最优控制［J］.中国电机工程学报，2009，29（9）：78-85.

［2］吕刚，范瑜，马双云.直线感应电机推力和法向力的解析计算与分析［J］.电机与控制学报，2010：77-82.

［3］叶云岳.直线电机原理与应用［M］.北京：机械工业出版社，2000：46-48.

［4］赵博，张洪亮.Ansoft 12在工程电磁场中的应用［M］.北京：中国水利水电出版社，2010：174-189..

［5］S.A.Nasar，I.Boldea.Linear Motion Electric Machines［M］.北京：科学出版社，1982：55-65.

［6］Idir K，Dawson G E，Eastham A R.Modeling and performance of linear Induction motor with saturable primary［J］.IEEE Transactionson Industry Applications，1993，29（6）：1123-1128.

［7］龙遐令.直线感应电动机的理论和电磁设计方法［M］.北京：科学出版社，2006：125-134.

［8］Nasar S A，Boldea I.Linear motion electric machine［M］.New York：Wiley，1976：30-50.

［9］Jacek F.Gieras.“Linear Induction Drives”［M］.Clarendon press，Oxford，1994.

［10］Ion Boldea，Nasar S A.Linear motion electromagnetic devices［M］.New York：Taylor＆Francis，2001：15-20.