火炮身管等效全装药寿命换算方法研究

徐东升，刘广生，贾长治，陶辰立

(军械工程学院 火炮工程系，河北 石家庄 050003)

身管寿命基本决定了整门火炮的寿命，准确的预测判断身管寿命对于火炮的设计、使用和维修都有着重大的意义[1-2]。火炮发射装药号是影响身管寿命的重要因素之一，因此对于变装药的大口径地面火炮而言，在利用射弹量判断身管寿命时，必须将不同装药条件下的射弹发数等效成标准装药条件下的射弹发数[3]。

尽管目前国内外在进行火炮初速修正的时候，提出了对不同装药量进行等效的当量射弹发数法。

但是实践表明，由于各种非标准射击条件下和标准条件下的身管内膛径向磨损速率之比难以确定[4]，而且不同火炮的发射药成分和内膛结构不同，该方法很难达到实际应用的程度。

针对这一问题，本文提出了一种火炮身管等效全装药寿命换算方法，该方法以膛线起始点的总热量和膛内总压力冲量为中间变量，通过计算不同装药号与全装药之间的等效换算系数，确定火炮身管的等效全装药寿命。

1 身管等效全装药寿命换算方法分析

内弹道研究表明，身管寿命的不断下降实际上是由烧蚀和磨损两个方面决定的，烧蚀是指火炮射击时，火药燃烧以及弹丸的高速运动使得身管内膛处在反复的冷热循环状态和物理化学作用下，引起内膛金属材料性质的改变；磨损则是指由于弹丸的弹带、弹体对膛线的机械磨损作用或者是高压条件下的气流冲刷作用引起的身管的几何形状的改变[5-6]。

身管寿命的下降既然是由于烧蚀磨损导致的，而烧蚀则主要是在高温情况下才能进行，同样磨损也主要是由于高膛压推动弹丸挤进以及使得火药气体、未燃烧完成的火药颗粒的高速运动引起的，即使是火炮射击时，内膛的化学反应也是在不同的温度情况下存在不同的反应生成物。因此，火炮身管寿命的下降就可以归结为内膛高温和高压的共同作用结果，在进行身管寿命预测时，也就可以将内膛的温度和膛压作为中间变量进行等效换算。

能够反映内膛温度的特征量有膛内最高温度和膛内不同位置的输入总热量两个。研究表明，对于同一种发射药而言，由于爆温相同，膛内最高温度基本相同，无法反映射击条件变化对身管寿命的影响，同时由于火炮射击时内膛环境恶劣(高温、高压、高速磨损)，内膛温度的准确测量是十分困难的。而膛内不同位置的输入总热量不仅能够反映各种不同射击条件下的身管烧蚀，而且可以采用内弹道计算获得。因此，对于膛内温度这一中间变量而言，本文采用膛内的输入总热量作为等效换算的中间变量。依据这一分析，根据经典内弹道理论，膛内输入总热量由内弹道变容状态方程决定[7]：

(1)

式中，S为炮膛断面积;p为压力;lψ为药室自由容积缩径长;l0为药室容积缩径长;ω为装药质量;φ为火药已燃百分数;R为气体常数;T为燃气温度;Δ为装填密度;α为火药气体余容。

对于膛内输入总热量这一特征量，身管内轴向不同位置的值是不同的。由于一般情况下，膛线起始点身管内膛烧蚀磨损最为严重，也最能反映身管的寿命，因此，最终采用膛线起始点的输入总热量作为中间变量，计算由膛内温度确定的不同装药条件下的身管等效寿命换算系数。

同样，能够反映膛压的特征量有最大膛压和膛内输入总压力冲量两个。而从身管寿命下降的角度来说，最大膛压反映了火炮的弹道性能，但是火炮射击时弹丸的高速运动以及火药气体的冲刷、未燃烧完成的火药颗粒的高速运动对于身管的磨损，是由于膛内压力不断作用的结果，因此，从身管寿命下降的根本原因出发，以膛内输入的总压力冲量作为等效换算的中间变量更为合理。膛内输入总压力冲量同样可以依据经典内弹道理论，利用一般的n种火药混合装药内弹道数学模型[7]计算：

(2)

其中，

当应用多孔火药时，ψi方程就改写为计及分裂点的形状函数：

对公式(2)进行编程计算获得膛压变化曲线，积分后即为膛内输入总压力冲量，对比不同装药条件下的膛内输入总压力冲量，可以计算由膛内压力确定的不同装药条件下的身管等效寿命换算系数。

由于影响火炮身管寿命的主要射弹条件是装药号、药温、射击频率以及弹种，因此，利用该等效方法，只需要分别计算不同射弹条件下的膛内输入总热量和输入总压力冲量换算系数，并综合两个换算因素对身管寿命的影响，就可以确定不同射弹条件下的等效身管寿命射弹发数。如图1所示，是利用该方法进行身管寿命等效换算的思路。

2 算 例

以某型大口径火炮为例，依据本文提出的身管等效全装药寿命换算方法，计算其强装药和减装药射击条件下相对于全装药的等效换算系数。

根据变容状态方程，计算获得该火炮在15℃药温、4发/分钟的射击条件下，全装药和减装药的膛线起始点内温度变化曲线如图2和图3所示。

分别对全装药和减装药条件下的温度进行积分求和，获得不同装药下膛线起始点的输入总热量。此时，当取全装药条件下的系数为1.0，减装药条件下的等效换算系数为0.882。同样，利用一般的n种火药混合装药内弹道数学模型，计算获得同种火炮在15℃药温、4发/分钟的射击条件下，使用全装药和减装药时膛压随时间变化曲线，如图4和图5所示。

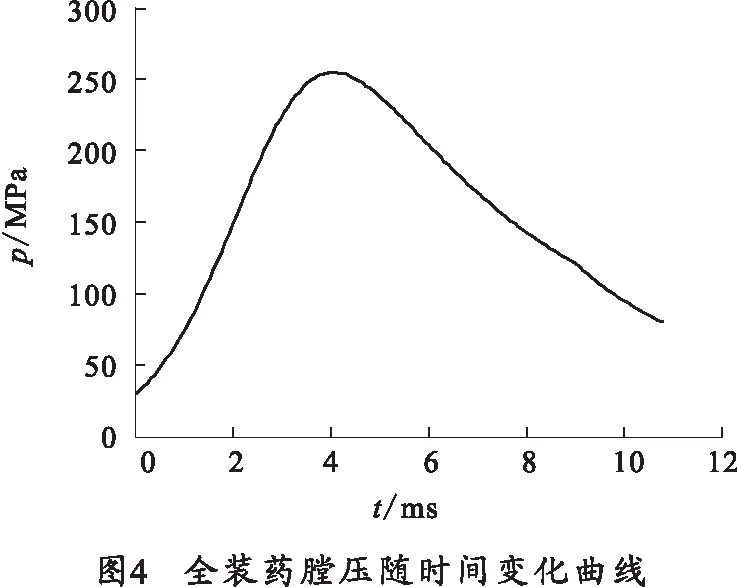
分别对全装药和减装药条件下的膛压进行积分求和，获得不同装药下膛线起始点的输入总压力。此时，当取全装药条件下的系数为1.0，减装药条件下的等效换算系数为0.455。

因此，综合温度影响系数和压力影响系数，对不同的换算系数求积，获得该种火炮在15°C药温、4发/分钟的射击条件下，减装药和全装药的等效寿命换算系数0.4。

文献中，利用单因变量回归模型，采用最小二乘法计算了全装药和减装药的等效寿命换算系数，其结果为0.395，对比本文算例中的结果，基本是一致的。因此，本文提出的身管等效全装药寿命换方法是比较合理的，可以利用该方法对身管的等效装药射弹发数进行计算。

3 应 用

利用该方法，本文对某型大口径火炮在不同装药射击条件下的等效寿命换算系数进行了计算，该火炮在正常射击情况下采用0～6号共7个装药号，其中0号装药表示全装药，取其系数为1.0，其他装药号的温度等效换算系数、压力等效换算系数以及最终身管等效寿命换算系数计算结果分别如表1～表3所示。

表1 身管等效全装药寿命温度换算系数

表2 身管等效全装药寿命压力换算系数

表3 身管等效全装药寿命换算系数

因此，利用表3中的结果，当进行该型火炮身管寿命判断时，在不同的装药条件下的射弹量只需乘以表中的换算系数，就可以获得当量射弹发数。例如，对于6号装药，其换算系数为0.272，那么射击1发6号装药炮弹的身管寿命下降量就为当量全装药0.272发。

4 结 论

本文通过分析火炮身管烧蚀磨损寿命下降的实质，提出了一种火炮身管等效全装药寿命换算方法，利用该方法计算了某型火炮全装药和减装药射击条件下的身管寿命等效换算系数，并通过与单因变量回归模型的计算结果进行比较，验证了本文提出的计算方法是合理的。

在此基础上，本文对某型火炮正常射击条件下采用的不同装药号进行了身管等效全装药寿命换算系数的计算，该系数可以应用于火炮射击时表征身管寿命的射弹量的当量换算。

[1] 高付申，邱文坚，梁世超，等．火炮身管寿命预测问题的研究[J]．南京理工大学学报，1997，21(3)：229-232.

GAO Fu-shen, QIU Wen-jian, LIANG Shi-chao, et al. Study on the gun tube life prediction[J]. Journal of Nanjing University of Science and Technology, 1997, 21(3): 229-232. ( in Chinese )

[2] 李明涛，崔万善，姚哲，等．基于内表面熔化层理论的身管寿命预测方法[J]．火炮发射与控制学报，2009(2)：5-8.

LI Ming-tao, CUI Wan-shan, YAO Zhe, et al. Prediction method of barrel life based on inner side melting theory[J]. Journal of Gun Launch & Control, 2009(2): 5-8. ( in Chinese )

[3] 崔军，杜建革，穆歌．弹丸初速评定身管寿命研究[J]．火炮发射与控制学报，2003(增刊):134-137.

CUI Jun, DU Jian-ge, MU Ge. Study on assessment of cannon barrel Life by muzzle velocity of pill[J]. Journal of Gun Launch & Control, 2003 ( supplement ): 134-137 ( in Chinese )

[4] 张喜发，卢兴华．火炮烧蚀内弹道学[M]．北京：国防工业出版社，2001.

ZHANG Xi-fa, LU Xing-hua. Interior ballistics of erosion guns[M]. Beijing: National Defense Industry Press, 2001. ( in Chinese )

[5] 张振山，吴永峰．炮管内膛烧蚀磨损现象的分析[J]．装甲兵工程学院学报，2003，17(2)：67-70.

ZHANG Zhen-shan, WU Yong-feng. The analysis of the rubbing abrasion and erosion on the barrel bore[J]. Journal of Armored Force Engineering Institute, 2003, 17(2): 67-70. ( in Chinese )

[6] 张培忠，冯金富．火炮试验新技术[M]．北京：兵器工业出版社，2005.

ZHANG Pei-zhong, FENG Jin-fu. New technology of gun test[M]. Beijing: The Publishing House of Ordnance Industry, 2005. ( in Chinese )

[7] 金志明．枪炮内弹道学[M]．北京：北京理工大学出版社，2004.

JING Zhi-ming. Gun Interior ballistics[M].Beijing: Beijing Institute of Technology Press, 2004. ( in Chinese)