信息熵和主观偏好综合的空袭目标威胁评估

王 越，赵 凯，翟二宁，张 堃

(1.西北机电工程研究所 陕西 咸阳 712099，2.西北工业大学，陕西 西安 710129)

空袭目标威胁评估是防空武器系统指挥作战的重要一环，是我方防空火力分配和指挥决策的前提和基础。空袭目标威胁评估本质上是多指标决策问题。指标权重赋值是解决多指标决策问题的关键，权重赋值的方法主要有主观赋权法和客观赋权法。主观赋权法是根据决策者主观偏好信息直接或间接给出指标权重。如层次分析法[1]、灰色聚类分析法[2-3]等。客观赋权法是通过求解根据目标的各项指标值所建立的数学模型反推计算出的指标权重。如信息熵权法[4]、最小加权隶属度法[5]、topsis[6]法等。主观赋权法依赖于专家的经验和偏好, 有一定的盲目性。客观赋权法能够充分利用战场态势信息，但完全忽视主观偏好, 有时会出现权重不合理的现象。

本文采用区间数表示不同传感器的测量值和定性指标等不确定信息。利用信息熵理论求得指标客观权重，再与专家给出的主观权重相乘归一化获取综合指标权重。运用模糊决策理论建立各目标相对于正理想目标的关联系数的数学模型，通过比较关联系数确定目标威胁度排序。

1 空袭目标威胁评估指标

空袭目标威胁评估是多指标决策问题，令X={x1,x2,…,xn}为空袭目标方案集，U={u1,u2,…,um}为评估指标集。目标xi按评估指标uj进行测度，记为aij，于是可得目标威胁决策矩阵A={aij}n×m。根据防空武器系统的特点和空袭目标的飞行特性，选取6个因素组成威胁评估指标集：U={目标类型，飞临时间，飞行速度，航路捷径，飞行高度,干扰能力}。

2 目标威胁评估指标权重的获取

区间数是一类特殊的模糊数，为描述不确定性提供了一种有效途径，目标威胁评估指标既有定量指标又有定性指标，有很大的模糊不确定性，显然用区间数表示目标威胁量值显然更合理。

定义1: 若∀aL,aU∈R且aL≤aU，称闭区间[aL,aU]为实数域R上的区间数；

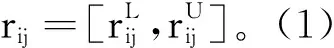
(1)

(2)

信息熵是系统无序程度的度量，信息熵越小，表明指标值的变异程度越大，指标权重就越大。将信息熵引入目标威胁评估指标权重的确定，更能客观反映各个属性对于目标威胁评估的影响。

定义2:设一个随机试验M由多个事件X={x1,x2,…,xn}组成，事件的概率为Pi，那么信息熵:

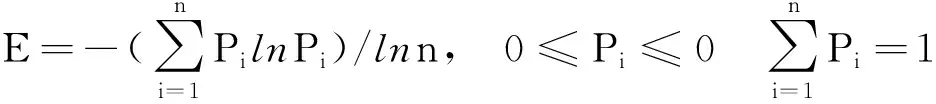
(3)

首先将规范化决策矩阵归一化得：

(4)

代入信息熵公式(3)得：

(5)

(6)

在防空作战中，在重视战场客观态势的同时，也要充分考虑指挥作战人员的主观经验和偏好。假定专家给出的主观权重(由层次分析法可求得)为θj。综合考虑主观权重和客观信息熵权，则评估指标的综合权重为:

(7)

3 信息熵和主观偏好综合求权的目标威胁评估

在指标权重确定之后，可直接采用线性加权的方法求出各目标的威胁评估结果，但当决策矩阵中各属性的测度值比较接近，使用线性加权的方法计算出的各目标的威胁度区分不明显。本文利用模糊决策理论，建立各目标与正理想目标的相对偏差关联系数的数学模型。首先对理想值和相对偏差定义。

定义3:设规范区间数决策矩阵R=[rij]n×m，正理想目标为各指标正理想值(最大值)的集合rmax，负理想目标为各指标负理想值(最小值)的集合rmin。区间数决正负理想值为：

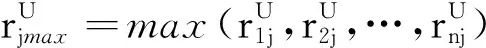
决策矩阵元素与正理想值之差称为正向相对偏差δijmax，决策矩阵元素与负理想值之差称为负向相对偏差δijmin。

用式(7)求得区间数综合指标权重ωj， 则目标xi与正负理想目标的加权相对偏差为:

(7)

若目标的正向加权相对偏差越小，说明该目标越优；负向加权相对偏差越大，则该目标越优。但若只通过比较各目标的正向加权相对偏差来排序威胁评估结果。有时会出现目标xi的正向加权相对偏差比目标xj小，同时目标xi的负向加权相对偏差也比目标xj小的自相矛盾的结果。为解决这一问题，本文引进了关联系数的概念，并建立了目标函数。

设αi为目标xi对于正理想目标的关联系数，则(1-αi)为相对于负理想目标的关联系数，αi值越大，表示目标xi与正理想目标关联度越大，威胁度就越大。构造目标函数F(α)应满足所有目标的正向加权相对偏差和负向加权相对偏差之和的总偏差最小。即:

(8)

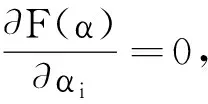
(9)

由αi定义，可根据αi的值从大到小对目标威胁评估结果排序。

4 仿真分析

为验证本文提出的目标威胁评估计算方法合理性，选取文献[6]中算例的5批测量数据进行验证，测量数据如表1所示。为便于比较排序结果，目标批号仍按照文献[6]中的批号标记。

表1 空中目标各属性测量值

威胁评估计算步骤如下：

(1) 将指标体系中的定性属性利用9级量化法转变成区间数形式。目标类型量化为[7,9]、[4,6]和[2，4]。干扰能力量化为[7，10]、[4，6]、[1，3]和[0,1]。

(2)利用式(2)和式(3)对进行规范化处理。获得决策矩阵为R=[rij]n×m。

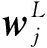
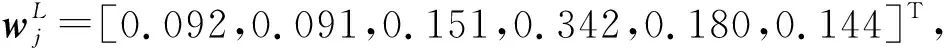
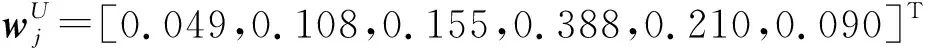
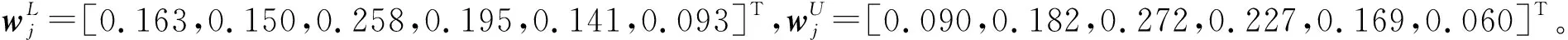
(5) 找出决策矩阵的理想值，然后利用式(7)求得目标xi的正向和负向相对加权偏差，则:

[0.050,0.053,0.010,0.013,0.043]

[0.019,0.016,0.049,0.056,0.015]

按照正向相对加权偏差，对目标威胁排序为(4,5,7,1,2)；按照负向相对加权偏差，对目标威胁排序为(5,4,1,2,7)。显然这两种结论是相互矛盾的，需要计算每个目标对于正理想目标的关联系数。

(6) 利用式(8)即可求得每个目标对于正理想目标的关联系数α,α=[0.275,0.232,0.831,0.811,0.259]将αi的值从大到小排序可得α3>α4>α1>α5>α2。采用原目标批号标注各目标，即可得目标威胁度从大到小排序为(4,5,1,7,2)。此排序结果与文献[6]中的排序结果基本一致。从而证明了该方法上无论是从理论分析还是与其他方法比较，都是合理有效的。

5 结 论

本文提出一种信息熵权和主观经验相结合求指标权重的方法。兼顾了客观态势排序和决策者主观偏好两方面的优势。综合考虑各目标的正向加权相对偏差和负向加权相对偏差，通过比较各目标对于正理想目标的关联系数，进行威胁评估和排序。避免了单一比较正向加权相对偏差而可能出现的自相矛盾的评估结果。该方法简单实用，编程易实现。为防空作战辅助决策提供了有效的科学依据。

[1] 陈克，刘士场，王幸军. AHP法改进及其在目标威胁等级评估中的应用[J].指挥控制与仿真，2006，28(1):108-110.

CHEN Ke, LIU Shi-chang, WANG Xing-jun. Application of AHP improvement for target threat grade estimation[J]. Command Control & Simulation, 2006,28(1):108-110.

[2] ZHI Jun, LIU Jian-yong, FU Cheng-qun, et al. Evaluation of aerial target threat degree based on Improved grey Interrelated analysis method[C]//Proceedings of 2009 IEEE International Conference on Grey Systems and Intelligent Services.Nanjing:[s.n.],2009.

[3] 申卯兴,许进，王帅. 空中目标威胁排序的灰色聚类决策方法[J].系统工程与电子技术，2008，30(9):1721-1723.

SHEN Mao-xing , XU Jin, WANG Shuai. Grey cluster decision making way for the threat ordering of aerial targets[J]. Systems Engineering and Electronics, 2008，30(9):1721-1723.(in Chinese)

[4] 童奇，童中翔，谷向东，等.基于信息熵的空战目标威胁评估[J].数学的实践与认识 2011,41(3)：144-148.

TONG Qi, TONG Zhong-xiang, GU Xiang-dong, et al. Target threat assessment for air combat based on information entropy[J].Mathematics In Practice And Theory, 2011,41(3)：144-148.(in Chinese)

[5] WEN Tang, CHEN Ai-zu, DONG Mei-li, et al. The application of combination weighting approach in multiple attribute decision making[C].Baoding: Proceedings of the Eighth International conference on machine learning and cybrnetics,2009.

[6] 郭辉,徐浩军.周莉.基于区间数TOPSIS法的空袭目标威胁评估[J].空军工程大学学报:自然科学版.2011,12(1)，40-45.

GUO Hui, XU Hao-jun, ZHOU Li. Evaluation of air attack threat against target based on interval numbers topsis[J]. Journal of Air Force Engineering University:Natural Science Editon. 2011,12(1),40-45.(in Chinese)