分段线性函数及其应用研究

庄方敏，黄若婷，陈满春

（韩山师范学院数学与应用数学系，广东潮州 521041）

在如股票分析，气象预测，混沌系统的构造、汽车建模参数分析，非线性电路设计等问题，经常会利用曲线来表示数据的波动，从而揭示问题的走向或本质[1].这些问题有些可以直接转换成分段线性函数的相关问题，有些则可通过分段线性函数来拟合逼近.

Brouwer不动点定理在学术上也受到学者的青睐.利用Brouwer不动点定理，严格证明了经济的一般均衡的存在性和最优性，使其在经济学上形成一个统一的方法和分析框架[2].Vasile listratescu在文献[2]的第四章的思路，完善了Brouwer不动点定理的泛函分析证明方法，并运用Brouwer不动点定理证明了纯交易市场下一般经济均衡的存在性.某种特定的情况下，利用不动点定理证明市场经济中的盈亏平衡点（BEP），从而规避投资的风险.盈亏平衡点越低，表明项目适应市场变化的能力越大，抗风险能力越强[3].

本文将主要研究用分段线性连续函数逼近连续函数的问题，并研究是否可通过求分段线性连续函数的不动点来得到相应连续函数的一个不动点的近似值，且误差在预定范围内.

1 预备知识

1.1 n段线性连续函数的相关定义

定义1 设 a=x0＜x1＜x2＜…＜xn=b， y0,y1,y2,……yn∈[ ]a,b，参数方程称为定义在[ ]a,b上的一个分段线性连续函数，记为y=ℓn(x)，其中xi,i∈{0 ,1,……,n-1,n} 称为ℓn(x)的分段点，有n+1个分段点的分段线性连续函数称为n段线性连续函数.

为了简单起见，ℓn(x)有时也表示为：(x ,y)=(xi+1,yi+1)λ+(xi,yi)(1 -λ).

I=[0 ,1]表示单位闭区间，为了研究的方便下面以I上的n段线性连续函数为主要研究对象.

设f:[0 , 1]→[0 ,1]是实值连续函数，对任意正整数n，用Ln(x)表示一个n段线性连续函数满足如下条件：为分段点，且L(x)=f(x),i=0,1,2,……,n.nii下文中若无特殊说明，一般用{Ln(x) }表示这样一列与 f(x)相对应的函数.

1.2 函数列一致逼近与一致收敛

定义2[4]设连续函数列{ fn(x) } 与连续函数 f(x)都定义在I上，若∀ε＞0,∃N＞0，使得当n＞N时，有则称函数列{fn(x)}在I上一致逼近于f(x).其中称为用fn(x)拟合f(x)的误差.

上述定义也可简单表述为：{fn(x)}一致逼近于 f(x)⇔（等价于）nli→m∞τn=0.

定义3[5]设函数列{(x)}与函数f(x)定义在同一数集D上，若∀ε＞0,∃N＞0，使得当n＞N时，对于一切x∈D都有|fn(x)-f(x)|＜ε，则称函数列{ fn(x)}在D上一致收敛于 f(x).

1.3 布劳威尔（Brouwer）不动点

定义4[6]设K是实数集R的子集， f:K→K是K到K自身的函数，若存在一点x∈K，使得f(x)=x则称 f(x)存在布劳威尔不动点，并称x是 f(x)的一个布劳威尔不动点，简称不动点.

关于不动点有下面著名的结论.

定理1[6]函数F(x)是闭区间[a , b]到[a , b]上的连续函数，则F(x)至少存在一个不动点.

2 主要结论

2.1 用分段线性连续函数逼近连续函数

定理2 设f(x)是I到I上的连续函数，则函数列{Ln(x) } 一致收敛于 f(x).

证明 由于f(x)在I上连续，则 f(x)在I上一致连续.即对于任给的ε＞0，存在着δ(ε )＞0，对于任意 x′,x″∈[0 ,1] 只要 | x′-x″|＜δ(ε)，就有 | f(x′)-f(x″)|＜ε.

因为min{ f (ai),f(ai+1) }≤Lni+1(x)≤max{ f (ai),f(ai+1) },

其中Lni+1(x)表示[ai,ai+1]上对应的函数段，即 (i + 1)第段线性函数.所以，

其 中 fi+1(x)表 示 f(x)在[ai,ai+1]上 对 应 的 函 数 ， 即 |fi+1(x)-Lni(x)|＜max则对于有 | f(x)-Ln(x) |＜ε成立.故在[0 , 1]上，存在函数列{Ln(x) } 一致收敛于连续函数 f(x).

下面引理说明一致收敛与一致逼近的关系

引理1 设连续函数列{ fn(x) } 与连续函数 f(x)都定义在I上，{ fn(x) } 一致收敛于 f(x)，则{ fn(x) } 一致逼近于 f(x).

证明 由于{ fn(x) }一致收敛于f(x)，对于任给的ε＞0，存在着N＞0，当n＞N时就有对任意x∈I成立，所以即{ fn(x) } 一致逼近于 f(x).

[注1]这个引理证明了一致收敛是一致逼近的充分条件.但一致收敛并非一致逼近的必要条件.例如，取 fn(x)=(1 -x)n,f(x)=0,x∈[0 , 1]，则即 fn(x)一致逼近于 f(x).但对任意n∈N+， | fn(0)-f(0)|=1，所以{ fn(x) } 不一致收敛于 f(x).

由定理2和引理1可得下面的推论.

推论1 对于I到I的连续函数 f(x)，分段线性函数列{Ln(x) }一致逼近 f(x).

2.2 利用分段线性连续函数的不动点

本节主要研究是否可以找到某个分段线性连续函数的不动点作为连续函数不动点的近似值.为此，证明了下面的结果.

定理3 设f(x)是I到I的连续函数，则对任意的实数ε＞0，存在N＞0，当n＞N时，若x∗是Ln(x)的一个不动点，则存在 f(x) 的一个不动点 x′满足 | x∗-x′|＜ε .

大力开展森林防火宣传工作。一是投入110万元，采购森林防火智能预警卡口100个，安装在重点林区关键地段，及时监测进入林区的人员和车辆；二是制作安装大型森林防火警示牌140个，提醒进山人员注意森林防火；三是编制印刷《森林防火宣传手册》、《防火通告》、《倡议书》等宣传材料11万份，发放到全市各林区，努力营造良好的森林防火氛围。

（1）若 x∗是 Ln(x)的分段点，则 f(x∗)=Ln(x∗) =x∗，取 x′=x∗即可.

（2）若 x∗不是 Ln(x)的分段点，则x∗落在某个分段区间[ai,ai+1]的内部中.

若ai+1是不动点，则该点也是 f(x)的不动点且与x∗的距离不超过ε.

若ai+1不是不动点，则 f(ai+1)≠ai+1,所以 f(ai+1)-ai+1＞0或 f(ai+1)-ai+1＜0.

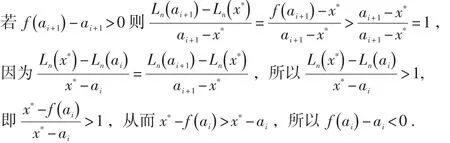
同理可证若 f(ai+1)-ai+1＜0则 f(ai)-ai＞0，即 f(ai+1)-ai+1与 f(ai)-ai总是异号.

因为f(x)-x在[ai,ai+1]上连续，由零点定理知，存在x′∈(ai,ai+1)使得 f(x ′)-x′=0.x′即为所求.证毕.

[注2]本定理可通过求分段线性连续函数的不动点作为求相应函数一个不动点的近似值.

取N2＞0，使得当k＞N2时，有此时

取N=max{N1,N2}，则当n＞N时，有公式（1）、（2）同时成立；

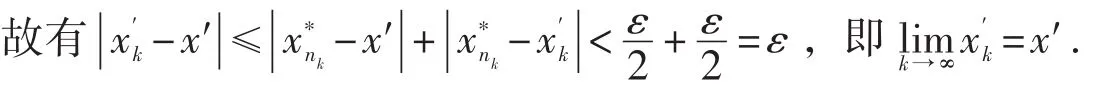
2.3 分段线性连续函数的不动点算法

若 y=ℓn(x)是I→I上的一个分段线性连续函数，则由定理1知ℓn(x)存在不动点，如果知道ℓn(x)的表达式，可以找出ℓn(x)的所有不动点.

设 y=ℓn(x)的表达式是其中

0=x0＜x1＜x2＜…＜xn=1,y0,y1,y2,……,yn∈[ ]0,1，皆为已知的数.

任取i∈{ }

0,1,……,n-1，下面分情况讨论

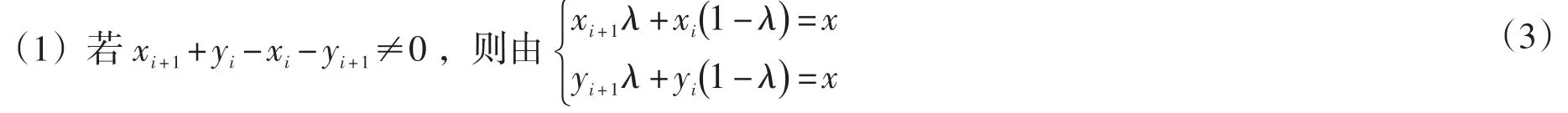
可求出

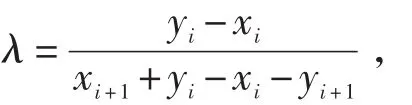
若 λ∈[0 , 1] ，则 x∗=xi+1λ+xi( 1 -λ)∈[xi,xi+1]且 ℓn(x∗) =x∗，所以 x∗是 ℓn(x)在[xi,xi+1]上的唯一不动点.

若λ∉[0 , 1]，则ℓn(x)在[xi,xi+1]上没有不动点.

（2）若xi=yi且xi+1=yi+1，此时对任意λ∈[0 , 1]方程组（1）都成立，因此[xi,xi+1]上的点都是ℓn(x)的不动点.

（3）若 xi+1+yi-xi-yi+1=0且 xy≠yi，此时ℓn(x)在[xi,xi+1]的图像是一段斜率为1的线段，ℓn(x)在[xi,xi+1]上没有不动点，若不然，方程组（3）有解，将方程组（3）的两个方程相减得(xi+1+yi-xi-yi+1)λ+xi-yi=0，即 xi=yi这与 xi≠yi矛盾.

[注1]根据上面的分析，可知一个分段线性连续函数，在每一个分段区间上的不动点只有三种情况：要么没有不动点，要么只有一个不动点，要么整个区间上的点都是不动点.

利用matlab软件按上述不动点的算法可编写求分段线性连续函数所有不动点的程序，程序见附录.

3 相关结论的应用

例1 对于市场中的某单一商品，设其对应的供给曲线为x(t)，需求曲线为y(t)，如图1所示.厂家该如何确定生产数量.

在经济学中，供给曲线就是边际成本曲线，需求曲线就是边际收益曲线，市场力量总会把该商品市场推向均衡，即图1中的A点，从而实现资源的有效配置.[4]

对于给定的数量t，会有相应的x(t),y(t)与之对应，利用matlab，画出以x(t),y(t)为坐标轴的散点图，利用拟合工具进行拟合，求出需求与供给的关系式 f(x).由定理3和定理4，存在分段线性函数{Ln(x) }一致逼近f(x)，利用程序求出ln(x)的不动点，该点可近似看成 f(x)的不动点，即为所求.

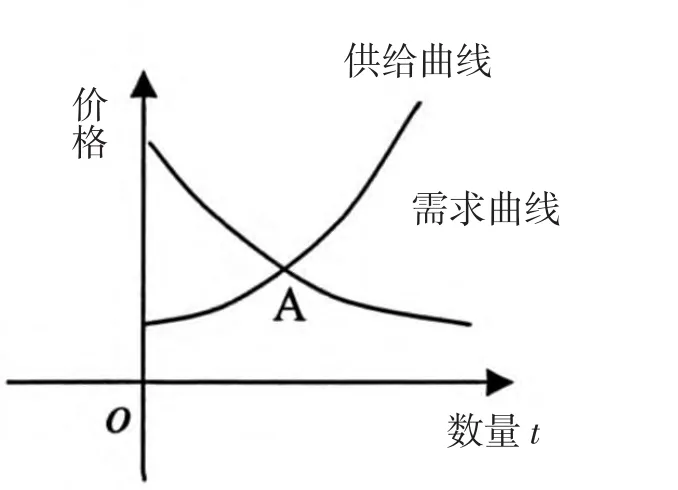
图1 供需均衡曲线图

[1]韩文蕾.中国股票市场的非线性分析规划[D].西安：西北工业大学，2006：22-24.

[2]ISTRATESCU V l.Fixed PointTheory(Au Introdurium)[M].Reidel，1981.

[3]迈克尔·帕金，罗宾·巴斯.微观经济学原理（第二版）[M].北京：中国人民大学出版社，2001：90-134.

[4]张韵华，奚梅成，陈效群.数值计算方法与算法（第二版）[M].北京：科学出版社，2006.

[5]华东师范大学数学系.数学分析（下册）（第三版）[M].北京：高等教育出版社，2001：26-36.

[6]张奠宙，顾鹤荣.不动点定理[M].沈阳：辽宁教育出版社，1998：35-150.

附录

Matlab求不动点程序编码：