基于第二代曲波的人脸识别算法研究

赵庆敏,辜道平

(南昌大学信息工程学院，中国 南昌 330031)

人脸识别属于一种生物特征识别技术，在安防监控、用户认证、人机交互等方面有着非常广泛的应用[1]．人脸识别算法已经得到广大科学家的普遍关注，并且产生了许多优秀的人脸识别算法，例如，特征脸算法，二维主成分分析算法，基于四元数Gabor小波的彩色人脸识别算法[2]等．二维主成分分析算法直接计算图像协方差矩阵的特征向量，能够准确地计算协方差矩阵[3]．二维主成分分析算法的主要不足之处就是需要较多的系数来进行图像表征，因此，该算法得到了改进，加权变形的二维主成分分析人脸识别算法及改进的模块二维主成分分析人脸识别算法[4]．双向二维主成分分析法可以同时利用行和列上的投影矩阵，在利用较少的图像表征系数的前提下可以获得与二维主成分分析法相同或者更高的识别率[5]．

基于小波加权的双向二维主成分分析人脸识别算法是比较优秀的一种人脸识别技术，通过小波变换对人脸图像进行小波分解，对低频子带加权后将低频子图代替原始人脸图像，不仅能够降低数据维数，而且能够抑制随机噪声[6-7]．小波变换通常被称为“数学显微镜”，具有多分辨率的特点，已经被成功地应用于人脸识别算法中，然而小波变换不具有各向异性的特点，仅仅能反映一维信号中奇异点的性质，进而无法表达二维图像的“沿”边缘特征[8]．Candès和Donoho提出的曲波变换的在很大程度上弥补了小波变换的缺陷，能够较好地表示直线奇异和曲线奇异特征[9]，但是第一代曲波的实现过程具有较高的时间复杂度，而且容易出现较大的数据冗余量．因此，Donoho等人于2005年又提出了第二代曲波变换[10]．第二代曲波以其良好的细节表达能力可以有效地应用于人脸识别算法中，但是非线性变换过程中需要对多个参数进行调节，进而增加了人脸识别的复杂性.同时，变换函数在进行第二代曲波系数变换时没有考虑到尺度不同分布特征不同的特点，在人脸识别时存在着一定的缺陷．为了能够提高人脸识别的效果，提出了一种改进的基于第二代曲波加权的双向二维主成分分析人脸识别算法．

1 第二代曲波的基本理论

设在笛卡尔坐标系统下的输入为f(t1,t2)，0≤t1,t2≤n，第二代曲波变换的离散形式可以表示为如下的形式[11]：

对于任意一个ω=(ω1,ω2)，ω1>0，有如下公式成立：

Vj(Sθlω)=Vj(2⎣j/2」ω2/ω1-l)，j>0,

式中，⎣j/2」表示j/2的整数部分，Sθl表示剪切矩阵：

式中:tanθl=l·2⎣j/2」，l=-2⎣j/2」,-2⎣j/2」+1,…,2⎣j/2」-1．θl的斜率是等间距的，对于每个θl∈[-π/4,π/4]，有如下公式：

2 基于第二代曲波变换的加权算法

2.1 Wrapping算法的基本原理

Candès和Donoho设计了2种快速离散曲波算法，一种是USFFT算法，另外一种是Wrap算法．基于Wraping的快速离散曲波变换算法如下[12]：

(1)在给定笛卡尔坐标系下，对二维函数做2DFFT变换所得到的二维频域表示为

(5)对上一步结果进行2DIFFT变换，可获得离散曲波因子的集合cD(j,l,k)．

图1 Wrapping快速离散曲波变换的原理图 Fig.1 Theory diagram of Wrapping fast discrete curvelet transformer

Wrapping算法的核心思想如下[13]：利用频率周期化技术将任意区域映射到原点的仿射区域中，形成一一对应的映射；2DIFFT变换通过把图1的椭圆从原点开始进行映射，从而获得矩形区域，此时，可以利用二维数组表达．

2.2 改进的第二代曲波非线性加权算法

基本的Wrapping人脸识别方法存在2个缺陷：

(1)图像信息通常位于边缘，利用第二代曲波进行降噪时由于其具有平移不变性，将导致系数的“过扼杀”，从而使图像边缘产生“振铃”效应．

(2)由于曲波变换具有“楔形基”的特性，因此变换因子具有一定的相关性，当系数变化时将改变空域中一条直线上的全部值，因此使图像失真．

针对以上缺陷，建立基于第二代曲波的图像加权算法，算法流程如下所示：

步骤1：利用下式对二维图像进行归一化：

步骤2：图像经过归一化处理以后，按照直方图的图像分类确定Beta函数中的参数α和β，并且进行如下的变换：

g′(i,j)=F(g(i,j)),

式中，F(·)表示非完全Beta函数变换．

步骤3：对g′(i,j)进行反归一化处理，获得相应的图像x(i,j)．

步骤4：利用第二代曲波变换对图像x(i,j)进行分解；

步骤5：分解后的低频和中频曲波系数利用如下的公式进行非线性变换：

对分解后的高频曲波系数利用软阈值函数做降噪处理，软阈值函数可以表示如下：

步骤6：做第二代曲波反变换获得人脸识别结果图像x′(i,j)．

3 基于第二代曲波加权的双向二维主成分分析人脸识别算法

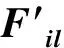
式中，L表示人脸识别的特征矩阵．

4 实验结果及分析

为了能够验证算法的有效性，从ORL和Yale人脸数据库选取人脸图像样本，ORL人脸数据库的基本信息为：人脸总数为400张；共分类40类，图像尺寸为112×92，影响人脸识别的因素为表情、饰物和姿势．Yale人脸数据库的基本信息：人脸总数为165，一共有15类，图像的尺寸为100×100，影响人脸识别的因素有表情，光照、饰物和姿势．样本图像如图2和图3所示．

图2 ORL人脸数据库的样本图像 图3 Yale人脸数据库的样本图像Fig.2 Sample diagram of OLR face database Fig.3 Sample diagram of Yale face database

为了能够验证该算法的有效性，分别利用小波加权双向二维主成分分析算法和第二代曲波加权的双向二维主成分分析算法对以上两个人脸数据库进行人脸识别．在实验前，对所有人脸的数据进行归一化处理，在实验过程中对特征向量进行单位化处理．

在ORL人脸数据库选取150张人脸图像作为训练集合，其余250张人脸图相作为测试集合．在Yale人脸数据库选取60张人脸图像作为训练集合，其余105张图像作为测试集合．在不同的特征矩阵的维数下，分别任意地进行20次实验，仿真实验利用MATLAB软件实现，相应的实验结果见表1和表2．其相应的人脸识别仿真曲线如图4和图5所示，表及图中的识别率为20次实验的平均识别率．

表1 ORL人脸数据库的性能仿真结果

表2 Yale人脸数据库的性能仿真结果

从表1和表2的结果可以看出，对于ORL人脸数据库，特征向量维数为8时，第二代曲波加权的双向二维主成分分析人脸识别算法的平均识别率最高，可以获得较好的人脸效果，识别时间最少，因此具有较好的算法优势．Yale人脸数据库，当特征向量维数为12时，平均最佳识别率最高，并且所用的识别时间也最短，因此，第二代曲波加权的双向二维主成分分析算法明显优越于小波加权双向二维主成分分析算法．

图4 ORL人脸数据库的识别仿真曲线 图5 Yale人脸数据库的识别仿真曲线 Fig.4 Identifying simulation curve of ORL face database Fig.5 Identifying simulation curve of Yale face database

从图4和图5可以进一步看出，第二代曲波加权的双向二维主成分分析算法在人脸识别率上明显优越于小波加权双向二维主成分分析算法．

5 结论

将改进的基于第二代曲波加权的双向二维主成分分析算法应用于人脸识别中，建立了算法流程．以ORL人脸数据库和Yale人脸数据库为例进行了仿真分析.仿真结果表明，改进的人脸识别算法具有较好的人脸识别效果，与传统的人脸识别算法相比，不仅提高了识别率，而且缩短了识别时间，在人脸识别中具有广阔的应用前景．

参考文献：

[1] 李苗在，谷海红. 人脸识别研究综述[J]. 电脑知识与技术, 2011,7(24):5992-5994.

[2] 郎方年，周激流. 四元数矩阵正交特征向量系的求解方法及其在彩色人脸识别中的应用[J]. 自动化学报, 2008,34(2):121-129.

[3] YANG J, ZHANG D, FRANGI A F,etal. Two-dimensional PCA: A new approach to appearance-based face representation and recognition[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2004,26(1):131-137.

[4] 贲晛烨，安 实，王科俊,等．改进的完全二维主成分分析及其在步态识别中的应用研究[J]. 计算机应用研究， 2011,28(6):2088-2091.

[5] ZHANG D Q, ZHOU Z H. (2D)2PCA: Two-directional two-dimensional PCA for efficient face representation and recognition[J]. Neurocomputing, 2005,69(1-3):224-231.

[6] 彭义刚，谢旭东，徐文立,等. 基于小波变换的人脸识别技术综述[J]. 测控技术, 2009,28(5):7-10.

[7] 曹 雪. 小波理论在人脸识别中的应用研究[D]. 南京：南京理工大学， 2012.

[8] 焦李成. 图像多尺度几何分析[M]. 西安: 西安电子科技大学出版社， 2008.

[11] 王 宪，慕 鑫，张 彦,等. 基于曲波域与核主成分分析的人脸识别[J]. 光电工程, 2011,38(10):98-102.

[12] 闰敬文，屈小波. 超小波分析及应用[M]. 北京：国际工业出版社， 2008.

[13] 贾西贝. 基于曲波变换的人脸识别算法研究[D]. 哈尔滨：哈尔滨工程大学， 2011.

[14] 李 童. 基于改进的2DPCA人脸识别方法研究[J]. 重庆工商大学学报:自然科学版, 2012,29(4):45-49.

[15] CHIEN J T, WU C C. Diseriminant wavelet faces and nearest feature classifiers for face recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002,24(12):1644-1649.