磁异常化极效果的研究

王浩臣， 刘庆成， 邓居智， 陈 辉， 李 磊

(东华理工大学 放射性地质与勘探技术国防重点学科实验室，江西 南昌 330013)

根据磁异常的数学物理特征，对实测磁异常值进行必要的数学加工处理，并借助于计算机技术，使之满足某些特定需要的过程称之为磁异常的转换和处理过程。这已成为磁异常解释和推断中不可或缺的重要步骤(罗孝宽等，1991)。通过对磁异常的处理，满足磁异常解释推断方法的要求，经过处理，突出有用的信息，压制干扰信息，有利于增加推断解释的准确性(黄临平等，1998)。但磁异常的实际情况往往是复杂的，解释推断的要求在不断提高，推断的方法也在不断改变，这就要求能从多方面提供异常信息，来满足推断方法本身的要求。

由于地球地磁倾角的变化，地质体的磁化方向随着纬度的变化而变化。同一个地质体，不同的磁化方向所产生的磁异常也不一样，这就增加了磁异常解释的复杂性，把斜磁化的磁异常化为垂直磁化，即通常所说的化到地磁极，在磁异常的数据处理方法中占有重要的地位(袁照令等，1998)。

磁异常化极作为一种重要的数据处理方法，很早就受到地球物理工作者的重视和研究。最早研究化到地磁极的是Baranov(1957)，通过空间域卷积形式近似对磁异常进行化极，其方法计算及过程相当复杂。对磁异常进行解释和推断的目的就是为了确定磁异常体的形状和位置。目前磁异常化极的方法有很多种，化极的效果也有好有坏，将磁异常化极需要知道地磁场方向和磁性体的磁化方向。一般来说，磁化方向是难以知道的，化极时通常是假定磁化方向与地磁场方向一致，但是由于剩余磁化强度的存在和退磁作用的结果，磁性体的磁化方向与地磁场方向不一致，以致化极结果不准确。数据的离散性及有限性和磁化方向不准是影响磁异常化极效果的两个主耍原因(王纪恒，1993)。通过公式来分析十分困难，只能通过模型试验判断是否有效，因此需要研究磁异常化极前后三维反演效果的好坏。

1 基本理论及方法简介

重磁数据的处理是重磁勘探的重要环节，通过合理使用数据处理方法，可以有效提炼出有用的信息，有助于发现异常、解释异常。

线性反演方法可以用来寻找一个模型m，其满足条件:

式中，G 为万有引力常数，用来描述物理问题。dobs为观测数据矢量。在位场数据中，对含有M个单元体的地下模型(m)进行离散化，其中M 值通常大于数据量N，即可得到(dobs)。这个结果在N ×M(M ＞N)的矩阵G 中不是矩形，所以这个矩阵是不可逆的。因此，这变成了一个优化问题，寻求一个解决方法，同时最大限度的减少观测模型的数据量以降低观测结果和预测结果之间的误差。

1.1 目标函数

磁法反演就是用模型的目标函数来量化模型的各种特性。目标函数的细节取决于具体的问题，并且可以随着先验信息的变化而变化，但是通常，目标函数应该具有一定的灵活性以使所构造的模型接近参考模型，并使构造产生的模型在三维空间內是平滑的。就现在掌握的地质知识，可以把参考模型描绘的更具体，一个完整物性模型，对于地下物性分布状况的预测是非常重要的。模型的目标函数使计算得到的反演模型的特性尽可能的接近参考模型。模型的目标函数定义为:

式中，第一个积分分量测量的是最小值。后面三个积分分量是参考模型mref的测量值。这些分量确保反演模型和参考模型之间的差异可以分散在整个区域内而不会单独存在一个网格体中。自定义参数αs，αx，αy和αz为各个方向上的相关性系数。加权函数ws可以使单元格内的物性值更接近参考模型，可以理解为对指定的单元格加入物理属性。同样，参数wx，wy和wz可以使模型结构在空间域内各个方向变化，以呈现真实的地质形态和地质边界。函数wr(z)则是深度或距离加权函数。

1.2 深度加权

观测的磁场是一个深部与前部地质体的叠加场，常规数据处理不能很好地反映场源随深度变化的细节，主要原因是位场幅值会随着场源深度的增加而迅速衰减。如果模型内没有加入地质资料，所观测到的潜在磁场响应中就不含有固定的深度信息，则会使模型的表面及其附近的数据含有较高的灵敏度。深度加权函数有两种形式(Li et al.，1996)。

深度加权函数只考虑在加权深度以下所观测到的地球物理数据。

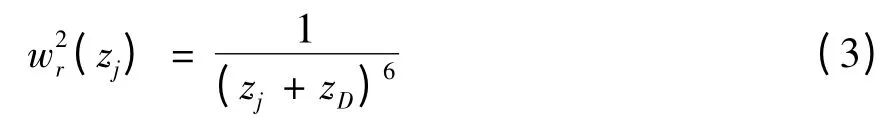
式中，z 是第j个网格单元的深度值，z0和β 是可以调节的参数，使加权函数的磁场强度和深度相协调。β是重现磁响应随着距离而变化的衰减指数，一般取值为3。参数z0是中心网格随地球物理磁场强度的大小变化，自动计算出来的值。这种方式适用于在地形平坦的地区观测高密度数据的一阶近似衰减异常。

加权函数的稳定式允许地球物理数据在不同地形下不规则分布的或离散分布，并对观测资料和单元格进行三分量分离。深度加权函数与特定单元格的分离观测磁场源的数据有关，包括其密度和灵敏度，可以与允许数据灵敏度在横向和垂直方向发生变化。

式中，Rij是第j 单元格和测量结果i 之间的距离，R0是一稳定系数。加权深度，参数β 是用来重现异常体随着深度变化所引起的磁场响应的衰减指数。取值为3。参数R0取值为最小单元格大小的四分之一，以确保加权距离始终在可定义范围内。

1.3 网格剖分

网格剖分即为网格模型的离散化，通过将地下半空间剖分成若干合适的矩形体(代表地质体单元)，组合形成三维模型区域(图1)。这样，其中任一地质体单元j 在坐标观测点p(x，y，z)的磁异常△gi(x，y，z)σj为:

式中，σj为第j个单元模型的密度差，p(k，l)为场源的几何参数与计算点坐标之间的关系，称之为几何格架。

在三维反演中，模型的剖分关系确定下来后，其几何形态及与测点的相对关系将保持不变。网格剖分时需要考虑模型的精度，以测网密度为主要参考，而测网密度与设计的地质体规模大小有关。从计算量来讲，如果将几何构架存储起来，那么原本海量的求解模型的正演计算就变得相对简单。

为了方便讨论，本文建立3个不同类型的简单模型，对其磁异常正演的结果数据进行不同磁化倾角的磁异常化极处理，对其处理结果进行三维磁法反演与原始磁异常数据的反演结果进行对比研究(图2)。

图1 地质体剖分模型图Fig.1 Subdivision of a geological body model a.组合模型;b.任一模型单元

图2 反演流程图Fig.2 Inversion flow diagram

2 磁法3D 模型反演效果及解释

为了方便讨论，本文建立三种不同类型的简单模型，并对其正演结果进行化极处理，再对化极前后的三维反演结果进行对比。三种简单模型分别为单个异常体模型、复合异常体模型和单个倾斜板体模型，其地质体模型及其所对应的磁法观测数据迭代误差如图3 所示。

2.1 单个异常体模型

建立一个含有单个磁性异常体的初始模型，通过对该模型进行磁倾角化极和无约束的磁法三维反演，并对化极前后的三维反演结果进行对比，验证其反演后的结果与所建立的磁性体模型是否吻合。对所建立的初始模型进行正演得到正演结果，对其正演结果进行磁法三维反演。

为了方便讨论，研究模型为自己所建立的。磁化强度则没有实际测量结果，假设地磁倾角为48.5°。用48.5°作为磁化倾角化极后，化极结果对比如图4 所示。a 是化极前的平面图，异常值线表现出来异常体的位置明显向南方向偏移，且南边等值线未封闭，有向外延伸趋势。化极后的磁异常如图4b 所示，异常体的位置明显向北移动，正异常南北侧封闭，东西向等值线有向外延伸现象，对比于化极前异常体的位置更接近于所建立模型的位置。说明化极后的结果更好的表现出了磁化异常体的异常特征，获得了合理的结果。

本文对化极前和以化极后的磁异常数据分别进行了磁法三维反演。反演计算中，各方向相关系数αs=0.000 1，αe=1，αn=1，αz=1，使其在三个方向的平滑度一致;参考模型采用零空间模型，即背景密度ρ 设置为0，反演的深度加权因子为1。未化极磁异常反演经过60 次迭代后，反演结束;磁倾角为48.5°化极后反演经过32 次迭代，反演结束。图4d 是三维反演结果的切片图，所展示的化极前和磁化倾角为48.5°化极后的反演结果。从反演结果中可以看出，化极前后的区域内都有明显的深色异常体。化极前的反演切片图4c 中显示异常体位于反演区域内的南侧，与所建立的模型有一定的偏差，当磁化倾角为48.5°时，图4d 所表现出来的异常体非常明显，且在反演区域内的位置也与建立的模型中异常体的位置基本一致。相对于化极前的反演结果，化极后的反演切片图4d 中的磁异常信息与理论模型的磁异常分布对应较为准确，较好地反映出地下磁异常体及周围的真实信息。

2.2 复合异常体模型

对含有两个磁性异常体的复合异常模型进行磁倾角化极和无约束的磁法三维反演。同样对初始模型进行正演得到正演结果，对其正演结果进行磁法三维反演。

对正演结果进行磁倾角为48.5°的化极处理，所得到的结果如图5 中所示，5a 为未化极结果，图中可以看出正异常等值线南侧向外延伸，表现出位置向南侧偏移的形态，与图5b 磁化倾角为48.5°的化极结果相比较，化极后的结果较好的显示出异常的形态且异常等值线均为闭合状态。

设置同样的反演参数对模型进行反演，未化极磁异常的迭代次数为60 次，磁倾角为48.5°的反演迭代次数为32 次。反演结束。得到的磁法三维反演结果如图5 中所示。通过对比未化极的反演结果图5a 和磁化倾角为48.5°的化极后反演结果图5d，在没有完全消除周围影响的情况下较准确的显示出了异常体的形态和位置。更好地反映出地下异常体的分布情况。

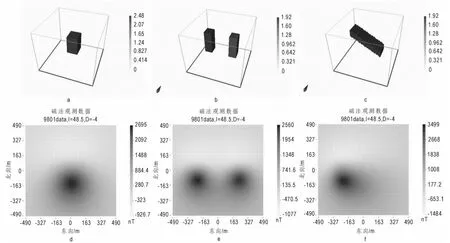
图3 地质体模型和观测数据迭代误差图Fig.3 Geological body model and iterative errors of observed data

图4 单个异常体模型磁异常磁倾角化极结果及3D 反演结果切片图Fig.4 Reduction to the pole of magnetic anomaly result of individual anomalies body and slices diagram showing 3D inversion result

2.3 单个倾斜板体模型

图5 复合异常体模型磁异常磁倾角化极结果及3D 反演结果切片图Fig.5 Reduction to the pole of magnetic anomaly result of composite anomalies and slices diagram showing 3D inversion result

图6 单个倾斜板体模型磁异常磁倾角化极结果及3D 反演结果切片图Fig.6 Reduction to the pole of magnetic anomaly result of individual sloping panel body and slices diagram showing 3D inversion result

为了更好地对比，所建立的含有单个倾斜板体异常模型，同样进行磁倾角化极和无约束的磁法三维反演。

首先对正演结果以磁倾角为48.5°进行化极，所得到的结果如图6 中所示，图6b 为磁倾角48.5°的化极结果，图中可以看出正异常位于数据区域的中间位置片西侧，向东方向逐渐减小，与建立的单个板体异常模型中异常体的位置基本一致。相对于化极前图6a 的结果，化极后区域内形态整体向北移动，且幅值增大。图6b 中化极结果较准确的显示出异常体的位置。

分别对原始正演结果和磁化倾角为48.5°化极后的结果进行三维磁法反演，经过60 次和32 次迭代后，反演结束。同上面两种模型反演结果一样，相对于化极前的反演结果(图6c)，化极后的磁异常反演切片(图6d)最为理想。

3 结论与建议

磁倾角化极的方法有很多，各有优缺点。本文中通过建立理论模型进行化极前后的三维反演结果对比表明，化极的磁化倾角选择很重要，如果磁化倾角过大或者偏小，都会导致非正常化极，会使磁异常发生畸变。对磁异常进行化极会使反演结果更接近于真实值，相对于未作化极处理的结果比较，化极后区域内的异常及周围介质都会整体向北向偏移，且幅值会增大。

本文仅通过建立简单磁异常体模型，进行正反演推断异常体信息，但反演得出的结果仅限于理论研究，在以后的工作中可以通过在实测数据中加入地质约束条件，使得反演结果得到更进一步的准确。如何将其他地球物理勘探方法所得的数据资料加入进行联合反演，建立含有地质耦合的三维反演模型，是今后研究的重点。

黄临平，管志宁. 1998. 利用磁异常总梯度模确定磁源边界位置［J］.华东地质学院学报，21(2):143-150.

罗孝宽，郭绍雍.1991.应用地球物理教程-重力，磁法［M］.北京:地质出版社.

彭利丽，郝天珧，姚长利，等.2010.低纬度磁异常滑稽方法应用效果对比［J］.地球物理学进展，25(1):151-161.

王纪恒.1993. 关于磁异常化极的若干体会［J］. 物探化探计算技术，15(4):333-338.

袁照令，李大明.1998. 关于磁异常化极到地磁极问题的几点认识［J］.物探化探计算技术，20(3):284-287.

Baranov W. 1957. A new method for interpretation of aeromagnetic maps:pseudo-gravimetric anomalies［J］. Geophysics，22(2):369-382.

Li Y，Oldenburg D W. 1996.3-D inversion of magnetic data［J］.Geophysics，61:394-408.