考虑剪胀和软化的巷道围岩弹塑性分析

魏建军

（1.中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州， 221008；2.江苏建筑职业技术学院 江苏省建筑安全与减灾工程研发中心，江苏 徐州， 221116）

随着矿山开采的大规模进行和采深的增加，造成的灾害日益增多，对深部资源的安全高效开采造成巨大威胁。深部岩体处于高地应力、高温、高渗透压的恶劣环境中，使得岩体的组织结构、力学性态和工程响应均发生根本性变化，围岩表现出特殊的非线性力学行为［1－3］。深部巷道开挖后二次应力场形成引起的高地应力集中导致围岩压剪应力超过其强度进而破坏处于剪胀状态；同时，开挖后的近表围岩内空隙水压力降低引起的围岩有效应力增大加剧了围岩的破裂；高地温带来的附加应力对围岩破裂扩展带了不可忽视的影响。岩石进入峰后阶段由于应力跌落方式的不确定性，难以用经典理论来描述［4－5］。Hoek等［6］于 1997年提出了估算岩石峰后力学行为的方法，给出了岩石峰后力学模型。随后，学者对围岩的弹塑性分析进行了大量研究。其他国家的研究集中于基于Hoek－Brown强度准则采用弹脆塑性模型进行分析［7－10］，中国的研究则考虑岩石的非线性软化和破坏过程，但在解析计算方面为了求解方便往往设置不合理的限制，如在围岩破坏过程中体应变设置为零［11－12］、弹性模量设为常数［13］等，这些方法均不符合巷道受扰变形的机制。

圆形硐室的轴对称弹塑性分析是个经典问题，有许多学者进行过研究。文献［8］对 Mohr－Coulomb介质中的应变软化过程进行了研究，其中考虑了黏结力和剪胀角的下降，内摩擦角在软化变形中保持不变；文献［7］将圆形硐室围岩内形成的塑性区划分为一系列的同心圆环，采用差分法求解得到软化区与残余强度区尺寸以及相应的位移分布；文献［14－16］考虑了统一强度理论，软化段采用双折线模型，得到了硐室围岩弹塑性分析的统一解。

本文根据岩土体材料在出现应力跌落以前或多或少要经过一段塑性变形的过程，考虑引入应力跌落条件阈值来判断是否出现应力跌落，构建一个弹塑脆性模型，考虑围岩的应变软化和剪胀特性，采用Mohr－Coulomb屈服准则对圆形硐室围岩进行弹塑性分析。

1 弹塑脆性模型及问题描述

前人所采用的应力跌落模型的应力 应变曲线由两段组成，即屈服前的线弹性阶段和屈服后的残余强度阶段，即认为材料在达到弹性极限之前为线弹性，一旦达到弹性极限，便会屈服，并且强度降为残余强度。其实，真正弹脆性材料是不存在的，材料在出现应力跌落以前，或多或少要经过一段塑性变形的过程。因此，本文采用弹塑脆性模型，如图1所示。巷道围岩应力 应变曲线可分为处于弹性区、塑性发展区和残余变形区3种状态。

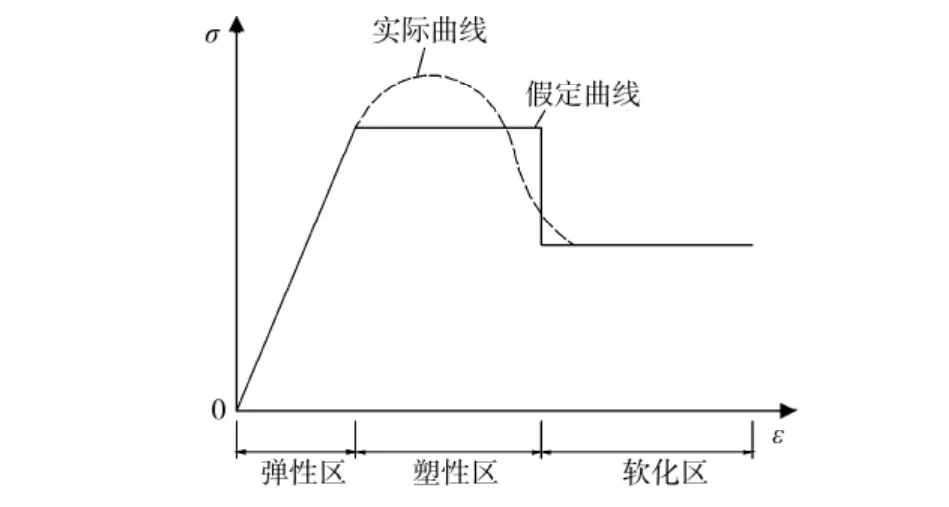
图1 岩石的应力应变曲线

模型以微元体中与最大主应力和最小主应力都成45°的面上的最大剪应变来描述岩石不可逆的塑性变形，当最大剪应变达到某一值时，材料即出现脆性软化，该最大剪应变的临界值即为软化阈值，其值在下文用γf表示。

本文研究岩土材料中平面应变条件下的圆孔问题。如图2所示，在弹塑脆性材料的无限空间中作用有静水压力p0，其中有一无限长圆形硐室，开挖半径为a；支护荷载为pi；随着围岩卸荷发展，硐室周围岩土体进入塑性，贴近洞口部分区域剪应变达到软化阈值，材料出现软化形成环形软化区，这样巷道围岩自内向外由软化区、塑性区和弹性区3部分组成，为书写方便，其对应的物理量分别附下标s、p、e以示区别。

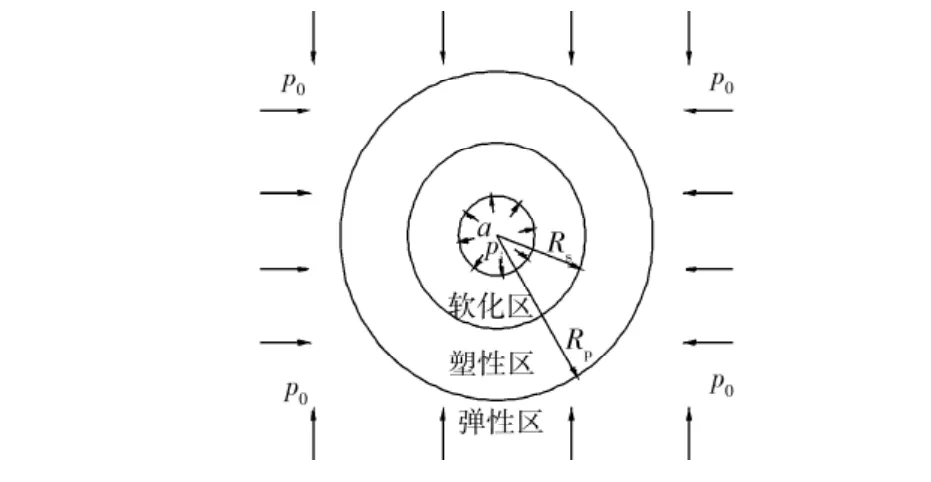
图2 圆形硐室围岩弹塑性分析模型

2 基本假定与方程

做如下基本假定：

1）围岩材料均匀、连续、各向同性。

2）材料屈服服从Mohr－Coulomb准则。

3）围岩材料具有明显的剪胀特性，塑性及软化区体积应变不等于0。采用线性剪胀模型，位移以指向洞内为正，设剪胀参数为βi，则塑性应变与的关系为：

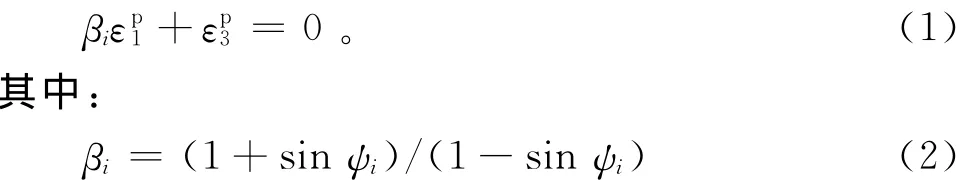
式中：ψi为剪胀角，一般小于或等于内摩擦角φ；i表征围岩所处区域。

4）围岩塑性软化区的泊松比为常数，弹性模量仅在软化区劣化，劣化系数k＝Es／Ee，取值范围0～1，可以通过地质探测资料获得。

在各区内围岩应力满足平衡方程：

岩石在出现塑性屈服和软化时，其应力满足Mohr－Coulomb准则，且认为围岩被动承受地压力，σθ＝σ1，σr＝σ3，在塑性区和软化区内统一表示为：

式中N和S为材料参数。

式中：ci、φi为黏聚力和内摩擦角；i统一表示围岩所处的不同区域。

应变公式为：

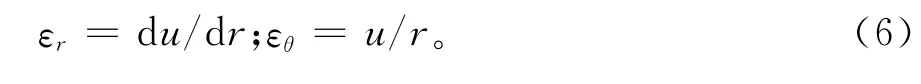
3 问题求解

3.1 软化区分析

在软化区（a≤r≤Rs）

式中：Ds＝Cscotφs。

由几何方程（6）、广义虎克定律及变形协调方程：∂εθ／∂r＝ （εr－εθ）／r可解出应变和位移表达式：

式中：ηs＝ （1－v）（Nsβs＋1）／（Ns＋βs）－v；βs为软化区剪胀参数；k为弹模劣化系数；A为积分常数。

3.2 塑性区分析

在塑性区（Rs≤r≤Rp）和软化区计算类似，可得塑性区的应力表达式为：

式中：ηp＝ （1－v）（Npβp＋1）／（Np＋βp）－v；B 为积分常数。

3.3 弹性区分析

在弹性区（Rp≤r＜∞）围岩的应力和应变为：

将式（13）中的A 和B 代回式（8）、（10），可得软化区、塑性区的应变和位移表达式。

3.4 巷道破坏半径的确定

确定巷道围岩破坏范围通常采用边界处应力或位移连续条件。本文在弹塑性交界处弹性应力满足塑性屈服状态，即：

将式（9）、式（11）的有关式带入式（14）可得：

式（15）建立了塑性圈半径和软化区半径的关系，尚需要再寻找一个条件方可确定其解。

围岩的破坏除了满足应力条件外还应满足变形条件。在判定围岩或地下结构稳定性时，常以洞周切向应变值来进行控制，即认为围岩的最大剪应变达到或超过允许值时围岩就破裂进入软化松动区。考察理想塑性区与软化区交界处塑性区一侧的剪应变，可表示为：

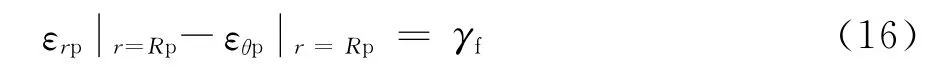
式中γf为塑性区围岩抗剪强度破坏时的应变值，对应于三轴试验测得的岩样相应的临界剪应变值。

由塑性区应变表达式（10）代入上式整理后得到塑性区围岩软化破裂的变形条件。

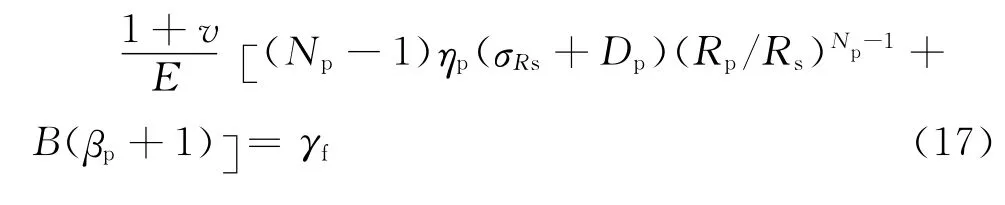
将式（15）和（17）联立即可获得软化区半径Rs和塑性区半径Rp。

4 算例与讨论

采用文献［17］的计算实例。贵州锦屏二级水电站大水沟厂房支1洞位于东雅砻江右岸，地质岩性主要为大理岩，截面尺寸为3.26m×3.30m（宽×高），近似为圆形硐室。经过地应力实测表明探洞断面上竖直主应力约为22.9MPa，水平主应力约为19.8MPa。

结合现场测试与设计院试验结果确定本研究段的岩体力学计算参数为：弹性模量Ee＝Ep＝16GPa，Es＝2GPa；泊松比υ＝0.3；在弹性区和塑性区粘聚力cp＝2.5MPa，摩擦角φp＝35°；在塑性软化区粘聚力cs＝1.4MPa，摩擦角φ＝23°。取剪胀角ψp＝18°，ψs＝13°，岩石的应变软化阈值分别取0.001、0.004、0.01。地应力近似为两向等压，取p0＝21MPa；支护荷载pi＝0。通过计算得到其对应的软化区及塑性区范围见表1。围岩的应力与应变分布如图3所示。

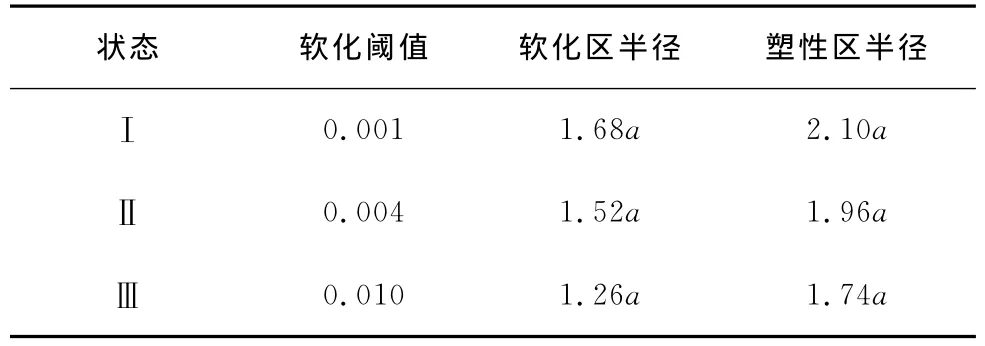
表1 塑性范围计算结果

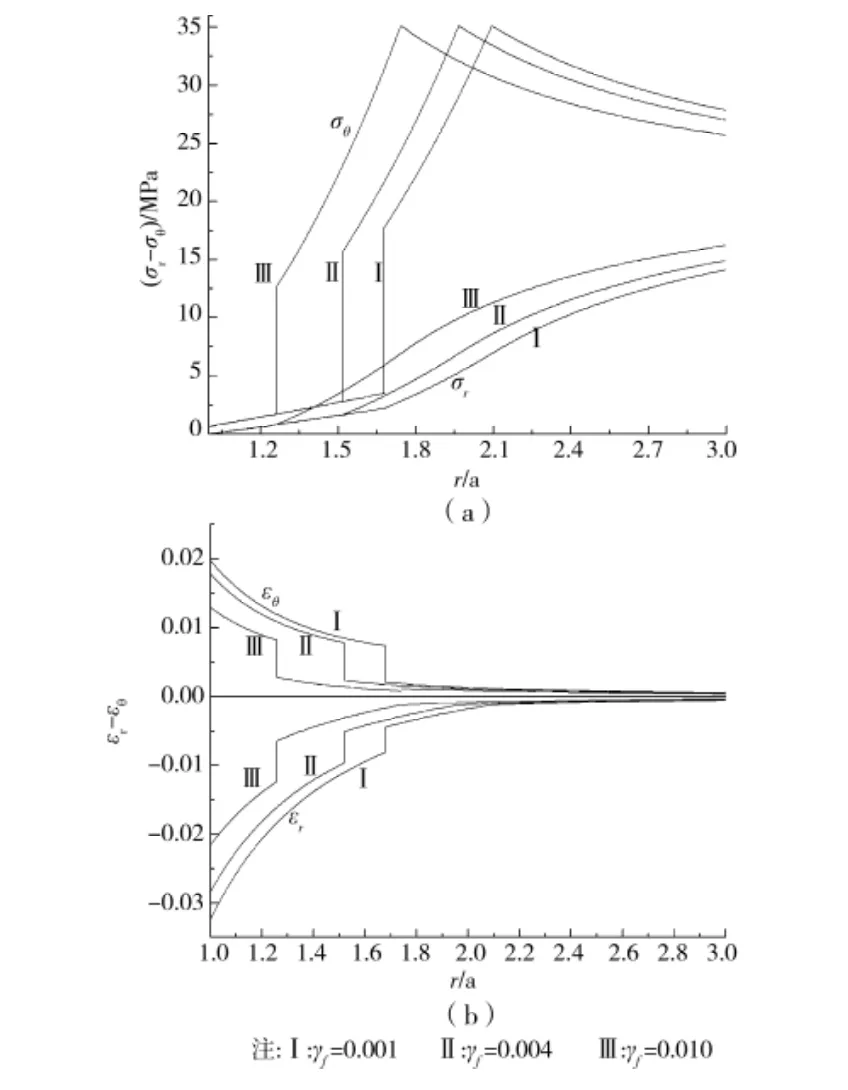
图3 软化阈值对围岩应力与应变的影响

从图3可以看出，软化阈值对分析结果影响显著，随着软化阈值减小，软化区和塑性区范围增大，在相同松动圈半径位置，应力随之减小，应变则增大。

图4为软化阈值取0.004时，围岩弹模劣化系数k分别取0.125、0.300、0.600三种情况下的应变曲线。从结果可以看出，近巷围岩弹模劣化是导致深部巷道围岩变形较大的因素之一，不考虑围岩弹模劣化计算结果偏危险。

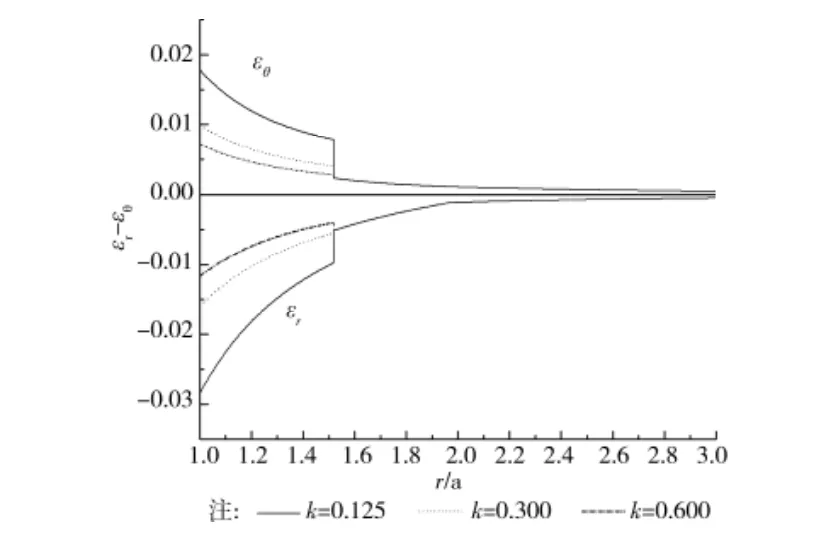
图4 弹模劣化系数k对围岩应变的影响

5 结 论

1）在理想弹脆性模型的基础上，加上一个软化阈值，建立了弹塑脆性模型，研究岩土开挖中的硐室围岩弹塑性问题，基于M－C强度理论和非关联流动法则，得到了圆形硐室围岩应力与变形解析表达式。

2）软化阈值变化对围岩应力场影响显著，随着软化阈值的增大，塑性区围岩应力增大，变形减小，反之亦然。

3）分析了岩石弹模劣化系数对围岩变形的影响。随着劣化程度的加大，破裂区范围变化不大，围岩变形显著，是地下工程近巷围岩大变形的重要原因。

［1］周宏伟，谢和平，左建平.深部高地应力下岩石力学行为研究进展［J］.力学进展，2005，35（1）：91－99.Zhou H W，Xie H P，Zuo J P.Developments in researches on mechanical behaviors of rocks under the condition of high ground pressure in the depths ［J］.Advances in Mechanics，2005，35（1）：91－99.

［2］王德荣，甄树新，汪新红，等.深部坑道围岩压力与变形分析［J］.岩土力学，2007，28（3）：70－77.Wang D R，Zhen S X，Wang X H，et al.Analysis of pressure and deformation of wall rock near deep tunnel［J］.Rock and Soil Mechanics，2007，28（3）：70－77.

［3］刘泉声，卢兴利.煤矿深部巷道破裂围岩非线性大变形及支护对策研究［J］.岩土力学，2010，31（10）：3273－3280.Liu Q S，Lu X L.Research on nonlinear large deformation and support measures for broken surrounding rocks of deep coal mine roadway［J］.Rock and Soil Mechanics，2010，31（10）：3273－3280.

［4］张黎明，王在泉，李华峰，等.粉砂岩峰后破坏区应力脆性跌落的试验和本构方程研究［J］.实验力学，2008，23（3）：234－240.Zhang L M，Wang Z Q，Li H F，et al.Theoretical and experimental study on siltstone brittle stress drop in post failure region ［J］.Journal of Experimental Mechanics，2008，23（3）：234－240.

［5］王水林，王威，吴振君.岩土材料峰值后区强度参数演化与应力－应变曲线关系研究［J］.岩石力学与工程学报，2010，29（8）：1524－1529.Wang S L，Wang W，Wu Z J.Study of relationship between evolution of post－peak strength parameters and stress－strain curves of geomaterlals［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29（8）：1524－1529.

［6］Hoek E，Brown T E.Practical estimates of rock mass strength ［J］.International Journal of Rock Mechanics and Mining Sciences，1997，34（8）：1165－1186.

［7］Sharan K S.Eastic－brittle－plastic analysis of circular openings in Hoek－Brown media ［J］.International Journal of Rock Mechanics and Mining Sciences，2003，40（6）：817－824.

［8］Lee K Y，Pietruszczak S.A new numerical procedure for elasto－plastic analysis of a circular opening excavated in a strain－softening rock mass ［J］.Tunnelling and Underground Space Technology，2008，23（5）：588－599.

［9］Carranza T C，Fairhurst C.The elasto－plastic response of underground excavations in rock masses that satisfy the Hoek－Brown failure criterion ［J］.International Journal of Rock Mechanics and Mining Sciences，1999，36（6）：777－809.

［10］Chandra S，Nilsen B，Ming L.Predicting excavation methods and rock support：a case study from the Himalayan region of India［J］.Bulletin of Engineering Geology and the Environment，2009，69（2）：257－266.

［11］潘岳，王志强.基于应变非线性软化的圆形硐室围岩弹塑性分析［J］.岩石力学与工程学报，2005，24（6）：915－921.Pan Y， Wang Z Q.Elasto－plastic analysis on surrounding rock of circular chamber based on strainnonlinear softening ［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（6）：915－921.

［12］王亮，赵均海，李小伟.岩质圆形隧洞围岩应力场弹塑性新解［J］.工程地质学报，2007，15（3）：424－428.Wang L，Zhao J H，Li X W.New elasto－plastic solution of rock circular tunnel surrounding rockmass stress field［J］.Journal of Engineering Geology，2007，15（3）：424－428.

［13］蒋斌松，张强，贺永年，等.深部圆形巷道破裂围岩的弹塑性分析［J］.岩石力学与工程学报，2007，26（5）：983－986.Jiang B S，Zhang Q，He Y N，et al.Elastoplastic analysis of cracked surrounding rocks in deep circular openings［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26（5）：983－986.

［14］范文，俞茂宏，陈立伟，等.考虑剪胀及软化的洞室围岩弹塑性分析的统一解［J］.岩石力学与工程学报，2004，23（19）：3213－3221.Fan W，Yu M H，Chen L W，et al.Unified elastoplastic solution for surrounding rocks of openings with consideration of material dilatancy and softening ［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23（19）：3213－3221.

［15］李同录，陈立伟，俞茂宏，等.考虑材料软化的洞室围岩弹塑性分析的统一解［J］.长安大学学报：自然科学版，2004，24（3）：49－52.Li T L，Chen L W，Yu M H，et al.Unified solution of elastic－plastic surrounding rocks of cavity considering material softening［J］.Journal of Chang'an University：Natural Science Edition，2004，24（3）：49－52.

［16］张常光，胡云世，赵均海，等.深埋圆形水工隧洞弹塑性应力和位移统一解［J］.岩土工程学报，2010，32（11）：1738－1746.Zhang C G，Hu Y S，Zhao J H，et al.Elastic－plastic unified solutions for stresses and displacements of a deep buried circular hydraulic tunnel ［J］.Chinese Journal of Geotechnical Engineering，2010，32（11）：1738－1746.

［17］江权.高地应力下硬岩弹脆塑性劣化本构模型与大型地下洞室群围岩稳定性分析［D］.武汉：中国科学院武汉岩土力学研究所，2007.