基于双端队列的类Josephus逆问题求解

李胜华,赵晗诺

(湖北大学数学与计算机科学学院,湖北 武汉 430062)

0 引言

一种扑克牌游戏:取A～K 13张扑克牌叠在一起,从上面拿一张放在最下面,再从上面拿一张出来显示,重复此操作,要求显示出来的顺序是:A、2、3、4、……、J、Q、K.据说著名犹太历史学家Josephus有过以下的故事:在罗马人占领乔塔帕特后,39个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式:41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止.然而Josephus和他的朋友并不想遵从,Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏.后人将此游戏推广成(n,m,k)-Josephus问题[1]:设有n个人围成一个圆圈,并依次编号为1,2,…,n.要求从编号为k的那个人开始从1报数,顺序报数到m的人出列,然后从出列的下一个人重新开始从1报数,顺序报数到m的人又出列,此过程重复直到所有的人都出列(或只剩下一个人)为止.对于任意给定的自然数n,m和k,试给出这n个人的出列次序(或最后出队者的编号).

对于上述的扑克牌游戏,聪明的看客看了几遍,或记下初始顺序或推理一番也会演示了,但很少从理论上研究.毋庸置疑,参加Josephus游戏的现代人都想做Josephus,使自己最后出局.这其实是Josephus逆问题:已知n、m、k及n个人的出列次序,求原始排列顺序.对于Josephus问题,文献[2-5]对其有较深入的研究,他们主要是基于循环顺序表和循环链表两大类实现方法.然而,这两类实现方法对于Josephus逆问题求解不方便.

本文中首先对扑克牌游戏及Josephus逆问题进行推广得到类Josephus逆问题,然后探讨适合此类问题求解的数据结构及算法.

1 问题的定义

分析(n,m,k)-Josephus问题,可知是对一批数据按照规定的操作规则进行删除,每次删除一个数据.实际应用中,可以将其推广为每次删除多个数据.下面给出基于操作的类Josephus问题的定义:

1.1类Josephus问题对类型相同依次排列的n个数据,先进行k次1个数据从前面移至后面的操作,然后重复进行下面两种操作:

1)m次将1个数据从前面移至后面;

2)从前面顺序取s个数据出列.

直至数据全部出列,求这n个数据的出列次序.

显然当s=1时,类Josephus问题即是(n,m,k)-Josephus问题.对于类Josephus问题用文献[2-5]的方法同样可求解.引言中的扑克牌游戏及Josephus逆问题本质上是一个已知操作过程及操作结果,求初始状态的问题,为此定义上述问题的逆问题:

1.2类Josephus逆问题对类型相同依次排列的n个数据,进行与类Josephus问题相同的操作,已知这n个数据的出列次序,求它们的原始顺序.

下面列举一些类Josephus逆问题的实例:

例1 引言中的扑克牌游戏:已知n=13,k=0,m=1,s=1,对A～K 13张牌进行类Josephus问题中的操作,要求出列次序为A、2、3、4、…、J、Q、K,求扑克牌的原始顺序.

例2 Josephus考虑的问题:已知n=41,k=0,m=2,s=1,对编号1～n的人进行类Josephus问题中的操作,出列顺序要求Josephus和他的朋友在最后两个,求Josephus和他的朋友的原始号码.

由类Josephus逆问题也产生了一类扑克牌游戏:

例3 A、3、5、7、9各两张,2、4、6、8、10各一张共15张扑克牌叠在一起,每次从上面拿牌到下面2次,再从上面出牌2次,要求牌出来的顺序为A、A、2、3、3、4、5、5、6、7、7、8、9、9、10.求扑克牌的原始顺序.这也是n=15,k=0,m=2,s=2的类Josephus逆问题.

类Josephus逆问题是已知操作过程及操作结果,求操作初态,很容易想到用倒推法求解:在操作结果的基础上进行逆向操作得出数据的初始状态.为了验证解的正确性,可以利用类Josephus逆问题的解再做类Josephus问题.用计算机求解问题需要选择合适的数据结构来存储这些数据,考虑操作只涉及到前面和后面数据的处理,求解过程的逆操作也只是前面和后面数据的处理,故队列应是表示前述问题中的数据最合适的数据结构.

队列是一种插入和删除操作受限的线性表,它的插入和删除只能在两端进行.如果只能在一端插入,另一端删除的队列称先进先出队列;如果删除按元素的优先级来删除的队列称优先队列.这两种队列应用较广泛,讨论较多[6-7].上述问题中的操作是在前面删除,后面插入;求解过程中的逆操作是在下面插入,上面删除.因而求解类Josephus逆问题及验证解需要队列的两端都能插入和删除,这种队列叫双端队列.我们将基于双端队列的存储,讨论类Josephus逆问题的计算机求解及解的验证.

2 双端队列

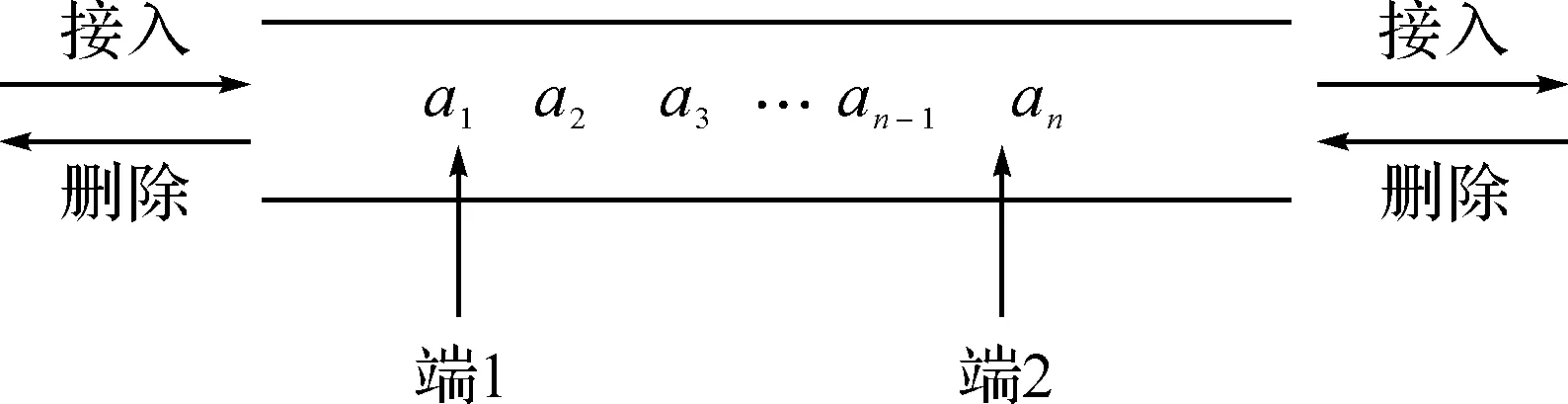
图1 双端队列

图2 铁道转轨网

双端队列是限定插入和删除操作在表的两端进行的线性表,示意图见图1,也可用图2的铁道转轨网络形象描述双端队列.本节中首先给出双端队列的抽象数据类型定义,然后讨论双端队列的顺序循环实现.

线性表是多个相同类型的数据元素的集合,且这些元素间具有线性关系.双端队列是只能在两端进行插入和删除的线性表,常用的基本操作有插入、删除、判断队列是否为空、判断队列是否满等.由于具体应用中的队列两端操作的限制不一样,它的定义和实现略有区别.文献[8-9]中的双端队列是基于先进先出队列及先进后出栈实现的.下面给出队列两端都能进行插入和删除的抽象数据类型双端队列的定义.

ADT DEQueue{

数据对象:D={ai| ai∈ElemSet, i=1, 2, …, n, n≥0}.

数据关系:R={| ai∈ D , i=2, …, n}约定a1为端1元素,an为端2元素.

基本操作:

InitDEQueue(&Q); //构造一个空双端队列

ClearDEQueue(&Q); //双端队列Q存在,清空它

DEQueueEmpty(Q); //双端队列Q存在,判断它是否为空

DEQueueFull(Q); //双端队列Q存在,判断它是否满

EnDEQueue1(&Q, e); //双端队列Q存在,在端1插入元素e

EnDEQueue2(&Q, e); //双端队列Q存在,在端2插入元素e

DeDEQueue1(&Q, &e); //双端队列Q存在,删除端1元素,用e返回其值

DeDEQueue2(&Q, &e); //双端队列Q存在,删除端2元素,用e返回其值

Get1(Q, &e); //双端队列Q存在,用e返回端1元素的值

Get2(Q, &e); //双端队列Q存在,用e返回端2元素的值

OutputDEQueue(Q); //依次输出双端队列中从端1到端2的元素

} ADT DEQueue

双端队列的实现一般可分为链式和顺序两大类.文献[10]中的双端队列是基于双链表的实现.由于队列操作只在两端,如果能预估数据元素个数的最大值,用顺序存储可以简化操作,本文中实现的方式是顺序方式.双端队列的顺序存储是用一组地址连续的存储单元依次存放从端1到端2的元素,同时附设两个指针end1和end2分别指示端1元素和端2元素的位置.由于队列两端可随时插入、删除元素,end1和end2会动态变化,为提高存储率,元素的存储空间可当成环形空间使用,即最后一个单元的下一个存储单元是第一个单元,此时队列称为顺序循环双端队列.我们约定:初始化队列时,申请一个QUEUE_MAX_SIZE(足够用)大小的空间,end1=end2=0;每当在端1插入、删除元素,end1对应减1、增1;每当在端2插入、删除元素,end2对应增1、减1.因此,当双端队列非空时,end1总是指向端1元素,end2总是指向端2元素的下一个位置.为了区分队空队、队满,本文中还约定存储空间要空一个单元不用.这样,当end1= =end2时,双端队列为空;当(end2+1) = =end1,双端队列为满.这里的增、减是基于模QUEUE_MAX_SIZE意义上的.假设双端队列数据元素的类型为ElemType,下面给出顺序循环双端队列的存储结构:

const QUEUE_MAX_SIZE=100; //存储空间的大小

typedef struct {

ElemType *base; //元素存放首地址

int end1, end2; //指示队列的两端

} DESQueue; //顺序循环双端队列

typedef DESQueue DEQueue;

抽象数据类型双端队列定义中的相关操作的实现,见附录.

3 问题的求解、验证及算法分析

约定第2节定义中的数据用顺序循环队列存储,前面为端1,后面为端2.求解类Josephus逆问题的基本思想是借助一个空双端队列,用类Josephus逆问题中的元素的出队序列按逆序进行如下操作:首先重复进行后两种操作,1)从端1顺序插入s个数据,2)m次将1个数据从端2移至端1,最后进行k次1个数据从端2移至端1操作.操作结束,双端队列从端1到端2的数据就是n个数据的原始序列,即为类Josephus逆问题的解.利用双端队列将此原始序列进行规定的操作可得到出队序列,从而模拟和验证.注意到数据元素一共有n个,端1连续删除元素s次,当s不整除n时,则最后一次只能连续删除n(mods)次.因此,求解过程中操作的第一次从端1插入及演示操作时的最后一次从端1删除要单独处理.下面是分别是求解类Josephus逆问题及类Josephus问题的算法.

3.1算法1void ProblemSolving(ElemType A[ ], int n, int m, int k, int s){

// A存放n份数据(按出队顺序的逆序),进行类Josephus问题中的逆操作,输出初始序列

InitDEQueue (Q) //初始化双端队列Q

p=0;

//处理特殊的第一组

if(n%s){

for(i=1; i<=n%s; i++)EnDEQueue1(Q, A[p++]); //数据依次从端1插入

for(j=1; j<=m; j++){// 从端2删除一元素,将该元素再从端1插入

DeDEQueue2(Q, temp); EnDEQueue1(Q, temp);

}

}//if

while(p

for(i=1; i<=s; i++) EnDEQueue1(Q, A[p++]);

for(j=1; j<=m; j++){

DeDEQueue2(Q, temp); EnDEQueue1(Q, temp);

}

}//_while

for(i=1; i<=k; i++){//

DeDEQueue2(Q, temp); EnDEQueue1(Q, temp);

}

OutputDEQueue(Q); //输出队列各元素,即类Josephus逆问题的解

}//end

3.2算法2void ProblemProving(DEQueue &Q, int n, int m, int k, int s){

//Q中存放类Josephus逆问题的解,进行规定的操作,输出出队序列

for(i=1; i<=k; i++){// 从端1删除一元素,将该元素再从端2插入

DeDEQueue1(Q, temp); EnDEQueue2(Q, temp);

}

for(i=1; i<=n/s; i++){

for(j=1; j<=m; j++){

DeDEQueue1(Q, temp); EnDEQueue2(Q, temp);

}

for(j=1; j<=s; i++){// 从端1删除元素

DeDEQueue1(Q, temp); cout<

}

}//_for

// 处理最后一组数据

if(n%s){

for(j=1; j<=m; j++){

DeDEQueue1(Q, temp); EnDEQueue2(Q, temp);

}

while(!DEQueueEmpty(Q)){

DeDEQueue1(Q, temp); cout<

}

}//if

}//_end

利用算法1,可求得例1中扑克牌的原始顺序从上至下应依次为7、A、Q、2、8、3、J、4、9、5、K、6、10;例2中Josephus和他的朋友的原始号码为31和16;例3中扑克牌的原始顺序从上至下应依次为5、8、A、A、9、6、2、3、7、10、3、4、9、7、5.利用算法2很容易验证它们的正确性.

下面简单地分析上述两个算法的效率.两个算法中主要的存储空间是一个队列,队列的大小为元素的个数,所以空间复杂性为Ο(n).两个算法中的主要操作是元素进队、出队,操作总次数相等,用T(n,m,k,s)表示算法1、算法2中进队、出队总的操作次数,即时间复杂性.由上述算法易知,

4 结论

本文中定义了类Josephus逆问题,探讨了这类问题的求解.实验表明:双端队列是求解类Josephus逆问题及验证解的正确性的一种很好的数据存储结构.下一阶段的工作将探讨算法的改进及类Josephus逆问题的应用.

5 附录:双端队列的顺序循环实现

下面给出与本文中有关的双端队列顺序循环实现算法,包括双端队列的初始化、两个出队、两个入队及一个输出算法.

int InitDEQueue(DEQueue Q){

Q.base= new ElemType[QUEUE_MAX_SIZE];

if(!Q.base)return 0; // 空间不够,返回失败标志

Q.endl=Q.end2=0;//end1和end2都指示起始位置

return 1; //成功

}

int EnDEQueue1(DEQueue &Q, ElemType e){//从端1入队

if(DEQueueFull(Q)) return 0; //空间不够,失败

Q.end1=(Q.end1+QUEUE_MAX_SIZE-1)%QUEUE_MAX_SIZE;

Q.base[Q.end1]=e;

return 1;

}

int EnDEQueue2(DEQueue &Q, ElemType e){//从端2入队

if(DEQueueFull(Q)) return 0; //空间不够,失败

Q.base[Q.end2]=e;

Q.end2=(Q.end2+1)% QUEUE_MAX_SIZE;

return 1;

}

int DeDEQueue1(DEQueue &Q, ElemType &e){//从端1出队

if(DEQueueEmpty(Q)) return 0;//空队列,失败

e=Q.base[Q.end1];

Q.end1=(Q.end1+1)%QUEUE_MAX_SIZE;

return 1;

}

int DeDEQueue2(DEQueue &Q, ElemType &e){//从端2出队

if(DEQueueEmpty(Q)) return 0;//空队列,失败

Q.end2=(Q.end2+QUEUE_MAX_SIZE-1)%QUEUE_MAX_SIZE;

e=Q.base[Q.end2];

return 1;

}

void OutputDEQueue(DEQueue Q){ //输出队列元素,约定从队头到队尾

if(DEQueueEmpty(Q)) {cout<<″空队列！！！″; return;}

i=Q.end1;

do{

cout<

i=(i+1)% QUEUE_MAX_SIZE;

}while(i!=Q.end2);

}

[1] Graham R L, Knuth D E, Patashnik O.具体数学[M].庄心谷,译.西安:西安电子科技大学出版社,1992.

[2] Gregory L W, Christopher L M. An application of Fourier transforms on finite Abelian groups to an enumeration arising from the Josephus problem[J]. Journal of Number Theory,2010,130:815-827.

[3] Ruskey F, Williams A. The feline josephus problem[J]. Theory Comput Syst,2012,50:20-34.

[4] 王永红.约瑟夫环经典问题的几种算法比较[J].现代计算机,2008,(1):36-37.

[5] 陈海山,钱锋,田英,等.Josephus问题的算法设计与应用研究[J].计算机工程与应用,2007,43(1):61-64.

[6] 严蔚敏,吴伟民.数据结构[M].北京:清华大学出版社,2002.

[7] 王晓东.计算机算法设计与分析[M].第3版.北京:电子工业出版社,2007.

[8] 陈佳娟,王云鹏,纪寿文.配送实时调度管理系统中最短路径的双队列算法及其JAVA实现[J].计算机工程与应用,2004,33:227-229,232.

[9] 陈洁,陆锋.一种基于双端队列的交通网络最短路径Pallottino优化算法[J].中国图象图形学报,2006,11(3):419-424

[10] 杨东升,张连法.改进型锁无关双端队列的设计与实现[J].计算机系统应用,2012,21(3):125-129.