基于类桁架材料模型优化方法计算稳定性研究

李霞,周克民

(华侨大学土木工程学院,福建 厦门 361021)

0 引言

在结构优化领域,Michell的理论具有里程碑的意义[1],不仅揭示了优化结构的类桁架性质,而且一直作为检验其它方法的可靠依据.但是Michell理论采用解析方法求解困难,得到的拓扑优化结构是非均匀各向异性连续体,并非工程意义上的桁架,难以在工程实际中应用.随着计算机技术、有限元方法和数学优化理论的发展,结构拓扑优化研究取得了许多重要进展,主要集中在基于有限元的数值方法.人们试图通过在等厚板中寻找孔的优化分布实现拓扑优化,包括均匀化方法[2],进化结构优化方法[3],水平集方法[4]和ICM方法[5]等.为了得到等厚板,普遍需要抑制中间密度,抑制中间密度直接导致了单元铰接,棋盘格现象、单元依赖性等数值不稳定问题[6-7].虽然自由材料优化方法不存在数值不稳定问题,但优化结果缺乏与实际结构的明确对应关系[8-9].

按照Michell理论,拓扑优化结构一般是由无限多致密杆件构成的非均匀各向异性连续体,各种拓扑优化数值方法试图用均匀等厚带孔板逼近这种非均匀各向异性连续体.在有限元理论的基本假设下,这种黑白相间的“棋盘格”状态是很好的近似.随着单元网格的增加,拓扑描述清晰度的提高,出现更多的细部结构,出现优化结果的网格依赖性.因此,出现这些数值不稳定问题是必然的.目前也有一些方法,如周长控制、梯度控制等可以避免或减轻这些现象.理论上的拓扑优化结构是各向异性连续体,实际需要均匀等厚带孔板,这两者之间的矛盾是出现这些问题的根本原因.

本作者曾提出基于类桁架材料模型的拓扑优化方法[10],试图通过优化类桁架材料的分布场实现结构的拓扑优化,而不是直接优化等厚板中孔的分布.采用有限元的数值分析方法构造设计域内杆件非均匀连续分布场,从而直接找到理论上的最优结构-Michell桁架.由于不抑制中间密度,所以完全没有数值不稳定问题.为了满足工程实际需要,再将类桁架连续体转化为离散结构.一些算例表明这种离散的误差不大[11-12].本文中目的在于分析该方法的稳定性,即对有限元网格的无关性以及棋盘格现象等,这是传统方法普遍存在的问题[13].

1 类桁架材料模型

为了构造类桁架连续体结构,首先建立类桁架连续体材料模型.假设在弱的基材料内非均匀连续分布致密的杆件,杆件的分布密度和方向在设计域内连续变化.基材料不受力,力完全由分布杆件承担.优化的目的是建立这种杆件分布场.对于本文中研究的单工况应力约束体积最小问题,假设杆件在任意点沿两个正交方向分布杆件.该问题是最经典的结构拓扑优化问题,经常作为验证各种拓扑优化方法的标准算例,其优化结果常称为Michell桁架.

1.1 弹性矩阵

σi=Etiεi,i=1,2

(1)

在单工况下,考虑到类桁架材料中相邻平行杆件之间没有相互作用,所以横向变形系数和剪切刚度均为零.为了避免结构刚度矩阵奇异,假设切应力τ12和切应变γ12之间的关系为,

τ12=E(t1+t2)γ12/4

(2)

如此假设条件下,该材料模型当t1=t2时可以表示各向同性材料.实际上在优化结构中,由于主应力沿材料主轴方向,所以材料主方向无切应变,剪切刚度不起作用.因此,材料主轴方向的应力应变的可以表示为

[σ1σ2τ12]=D(t1,t2,0)[ε1ε2γ12]

(3)

式中D(t1,t2,0)是材料主轴方向的弹性矩阵,D(t1,t2,0)=E·diag[t1t2(t1+t2)/4]

(4)

diag表示对角矩阵.

在多工况下,杆件一般不正交,也存在切应变.作为一种近似,本文中仍采用了以上假设.

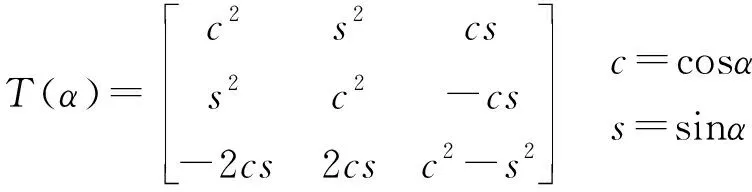
除对申请书进行评审之外，二审专家组的另一任务是在评审结束后将各领域的相对资助率进行综合，平衡各研究领域的资助力度。

(5)

可以建立结构坐标系下的弹性矩阵D(t1,t2,α)=TT(α)D(t1,t2,0)T(α)

(6)

为了简单具体写出式(6),定义几个常数矩阵,

(7)

和函数矩阵

g(α)=[cos2αsin2α1]

(8)

(9)

式中sbr和gr分别是式(7)和式(8)定义矩阵的分量.

1.2刚度矩阵如果杆件在结点j位置的密度和方向分别为t1j,t2j和αj,弹性矩阵记作D(t1j,t2j,αj),单元内任意点(ξ,η)的弹性矩阵De(ξ,η)可以通过形函数Nj(ξ,η)插值计算

(10)

式中Se为属于单元e的结点集合.定义与材料分布无关的常数矩阵

(11)

(12)

2 优化方法

以杆件在结点位置的密度和方向t1j,t2j,αj(j=1,2,…,J)为优化设计变量,单元内部任意点的杆件密度由结点位置的杆件密度插值得到.将杆件密度在设计域内积分得到结构体积

(13)

式中Sj是围绕结点j的单元集合,J是结点总数,zj是形函数在围绕结点j的单元内杆件体积积分之和

(14)

式中Ve是单元面积.本文中研究应力约束体积最小问题

(15)

式中l表示工况,L为工况总数,σp为允许应力.

2.1单工况优化采用满应力准则法优化杆件在结点位置的密度

(16)

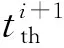
2.2多工况优化多工况下仍假设优化结构中任意点有两个方向的正交杆件.首先在各单工况下分别得到杆件优化分布t1l,t2l,αl.按照坐标变换的概念可以写出任意方向的刚度矩阵

D(φ;t1l,t2l,αl)=D(t1l,t2l,φ-αl),

(17)

取对角元第1行第1列的元素为度量基础,定义为方向刚度,各工况下方向刚度的包络线方程为

(18)

多工况下任意点位置的杆件密度和方向记作x1,x2,θ,定义多工况下方向刚度与各单工况下方向刚度的包络线的差值为

(19)

假设多工况下的优化结构与各单工况下的方向最大刚度差值最小,即取住值

(20)

可以解得多工况下杆件密度和方向角

x1+x2=2I0x1-x2=4(I1sin2θ+I2cos2θ), tan2θ=I1/I2

(21)

(22)

3 数值算例

下面通过简支结构、悬臂结构、多工况3个经典算例分析不同网络划分，即不同单元密度对优化结果的影响.由于问题与量纲无关，这里的所有数据均无量纲，力和弹性模量均取1.图1是矩形域下边两端简支，中点作用竖向集中力的简支结构，图2(a)、图2(b)是简支结构采用2种不同的4结点矩形规则单元密度的优化结果，图2(c)是解析解[14].图3是矩形域左边固定，右边中点作用竖向集中力的悬臂结构，图4(a)、图4(b)、图4(c)是悬臂结构采用3种不同的规则单元密度的优化结果，图4(d)是解析解[15].图5是悬臂结构采用2种不同的不规则单元的优化结果.图6是2个力分别作用在右边上下2个角点的多工况，图7是多工况采用2种不同的规则单元密度的优化结果.表1给出了优化结构所使用的材料体积及迭代次数.

表1 单元数量及优化结果

图1 简支结构

图2 简支结构不同密度规则单元的优化结果(a)20×12;(b)40×24;(c)解析解.

图3 悬臂结构

图4 悬臂结构不同密度规则单元的优化结果(a)10×16;(b)20×32;(c)40×64;(d)解析解.

图5 悬臂结构不同的不规则单元的优化结果(a)10×16;(b)10×16.

图6 多工况结构

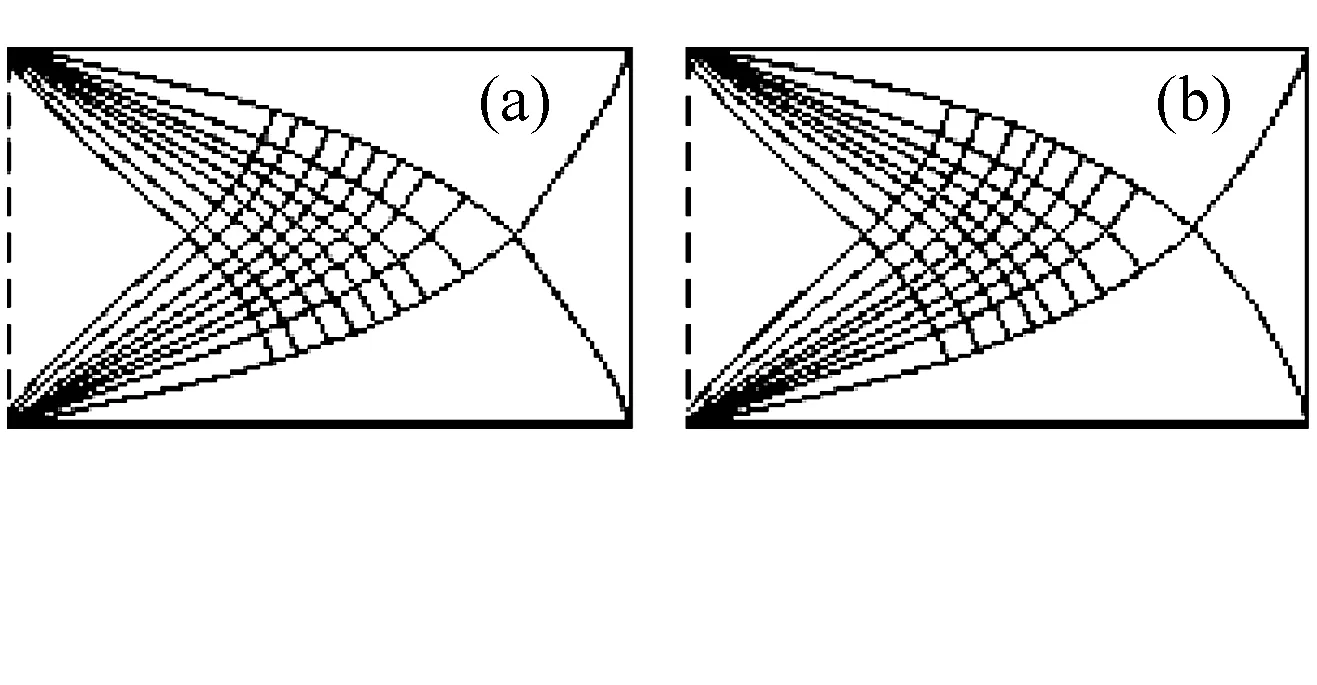
图7 多工况不同密度规则单元的优化结果(a)20×32;(b)40×64.

比较这些优化结果可以看出,其数据均非常接近,单元网格的密度和形状对优化结果影响很小.所有算例均未出现数值不稳定问题,验证了基于类桁架连续体材料模型优化方法数值计算结果的稳定性.

4 结语

数值不稳定问题是各种数值拓扑优化方法普遍存在的问题,虽然可以采取一些方法减轻这种问题,但不可能完全解决,且增加了计算量.基于类桁架连续体材料模型的拓扑优化方法没有单元铰接、棋盘格现象,其结果受网格划分影响很小.

[1] Michell A. The limits of economy of material in frame structure[J]. Phil Mag,1904,8(6):589-597.

[2] Bendsoe M, Kikuchi N. Generating optimal topologies in structural design using a homogenization method[J]. Comput Methods Appl Mech Engrg,1988,71(2):19-224.

[3] Querin O M, Young V, Steven G P, et al. Computational efficiency and validation of bi-directional evolutionary structural optimization[J]. Comput Methods Appl Mech Engrg,2000,189(2):559-573.

[4] Sethian J, Wiegmann A. Structural boundary design via level set and immersed interface methods[J]. J Comput Phys,1999,163:489-528.

[5] Sui Y, Yang D. A new method for structural topological optimization based on the concept of independent continuous variables and smooth model[J]. Acta Mechanica Sinica,1998,14(2):179-185.

[6] Sigmund O, Petersson J. Numerical instabilities in topology optimization: a survey on procedures dealing with checkerboards, mesh-dependencies and local minima[J]. Struct Optim,1998,16(1):68-75.

[7] Cheng K, Olhoff N. An investigation concerning optimal design of solid elastic plates[J]. Int J Solids Structures,1981,17(3):305-323.

[8] Matsui K, Terada K. Continuous approximation of material distribution for topology optimization[J]. Int J Numer Meth Engng,2004,59(4):1925-1944.

[9] Bendsoe M, Sigmund O. Material interpolations in topology optimization[J]. Arch Appl Mech,1999,69(9-10):635-654.

[10] Zhou K, Li X. Topology optimization of structures under multiple load cases using fiber-reinforced composite material model[J]. Comput Mech,2005,38(2):163-170.

[11] Zhou K, Li J. The exact weight of discretized michell trusses for a central point load[J]. Struct Optim,2004,28(1):69-72.

[12] Prager W. A note on discretized michell structures[J]. Comput Methods Appl Mech Eng,1974(3):349-355.

[13] Eschenauer H, Olhoff N. Topology optimization of continuum structures: a review[J]. Applied Mechanics Reviews,2001,54(4):331-389.

[14] Hemp W. Optimum structure[M]. Oxford, Clarendon Press,1973.

[15] Lewinski T, Zhou M, Rozvany G. Extended exact solutions for least-weight truss layouts — paper Ⅰ: cantilever with a horizontal axis of symmetry[J]. Int J Mech Sci,1994,36(5):375-398.