具有矩阵值的广义正交周期小波包
毛一波
(重庆文理学院数学与财经学院,重庆 永川 402160)
0 引言及预备知识
由于小波包能够解决单一正交小波基的频域局部化较差的问题而成为小波分析的研究热点,它在信号处理、图象压缩、编码理论、通信工程等方面有诸多应用[1-2].Coifman等[3]首先引入了一元正交小波包的概念;Xia等[4]引入矩阵值小波的概念,研究了矩阵值正交小波的存在性及其构造;陈清江等[5]将小波包的概念推广到矩阵值正交小波包情形;彭思龙、李登峰[6]将小波概念引入到周期函数空间,建立了周期小波理论;我们在文献[7]中则将实直线上的小波包推广到正交周期小波包,建立了其理论框架并研究了其性质.在上述理论的基础上,将小波包进行推广,引入一类矩阵值广义正交周期小波包,并研究其性质,建立其分解公式和频域表示公式.
考虑周期为1的s×r矩阵值函数空间S,其中S定义为:
S:=L2([0,1),Cs×r):={F(t):=(fk,l(t))s×r|fk,l(t)=fk,l(t+1),
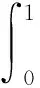
对F(t),G(t)∈S,F(t)的积分为如下的s×r矩阵:
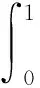
1 矩阵值周期多分辨分析
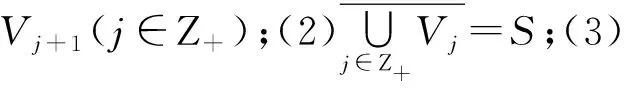
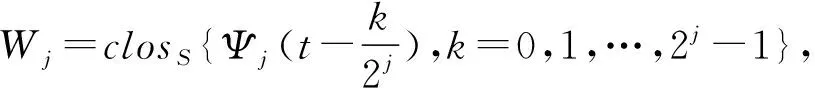
(1)
(2)

(3)
成立(其中θ为零矩阵).

其余两式同理可证,从略.
2 矩阵值广义正交周期小波包

(4)

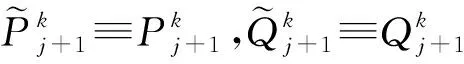
3 主要结果

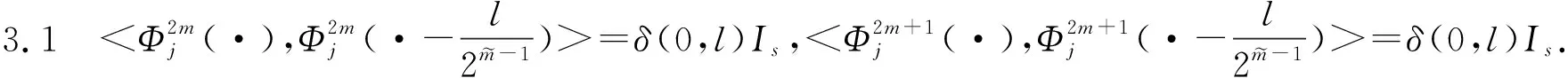
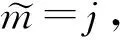

不妨设当m m0=2m1+λ1,m1=2m2+λ2,…,mτ-1=2mτ+λτ,…, 性质3.4的证明由m的分解表示及小波包定义知 通过对正交周期小波包概念的推广,引入了一类具有矩阵值的广义正交周期小波包,并给出了具有矩阵值的广义正交周期小波包的构造方法.通过具有矩阵值的广义正交周期小波包的构造,可以对正交周期小波子空间Wj进行正交分解,最终可以分解为2j个一维小波子空间的正交直和.通过对具有矩阵值的广义正交周期小波包的性质进行研究,得到了具有矩阵值的广义正交周期小波包的分解公式及其Fourier变换表示,推广了正交周期小波包和向量值小波包的结果. [1] 田秀荣.基于正交小波包分解的语音去噪增强[J].计算机仿真,2011(5):388-390. [2] 郭业才,纪娟娟.基于正交小波包变换的变步长双模式盲均衡算法[J].系统仿真学报,2011(2):335-338. [3] Coifman R, Meyer Y, Wickerhauser M V.Size properties of wavelet packets//Ruskai M B, Beylkin G, Coifman R, et al. Wavelets and Their Applications[M]. New York: Academic Press, 1992:153-178. [4] Xia X G,Suter B W.Vector-valued wavelets and vector fiter banks[J]. IEEE Trans Signal Processing,1996,44:508-518. [5] 陈清江,张同琦,程正兴.一类矩阵值小波包的刻划[J].兰州理工大学学报,2006(2):143-146. [6] 彭思龙,李登峰,陈翰麟.周期小波理论及其应用[M].北京:科学出版社,2003. [7] 毛一波.正交周期小波包[J].湖北大学学报:自然科学版,2011(1):22-24.
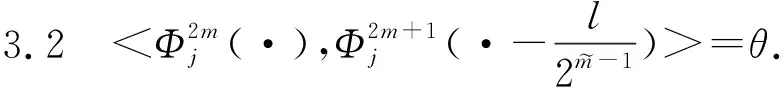
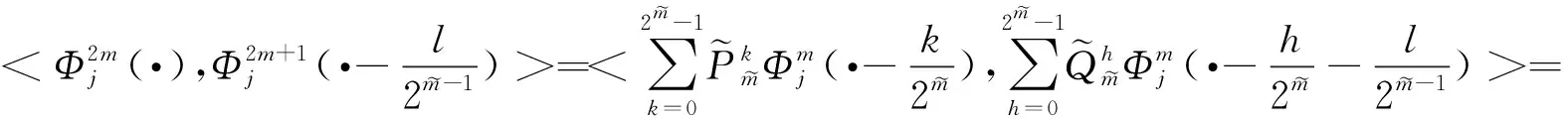


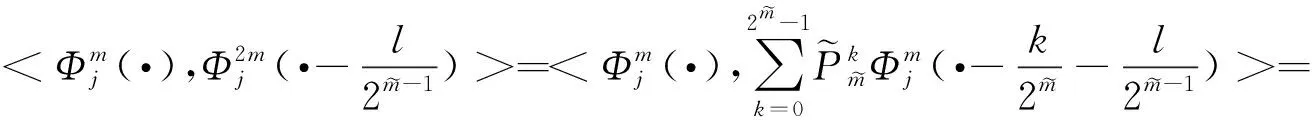
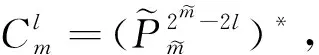

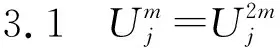


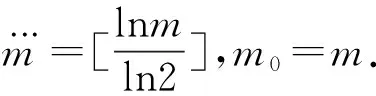
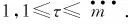


4 结论

