基于可拓评价方法的运动员竞技能力状态诊断——以羽毛球优秀运动员为例
卓建南,尹少丰
(1.广东工业大学 体育部,广东 广州 510090;2.南华工商学院 体艺部,广东 广州 510507)
竞技能力是指运动员进行训练和参加比赛所具备的专门能力。以能力而论,竞技能力主要由体能、技能、战术能力、心理能力4种基本能力所构成[1]。运动员竞技能力状态诊断是指在训练过程中的特定时刻,对运动员竞技能力及其训练状况的检查和评定。运动员竞技能力状态诊断对制定训练目标、组织训练活动和实施有效的训练调控都起着非常重要的作用[2]。
羽毛球运动是我国竞技体育中的优势项目,特别是在我国羽毛球运动蓬勃发展的当前,寻求羽毛球运动员竞技状态诊断的科学化方法,并以此为依据制定科学的训练计划,实现运动训练过程的最优化,成为了广大羽毛球教练员和科研人员共同关注的焦点。现阶段,我国羽毛球运动员竞技状态诊断,特别是基层运动队的运动员竞技状态诊断,还主要是由教练员或教练组在运动员训练指标测试分析的基层上,依据经验进行的评定过程。这种以经验为依据的定性诊断,往往只能顾及到单一指标本身,很难考虑到指标体系的整体和各指标之间的相互联系,因此往往无法取得准确的诊断效果。鉴于此,本研究引入可拓评价方法,建立了可以综合考察优秀羽毛球运动员训练指标体系的竞技能力状态诊断可拓物元模型,以期为科学诊断我国优秀羽毛球运动员竞技状态提供参考。
可拓方法是我国学者蔡文[3]创建的一种全新的系统分析方法。它借助于物元理论和可拓数学,以探讨矛盾问题的解决方法为切入点,通过物元的可拓性进行发散性思维,利用物元变换寻找解决问题的各种方法,因而能充分考虑到事物的各个方面,得到整体的系统分析效果。
事物N具有特征c,其值为v,则由(N,c,v)构成有序的三元组R=( N,c,v)作为描述事物的基本元,简称物元。事物的名称N,特征c和量值 v,称为物元R的三要素。物元概念可将客观世界比拟为一个相互联系的物元网络,一个物元的变换会导致相关物元的变换,从而传导到与之相关的另外一系列物元中去。在实际应用中,我们可以通过建立事物运行状态的物元模型,再利用关联函数计算出该事物运行状态各等级之间的关联度,最终达到识别该事物运行状态的目的[4]。
1 优秀羽毛球运动员竞技能力状态诊断的可拓评价方法
1.1 优秀羽毛球运动员竞技能力状态诊断物元
优秀运动员的竞技状态是个复杂的系统,由于受到运动员生理、心理、训练环境等各方面因素的影响,会出现不同程度的起伏[5]。因此,教练员应及时了解这些变化并采取相应的调控方法,使运动员不断向既定训练目标靠近。所以,优秀羽毛球运动员在训练过程中所表现出来的状态特征,是教练员实施控制的重要基础,也是建立优秀羽毛球运动员竞技能力状态诊断物元模型的出发点。为便于表述,先界定几个概念如下:
1)状态特征:描述运动员在训练过程中正常状态下所表现出来的典型指标,记为v。
2)状态特征集:由状态特征组成的集合,描述的是运动员训练过程中所表现出来的整体状态,用V表示,则有 V=(v1,v2,…,vn),其中 v1,v2,…,vn表示n个状态特征。
3)目标状态:在运动员达到既定训练目标后表现出来的状态,它由目标状态特征集来表征,记为Xi。
4)过程状态:由起始状态出发向目标状态演进的中间状态,由过程状态特征集来描述,记为Xpi,则显然有:XiÌXpi。
由以上规定出发,构建优秀羽毛球运动员竞技能力状态物元模型如下:
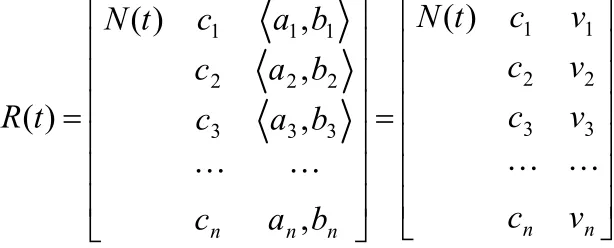
其中,N(t)表示受控运动员,(c1,c2,…,cn)为运动员的状态特征集,(v1,v2,…,vn)表示该运动员状态特征集的指标量度。由于运动员状态随时间t发生变化,可以用区间〈ai,bi〉来表示ci这一状态特征的取值范围。必须说明的是,由于运动员训练状态各项指标的含义不同,因此ci在〈ai,bi〉内的量度值既可以是数值化的,也可以是非数值化的,既可以是连续的,也可以是离散的。R(t)即表示运动员状态随时间变化的动态系统物元。为简化起见,在实际的运动训练物元模型构建过程中,可以选取特征值变化较大或权重值较大的状态特征来研究,对权重值较小或变化幅度不大的状态特征可以忽略不计。
1.2 优秀羽毛球运动员竞技状态诊断的物元模型

表示为目标状态物元,(c1,c2,…,cn)为运动员状态特征集,(X01,X02,…,X0n)是运动员在目标状态时各项训练特征的取值,其中X0i=〈a0i,b0i〉,i=1,2,…,n。令

表示该运动员整个训练过程的总变化物元模型,Xpi=〈ap1,bpi〉,i=1,2,…,n,其中 api为 ci这一特征的起始状态值,,bpi为 ci之一特征的目标状态值。显然有X0iÌ Xpi,i=1,2,…,n。
对过程状态物元在某一特定时间上的结果,即该运动员在该时间各项训练状态的测试值,可由以下物元表示:
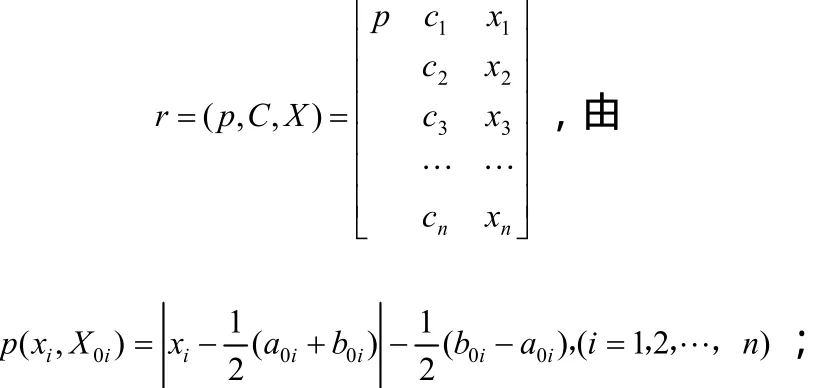
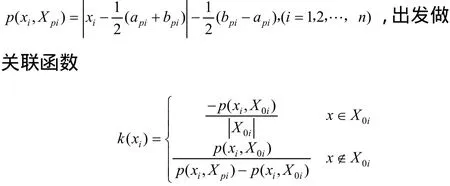
其中P(xi,Xpi)为点 xi与区间 Xpi的距离,即运动员现实状态与目标状态的距离。关联函数 k(xi)可以表示 xi与 Xpi的关联程度,k(x)>0则表示点 xi属于 Xpi,数值越大相关性越高;k(x)<0表示点xi不属于Xpi,数值越小相关性越高。
根据训练项目的特点,由专家组确定状态特征集(c1,c2,…,cn)的权重系数(λ1,λ2,…,λn)并计算度。当k(x)≥0时,表示运动员竞技状态较好,综合情况已基本达到或超过训练目标,达到或超过的程度视k(x)的值而定;当-1≤k(x)<0时,表示运动员的竞技能力状态处于潜伏期,有继续提高的可能,我们可以进一步分析各指标关联函数的大小来明确下一阶段训练的方向与重点,即通过找出k(xi)<0的指标进行针对性训练,强化和改进运动训练的薄弱环节,通过运动训练的延续进行和有效控制来促使运动员竞技能力状态不断向目标状态靠近;当k(x)<-1时,表示运动员训练情况不佳,竞技能力没有明显增加,应该适当调整训练计划或训练方法。无论k(x)的取值状况如何,均可以通过各状态特征的 k(xi)来分析其对运动员综合竞技能力状态的影响情况,以确定应该加强哪些指标的训练。
2 优秀羽毛球运动员竞技状态诊断的实例分析
下面以广东省羽毛球队运动员王某某 2011年训练目标模型为例,构建其竞技能力状态诊断的物元模型。为确保选取的特征指标能全面反映优秀羽毛球运动员的竞技状态,根据程勇民[6]的研究成果,选取了12个能全面反映优秀羽毛球运动员竞技能力状态的典型指标:“克托莱指数、身高、上肢无氧功率、下肢5 s峰值功率、30 s平均功率、立定跳远、专项跑动时、拍数/回合、主动失误次数/总拍数、翻转反应时、操作思维步数、意志力”,在考虑测试手段的可操作性与咨询领域专家的基础上[7],建立了由5个典型的状态特征指标组成的状态特征集(见表1)。
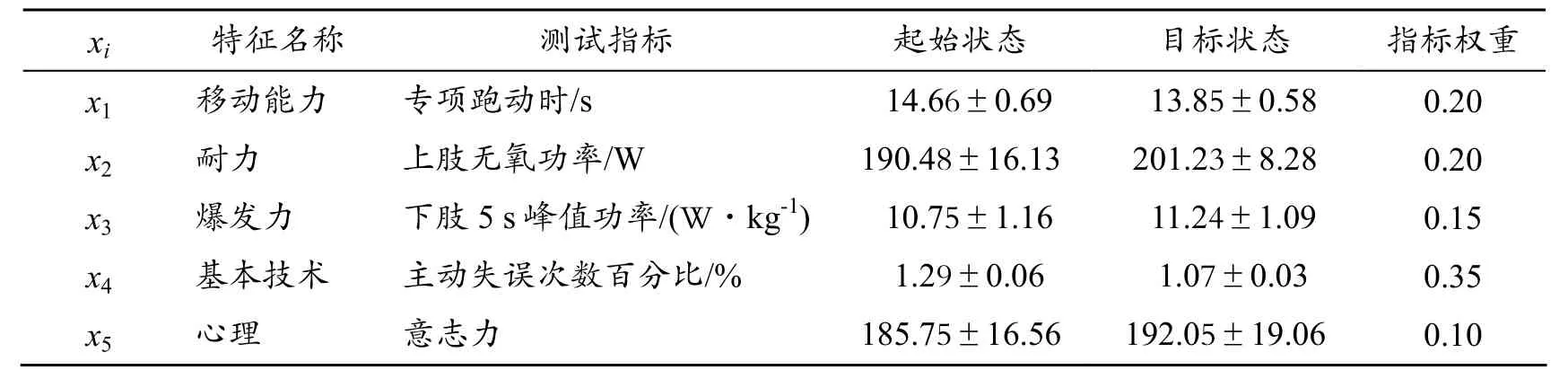
表1 王某某2011年训练目标模型
其中,起始状态数据为运动员训练之前的竞技能力现实状态,由实际测量获得(运动员心理特征状况水平采用“BTL-YZ-1意志量表”来测试);目标状态数据为运动员训练目标模型的参照值;指标权重由专家采用层次分析法给出。为便于综合处理,对以上数据为表2。
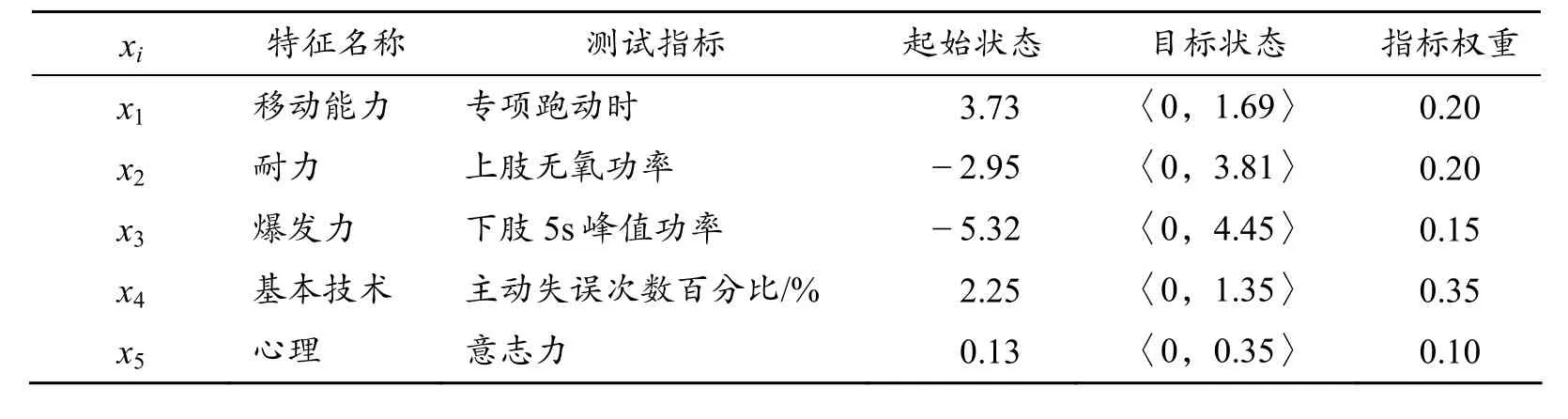
表2 王某某2011年训练目标模型无量纲处理结果
从表2出发,构造目标状态物元为:

总变化物元模型为:

根据该运动员在2011年12月测定的5项指标x1、x2、x3、x4、x5分别为:14.12 s、195.13 W、11.27 W/kg、1.14%、190.76。依据公式计算关联函数值分别为:

这一状态与目标状态的关联度:
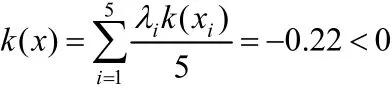
该结果说明该运动员此时的训练情况不算理想(k(x)<0),没有达到目标状态,但处于潜伏期,有继续提高的可能。进一步分析各指标的关联函数可以发现,k(x1)=-2.44和k(x2)=-0.36小于零,是使该运动员竞技能力没有产生明显变化的主要原因。因此,为了提高该运动员的竞技状态,需采用更有效的方法来增强其移动能力和耐力,特别是要加强其移动能力,这是促使其竞技状态产生变化的关键。
3 结论
1)优秀羽毛球运动员竞技状态诊断的物元模型,从运动员训练的基本状态出发,通过物元转换,能有效地确定运动员当前状态与目标状态的关联度,并能通过各分项指标的关联函数找到影响运动员竞技状态的关键因素,从而能够进行合理的诊断。
2)可拓评价方法采用关联函数进行定量计算,可以使评价简单易行,这较其他方法而言具有一定的优越性。同时,该方法能明确指出待评运动员提高竞技能力状况需要改善的指标,为提高运动员竞技能力状态提供参考。
3)在实际训练中还可以尝试选取运动员训练过程中的多个时间点来进行物元诊断,构成诊断结果序列,通过对该序列各数据的比较分析,可以有效地判断运动员竞技状态的走势,以便长期跟踪训练效果。
[1] 王清. 我国优秀运动员竞技能力状态诊断和监测系统的研究建立[M]. 北京:人民体育出版社,2004.
[2] 田麦久. 运动训练学[M]. 北京:人民体育出版社,2000.
[3] 蔡文. 物元模型及其运用[M]. 北京:科学技术文献出版社,1994.
[4] 卢绪祥,李录平. 凝汽器运行状态的物元模型及可拓评价方法[J]. 热能动力工程,2008,23(1):24-27.
[5] 李少丹. 论竞技状态的复杂性[J]. 北京体育大学学报,2009,32(6):11-14.
[6] 程勇民,梁承谋,阎济宁,等. 优秀羽毛球运动员科学选材研究[J]. 广州体育学院学报,2007,27(4):53-56.
[7] 邱宪祥. 中国优秀羽毛球运动员竞技能力结构特征及台湾羽毛球运动员选材标准[D]. 北京:北京体育大学,2006:86-98.

