部分重叠覆盖的数值流形方法初步研究

祁勇峰，苏海东，崔建华

(长江科学院a.水利部水工程安全与病害防治工程技术研究中心;b.材料与结构研究所，武汉 430010)

1 研究背景

数值流形方法［1］(以下简称流形法)是留美学者石根华博士提出的一种新型数值计算方法。该方法采用了覆盖的概念和2套相互独立的网格体系。覆盖，或称为数学覆盖，用以定义各个区域的局部函数。2套相互独立的网格体系，即反映数值解精度的数学网格和表示几何边界和材料分区的物理网格，将整个研究区域划分成有限个相互重叠的区域，这些区域被称为(物理)覆盖，在各个覆盖上独立定义局部覆盖函数，通过权函数加权平均得到整个求解域上的总体函数。2套网格的交集，称为流形元，和有限元一样，是基本计算单元，但可具有复杂任意的形状。为保证任意形状的流形元的积分精度，流形法多采用单纯形积分。

在结构应力分析方面，流形法相对于有限元法的优势主要体现在两方面:一是数学网格与物理网格相互独立，两者边界可以不重合，只要求前者覆盖后者，因此可采用规则的数学网格对复杂的物理区域进行切分形成流形元，切分过程仅涉及简单的几何运算，前处理方便;二是可以通过提高覆盖函数阶数或构造特殊覆盖函数来提高数值解的精度。

当前的流形法研究多采用有限单元网格来构造数学网格。对任一结点，与该结点相连的所有有限元形成一个数学覆盖，这样，任一原始的有限元网格就是其结点覆盖的重叠部分，或者说，定义于有限元结点上的覆盖在有限单元的区域内完全重叠，本文称之为完全重叠覆盖的流形法。这种方法能够充分利用有限元法的基本公式，在流形法的初步应用研究中发挥了重要的作用［2－5］。但研究表明，在人们实际比较关注的一些结构关键部位，如孔周边、裂纹尖端附近等，2套网格的不匹配可能造成计算精度的下降，流形法的计算结果往往达不到常规有限元法的精度水平。解决上述问题的一种途径是对数学网格进行人工干预，如文献［6］将数学网格结点布置在上述关键部位，虽能起到一定效果，但加大了人工工作量及处理难度，抵消了流形法在前处理上的一些优势。

针对上述问题，石根华博士指出，现在的流形法只是一个初级版本。实际上，流形覆盖有着丰富的内涵，是非常灵活的。数值流形方法的基本思想来自于数学上的流形，即部分重叠的非空开集之并。在数学上，对于各种复杂的几何形状，用统一的坐标去描述并不方便。因此，近代数学的一个重要分支——微分几何提出了流形思想，用各种独立的覆盖反映各自区域的几何特征。覆盖与覆盖之间的重叠区域只是为了保持覆盖之间的联系，或曰协调性(为保证积分的唯一性，需要引入各覆盖的权函数，并使权函数之和为1，这就是单位分解思想)。因此，原始的流形思想本身就是以独立的覆盖(即非空开集)为主，以其重叠区域为辅。

为此，石根华博士提出一种新的研究思路——部分重叠覆盖的流形法。该方法采用以独立覆盖为主的分析方式，独立覆盖之间仅用较小的重叠区域保持连续性。初步分析，部分重叠覆盖的流形法至少存在以下优点:便于在局部区域采用特殊的覆盖函数以适应物理场的局部特征，比如在裂纹尖端附近采用特殊的解析解级数，收敛性要比通常的多项式逼近快得多，这样就可以将不同区域的多种求解形式协调地联系起来进行联合求解，从而实现局部解析法与其周边数值解的完美结合;对独立的覆盖函数进行收敛性分析，不涉及其它覆盖，比完全重叠下的覆盖精度分析要方便;相邻覆盖之间的联系仅限于其较小的重叠部分，在保持协调性的同时又降低了自由度之间的相互影响，能有效地改善方程组的性态，有利于方程组的快速迭代求解。

作为部分重叠覆盖流形法的首次尝试，本文基于矩形覆盖，给出部分重叠的覆盖形式、部分重叠覆盖流形法的基本公式及其实现方式，对该方法在结构分析中的有效性进行初步验证，为下一步的研究打下良好的基础。

2 完全重叠的覆盖形式

结合一个简单的例子来说明覆盖、网格、重叠覆盖的概念。如图1(a)所示的椭圆形的物理区域(物理网格)以及矩形有限元数学网格(编号为a—p)，经过切割操作后形成物理覆盖系统(着色区域)。以网格e为例，在其4个结点中，与结点1相连的所有有限元数学网格(a，e)构成结点1的数学覆盖，与结点2相连的有限元网格(a，b，e，f)构成结点2的数学覆盖，结点3和结点4的数学覆盖类似，分别见图1(b)—图1(e)，图中所示的矩形网格中的着色区域即为物理覆盖。这4个物理覆盖的交集为图1(f)的数学网格e的着色区域，定义为流形元，图中可见流形元可以仅占据网格内的部分区域，并具有任意的形状。

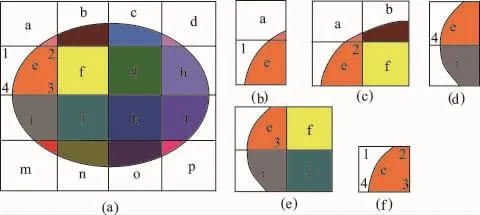
图1 完全重叠的数学覆盖Fig.1 Completely overlapping math cover

从这个例子中可见，每个有限单元网格正好就是其几个结点上的数学覆盖的共同区域，或者说，这几个覆盖在有限单元的区域内完全重叠，这就是通常所见的完全重叠的覆盖形式。

3 部分重叠的覆盖形式

仍考虑图1中的椭圆形物理区域，图2为矩形网格的部分重叠覆盖系统示意图。其中，图2(a)中a—p所示的矩形网格为数学覆盖，覆盖之间为较小的重叠区域，图2(b)的着色区域即为物理网格与数学网格(覆盖)相互切割后形成的物理覆盖。

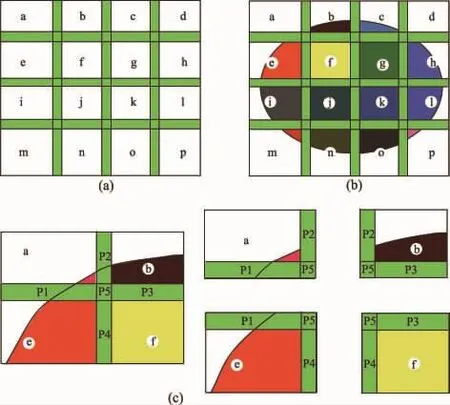
图2 部分重叠的数学覆盖Fig.2 Partially overlapping math cover

以图2(c)中的局部 4 个数学覆盖 a，b，e，f为例，每个覆盖包含一个独立覆盖区域(图2(c)中较大的矩形)和3个覆盖重叠区域，其中，P1—P4为相邻两个覆盖之间的重叠区域，P5为4个覆盖共同的重叠区域。在完全重叠覆盖的流形法中，流形单元定义为覆盖重叠的公共部分，而对于部分重叠覆盖的流形法，流形元还应包括独立覆盖中的物理区域(物理覆盖)。

4 部分重叠覆盖的实现技术

与通常所见的完全重叠的覆盖体系不同，部分重叠的覆盖体系涉及到众多的独立覆盖及其周边较小的覆盖重叠区域，本来需要编制新的程序来实现。但实际上，在完全重叠的矩形覆盖体系下，仅需采用简单的结点之间强制约束的技术，就可以很方便地实现部分重叠的覆盖形式。以下结合图2(c)中所示的局部区域说明实现过程，见图3(a)。

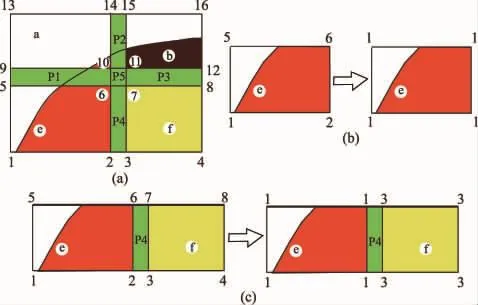
图3 采用自由度约束实现部分重叠覆盖Fig.3 Partial overlapping cover obtained by using freedom constraint

首先考察图3(b)的数学网格1－2－6－5，网格内的流形元位移函数为

式中:Ui为定义在结点i上的多项式覆盖函数;Wi为权函数，

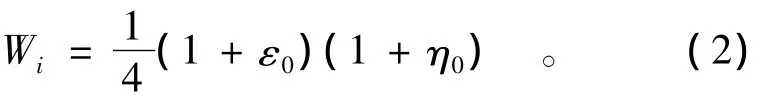
式中:ε0=εiε，η0=ηiη，(ε，η)为网格内任意点的局部坐标;(εi，ηi)为结点的局部坐标，见图4。权函数满足

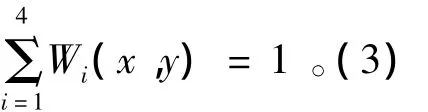
将结点2，5，6“强制约束”到结点1，即令U2=U3=U4=U1，考虑到式(3)，则式(1)成为

图4 矩形数学网格Fig.4 Rectangular math mesh

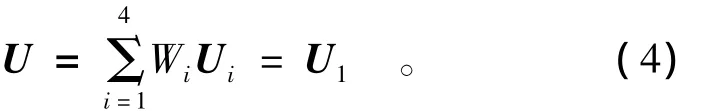
即在数学网格中保持权函数为1，使原始的完全重叠覆盖1－2－6－5成为独立覆盖1。其他的独立覆盖类似，如图3(a)所示，结点4，7，8约束到结点3，结点10，13，14 约束到结点9，结点12，15，16约束到结点11，分别形成独立覆盖3，9，11。

再考察上述4个覆盖之间的重叠区域，以图3(c)所示的覆盖e和f之间的交叉区域P4(结点2－3－7－6)为例。结点2和6为同一覆盖，局部覆盖函数为U1，结点3和7也为同一覆盖，局部覆盖函数为U2，则网格内的位移函数为

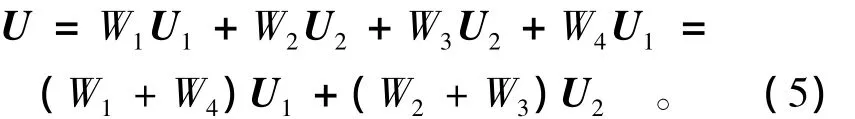
式中W1+W4=(1－ξ)/2，W2+W3=(1+ξ)/2，为一维的权函数(ξ为局部坐标，－1≤ξ≤+1)，因此P4区域正好是2个一维覆盖的重叠区域，在独立覆盖1的边界1—1上满足ξ=－1，独立覆盖3的边界3—3上满足ξ=1。P1—P3的重叠区域的情况类似。

对于4个覆盖的重叠区域P5，位移函数与完全重叠覆盖的情况一致。

在完全重叠覆盖流形法程序的基础上，仅需加入结点自由度之间的关联程序段，就可以实现部分重叠的覆盖，实现过程简单方便。在覆盖之间的重叠区域，比如图3(1)所示的P1—P5，数学网格的各结点对应于不同的独立覆盖，需要推导相应的流形元计算公式。

5 部分重叠覆盖的流形单元分析

在完全重叠覆盖的流形法中，基于多项式覆盖函数和矩形数学网格，采用矩阵特殊运算推导了流形元计算公式，但各结点采用的是相同的覆盖函数［7］。部分重叠覆盖流形法的计算公式与前者大体相同，但可灵活实现不同结点采用不同的覆盖函数，以下相应的位移函数与刚度矩阵公式。

5.1 位移函数

矩形网格中的位移函数可表示为

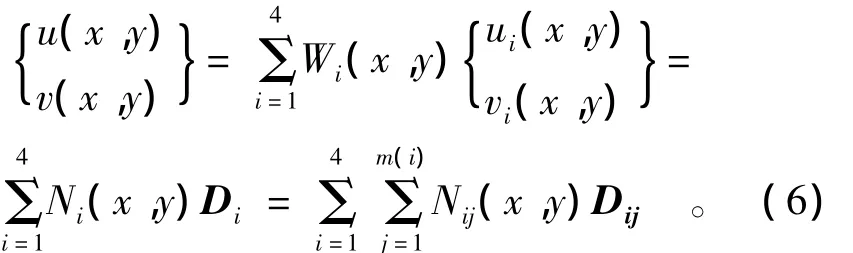
式中:权函数

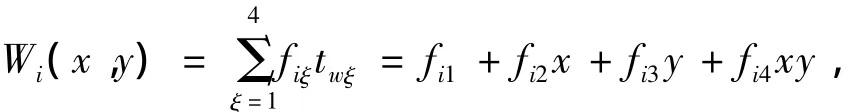
其中:

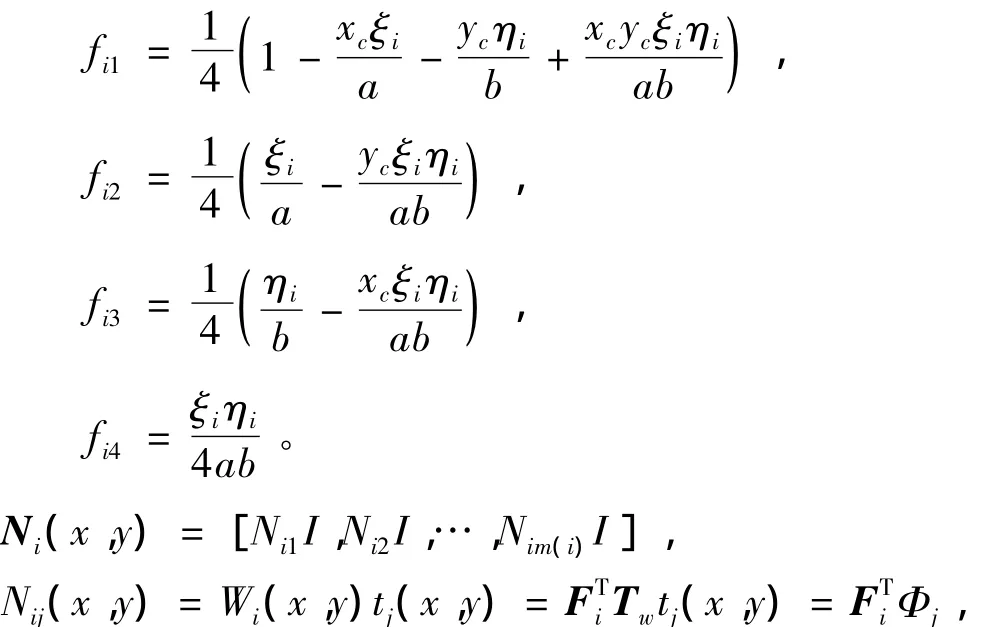
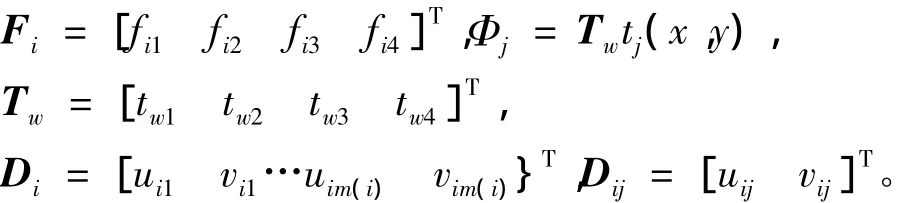
式中:定义在结点i上的多项式覆盖函数项数为m(i);uij，vij为覆盖函数的系数;Fi是权函数的系数列阵;ξi，ηi(i=1～4)为4 个结点的局部坐标，依次为(－1，－1)，(1，－1)，(1，1)，(－1，1);xc，yc为矩形网格的形心坐标;a，b为矩形网格的边长;twξ是多项式基底，I为2阶单位矩阵。

5.2 刚度矩阵

流形元应变矩阵为

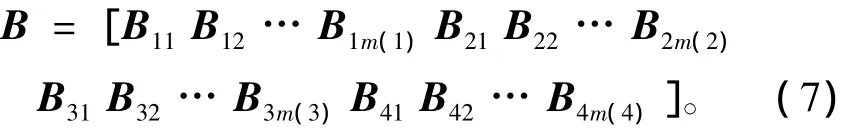
式中，

刚度矩阵为

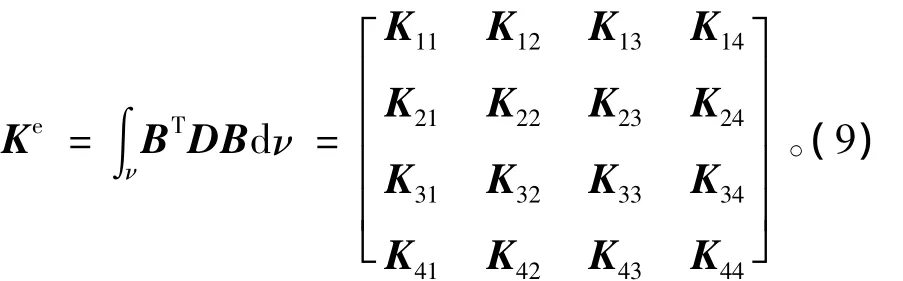
其中，

流形元刚度矩阵的子块(2×2)也可表示为

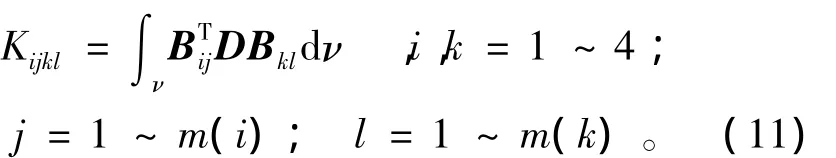
式中:D为弹性矩阵;B为几何矩阵;m(i)，m(k)分别表示结点覆盖i，k的多项式项数。

6 算例分析

如图5所示的重力坝，坝高100m，坝底长为60m，坝顶宽度20m，库水深80m。坝体弹性模量为30 GPa，泊松比为0.167。计算上游面承受库水压力情况下的应力和变形。采用稠密网格的有限元计算结果作为对比，划分1 080个4结点等参元，结点总数为1 183个。

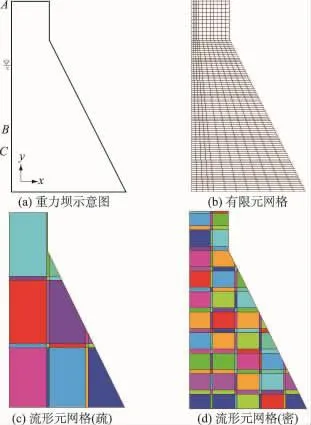
图5 计算网格Fig.5 Computational mesh

采用疏密程度不同的流形元网格进行计算，其中:疏网格有8个独立覆盖，包括其重叠区域在内共有流形单元21个;密网格有36个独立覆盖，流形单元总数为112个。计算模型的底部全约束。计算结果及与有限元的对比见表1和图6、图7，对比分析上游表面的x向位移及x，y向的应力，其中水位以下的x向应力应等于该点处的静水压力。

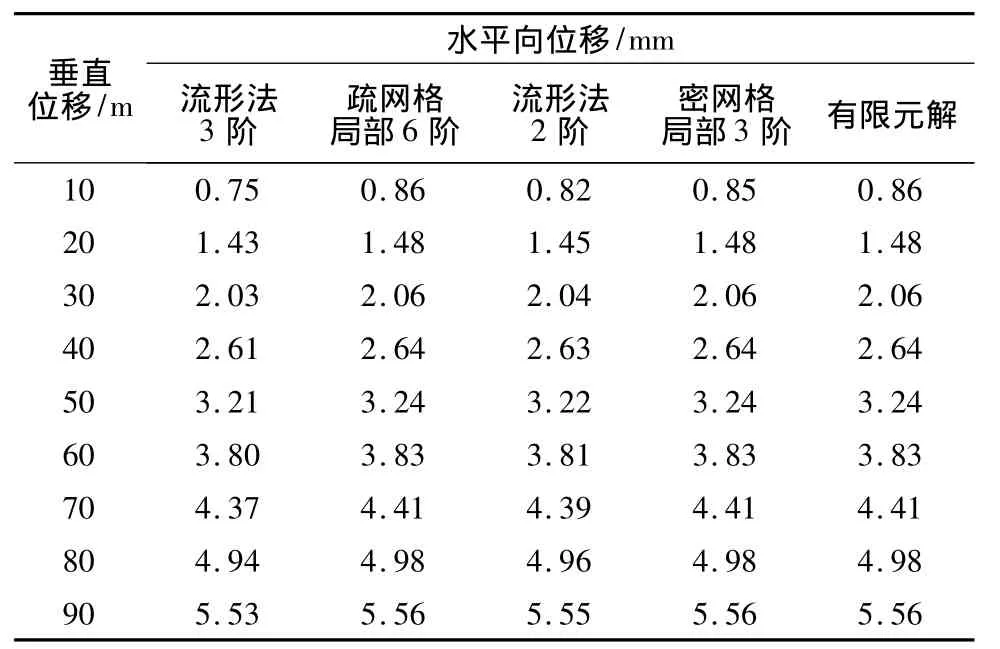
表1 上游面特征点x向位移对比Table 1 Comparison of horizontal displacements on the upstream surface calculated by manifold method and finite element method

表1的上游面x向位移显示，疏网格的3阶流形法计算结果与有限元总体上接近，但在靠近坝踵的部位(y=10m)由于约束的影响计算结果稍差。仅对上游底部的独立覆盖升阶，保持其他覆盖的阶数不变，至6，7阶时，位移与有限元解一致。密网格3阶流形法的结果与有限元解一致。

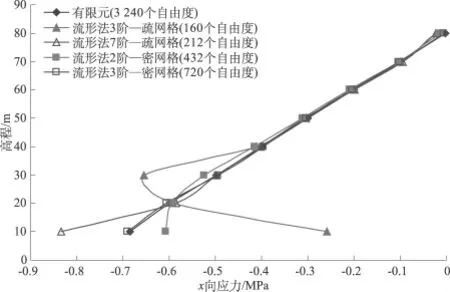
图6 上游面特征点x向应力对比Fig.6 Comparison of horizontal stresses on the upstream surface calculated by manifold method and finite element method

图7 上游面特征点y向应力对比Fig.7 Comparison of vertical stresses on the upstream surface calculated by manifold method and finite element method

图6和图7的上游面x向及y向应力对比表明，疏网格采用3阶流形法时，在中上部(y=40m以上)与有限元的结果接近，而在底部覆盖处由于约束的影响难以获得较好的结果。因此，将上游底部的独立覆盖升至7阶后，其他覆盖的阶数保持不变，x向、y向应力比3阶情况有较大改善，除了在靠近坝踵的部位(y=10m)处计算结果稍差外，其它部位与有限元解基本一致。密网格的2阶流形法结果稍差，将上游的10个独立覆盖升至3阶，其他覆盖保持2阶不变，计算结果与有限元解很接近。

以上算例表明，部分重叠覆盖的流形法可以得到较好的计算结果。对于某些计算结果不理想的独立覆盖区域，通过提高该覆盖中的多项式阶数也可以提高计算精度，且对周边覆盖中的计算结果影响较小。但对于应力和变形过于复杂的独立覆盖区域往往需要很高的覆盖函数阶次，因此有时单纯提高阶次的效果不佳，而相比之下通过加密覆盖，即使采用低阶覆盖函数也可以得到很好的计算结果。

7 结语

本文将现有的基于完全重叠覆盖的流形法扩展到一般意义上的流形研究——部分重叠覆盖的流形法，通过单个矩形数学网格各结点之间的强制约束方式，很方便地将完全重叠的覆盖形式及流形法公式转化为部分重叠的覆盖形式及公式，算例分析初步验证了这种新型流形法的有效性。

部分重叠覆盖的流形法是一种以独立覆盖分析为主的全新计算模式，本文的工作仅仅是其研究的开始。我们在进一步的研究中开展了以下工作:在独立覆盖中采用特殊的覆盖函数以适应物理场的局部特征，如应用裂纹尖端解析覆盖计算裂纹尖端的位移场及应力强度因子［8］;根据需要进行大、小覆盖之间的疏密布置并保持协调过渡，使其具有更大的灵活性;采用部分离散的思想初步形成基于流形思想的有限条分析方法，将以往只能用于规则形状的有限条法扩展到分析复杂形状。这些工作将另文介绍。

致谢:部分重叠覆盖的流形法思想是由石根华博士提出的，本文的研究工作得到了石根华博士的悉心指导，在此表示由衷的感谢!

［1］石根华.数值流形方法与非连续变形分析［M］.北京:清华大学出版社，1997.(SHI Gen-hua.Numerical Manifold Method and Discontinuous Deformation Analysis［M］.Beijing:Tsinghua University Press，1997.(in Chinese))

［2］彭自强，葛修润.数值流形方法在八结点有限元网格上的实现［J］.武汉大学学报(工学版)，2004，37(2):72－76.(PENG Zi-qiang，GE Xiu-run.Numerical Manifold Method on Eight-node Isoparametric Element Meshes［J］.Engineering Journal of Wuhan University，2004，37(2):72－76.(in Chinese))

［3］林绍忠，明峥嵘，祁勇峰.用数值流形法分析温度场及温度应力［J］.长江科学院院报，2007，24(5):72－75.(LIN Shao-zhong，MING Zheng-rong，QI Yong-feng.Thermal Field and Thermal Stress Analysis Based on Numerical Manifold Method［J］.Journal of Yangtze River Scientific Research Institute，2007，24(5):72－75.(in Chinese))

［4］苏海东，黄玉盈.数值流形方法在流固耦合谐振分析中的应用［J］.计算力学学报，2007，24(6):823－828.(SUHai-dong，HUANGYu-ying.Application of Numerical Manifold Method in Fluid-solid Interaction Harmonic Analysis［J］. Journal of Computational Mechanics，2007，24(6):823－828.(in Chinese))

［5］JIANG Qing-hui，ZHOU Chuang-bing，LI Dian-qing.A Three-Dimensional Numerical Manifold Method Based on Tetrahedral Meshes［J］.Computers ＆ Structures，2009，87(7):880－889.

［6］苏海东，谢小玲，陈 琴.高阶数值流形方法在结构静力分析中的应用研究［J］.长江科学院院报，2005，22(5):74－77.(SU Hai-dong，XIE Xiao-ling，CHEN Qin.Application of High-order Numerical Manifold Method in Static Analysis［J］.Journal of Yangtze River Scientific Research Institute，2005，22(5):74－77.(in Chinese))

［7］林绍忠，祁勇峰，苏海东.基于矩阵特殊运算的高阶流形元单元分析［J］.长江科学院院报，2006，23(6):36－39.(LIN Shao-zhong，QI Yong-feng，SU Hai-dong.Element Analysis of High-Order Numerical Manifold Method Based on Special Matrix Operations［J］.Journal of Yangtze River Scientific Research Institute，2006，23(6):36－39.(in Chinese))

［8］SU Hai-dong，QI Yong-feng.A Novel Numerical Method for Computing Stress Intensity Factors［J］.Applied Mechanics and Materials，2012，204－208:4486－4489.