中、长波热红外系统辐射测温精度比较

孙志远，赵 楠

(中国科学院长春光学精密机械与物理研究所，吉林长春130033)

1 引言

热红外系统最优的波段是哪个波段?有很多针对中波(3～5μm)和长波(8～12μm)系统的研究［1－3］，测量用的热红外系统最优波段问题也在相关文献［4］～［6］中有过讨论，然而，分析结果并没有明确地阐述中波红外系统和长波红外系统之间的不同，也没有确定测量用热红外系统的最优波段。

本文尝试解决测量用热红外系统的最优波段问题。基于理论公式，针对信号干扰(发射率估计误差、大气透过率、目标反射辐射和光学系统辐射变化等)对信号测量精度和温度测量精度的影响进行分析。综合考虑导弹、飞行器和坦克等军事目标的温度特性，我们定义的典型温度范围为270～900 K(－3～627℃)，而且以0．5和0．9这两个发射率值为例进行分析。

2 基本理论

首先先做几点假设:第一，光学系统被认作是一个单独的组分，透过率假设为τ0(λ);第二，忽略目标与系统之间的大气辐射和目标反射的背景辐射的影响;第三，中波系统和长波系统的光学系统、结构、电子学、温度和光谱分辨率等状态是近似相同的。

满足以上假设后，红外探测器接收到的能量只有参考源的辐射能和光学系统辐射，测量的信号可以表示如式(1)所示［7－8］:

式中，k是信号变换系数;εL是目标的发射率;λ1～λ2是探测器光谱响应波段范围;M(λ，T)是温度T和波长λ处的光谱辐射能;Tob是目标的温度;Topt是光学系统的温度;τ0(λ)为光学系统的透过率;s(λ)是红外探测器相对光谱响应曲线。

利用普朗克公式，可以获得公式(1)的新形式:

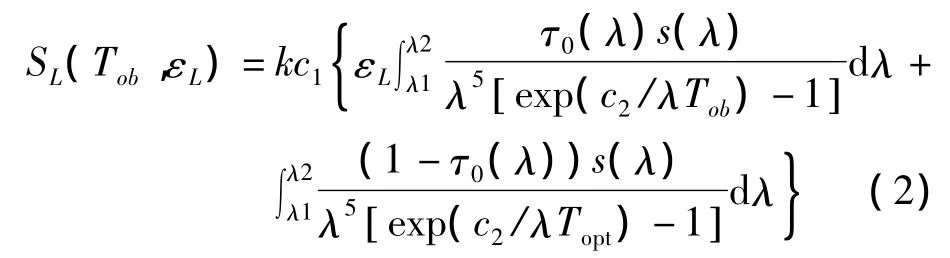
式中，c1为第一辐射常数，c2为第二辐射常数常量。

3 DRF函数

信号测量过程中的干扰会影响温度测量误差，然而，我们感兴趣的是这种影响会对测量产生多大误差。首先，需要找到信号测量误差和温度测量误差之间关系。

对公式(2)求微分，得到:

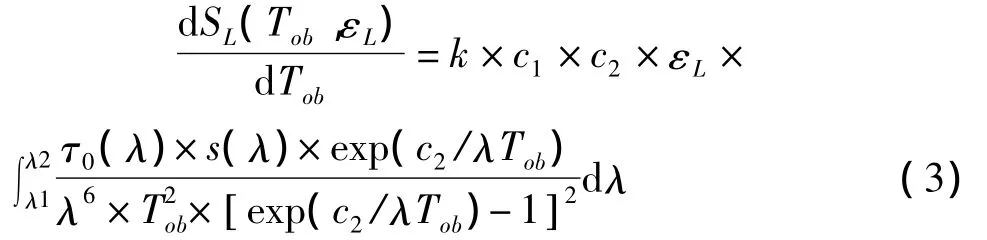
公式(3)乘dTob/SL，得到:

其中:

当信号SL有微小变化时，信号测量误差和温度测量误差之间的关系公式如下所示:

公式(6)表达了干扰引起的信号测量误差与温度测量误差之间的关系函数。

DRF(Tob，εL，Topt)可以被称作抗干扰函数，因为它代表了系统的抗信号干扰能力。如图1所示为中、长波红外系统的DRF图。

图1 3个发射率情况下中、长波红外系统的DRF曲线(光学系统温度293 K)Fig．1 DRF's ofmiddlewave and longwave TIS's for three values of object emissivity．The temperature of the optics is assumed to 293 K

从图1可以看出，在典型的温度范围内，中波红外系统的DRF数值比长波红外系统的DRF高，这就表明:相同大小的信号干扰对中波红外系统的温度测量精度影响要小一些。对于中波红外系统，DRF曲线从最高点向温度降低方向的快速下降是由光学系统辐射的影响引起的。

4 测量信号的干扰

上一节的结论表明:中波红外系统的抗干扰能力比长波红外系统要高。然而，温度测量精度不仅取决于红外系统的抗干扰能力，还取决于干扰的大小。DRF可以作为红外系统比较的一个质量因数，但比较这些系统最重要的质量因数是温度测量精度。

上一节介绍的SL是在理想情况下的信号输出，但是在实际工作中，红外探测器接收到的辐射主要包括以下5个部分［9－10］:首先是目标自身辐射:由目标的温度Tob和发射率εR决定;第二是目标反射的辐射:包括反射太阳、天空、周围物体和大气等反射辐射;第三是光学系统辐射:由光学系统温度Topt和光谱透过率τ0(λ)决定;第四是大气辐射:由大气温度、大气的光谱透过率τa和目标与红外系统的距离R决定;第五是太阳和其他辐射源散射到大气中的辐射:由目标与红外系统的距离R以及大气和环境的许多参数决定。

其中只有第一个成分包含了被测目标的有用信息，其他成分都是干扰源。不同环境情况下，大气辐射和太阳及其他辐射源的散射情况有很大不同，本文只考虑实验室环境中较近距离的情况，所以第四和第五两项辐射可以忽略不计。

实际工作状态下，探测器接收到的信号表示如下:

式中，εR是被测目标的真实发射率;τa是大气透过率;Tback是背景温度是光学系统的温度。

信号测量的相对误差可以表示为实际工作状态下测量的信号SR和理想情况下的信号SL的差值与理想情况下的信号SL的比值:

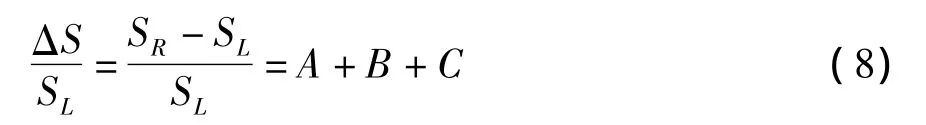
式中:

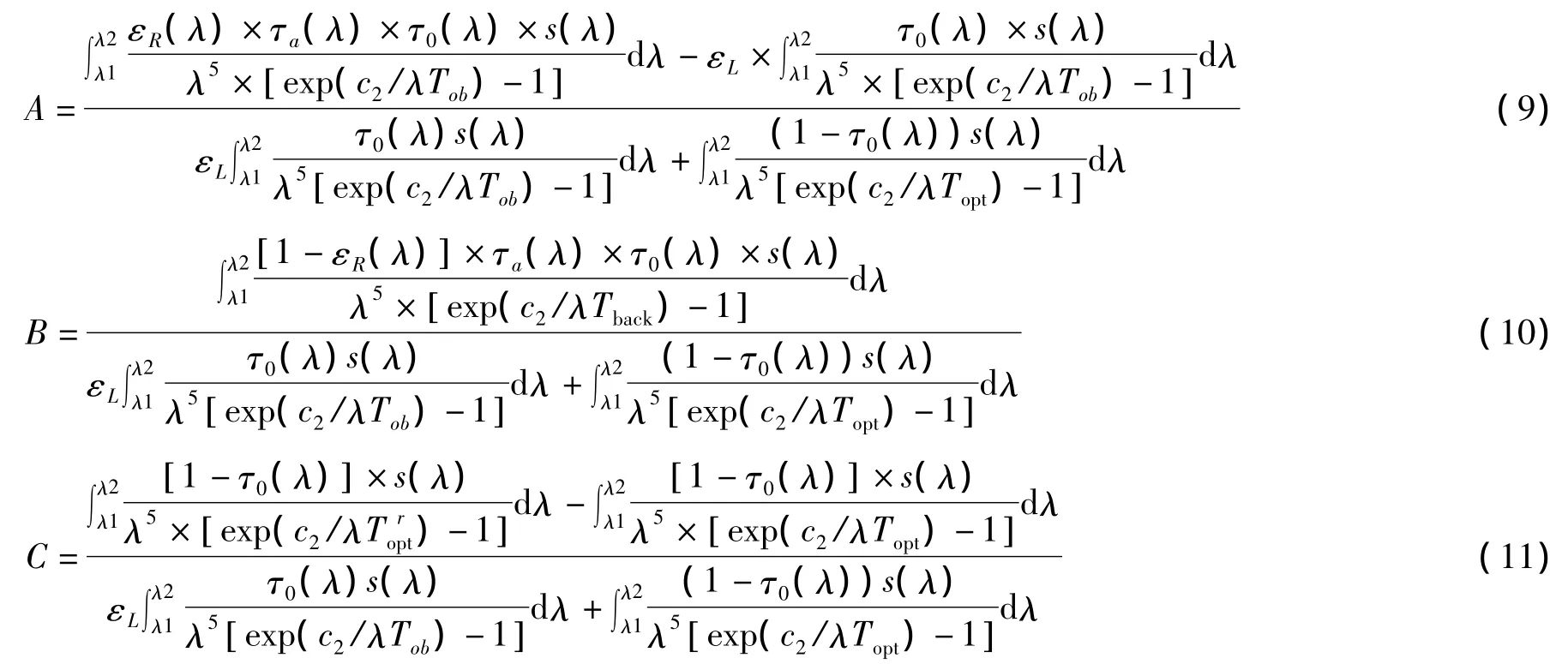
5 干扰引起的温度测量误差

成分A，B，C给出了干扰引起的信号测量误差信息，其中A是由目标发射率估计误差(当τa(λ)=1时)和大气透过率(当εR(λ)=εL时)误差共同影响，B是目标反射辐射的影响，C是光学系统辐射变化的影响，信号测量的总误差是所有以上误差项的总和，根据公式(6)可以计算温度测量误差。

5．1 发射率估计误差

影响热成像系统测温精度的一个最重要的因素是被测目标的发射率。发射率是一项难以被精确确定的参数，它取决于很多因素，比如表面温度、形状、观测角、波段等。基于实验结果，发射率估计误差约为5%。下面在发射率估计误差在5%以内的前提下分析信号测量误差和温度测量误差，如图2和图3所示。

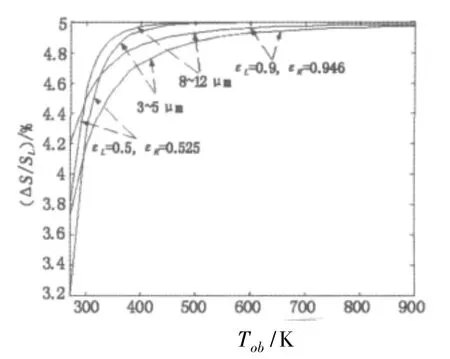
图2 目标发射率的估计误差引起的信号测量误差(光学系统温度293 K)Fig．2 error of the signalmeasurement caused by improperly assumed emissivity．The temperature of the optics is assumed to equal293 K

从图2可以看出，在低温段，信号测量误差与发射率大小有较大的关系，在高温段，变得比较平缓。温度测量误差取决于发射率的估计误差，而与发射率的大小无关，如图3所示。对于发射率估计误差引起的温度测量误差，中波红外系统小于长波系统，在典型温度范围内该项误差小于2．5%。

图3 目标发射率的估计误差引起的温度测量误差(光学系统温度293 K)Fig．3 error of temperaturemeasurement caused by improperly assumed emissivity．The temperature of the optics is assumed to equal 293 K

5．2 大气透过率

红外辐射在大气中会经过吸收和散射。大气传输取决于很多参数，为了分析大气的影响，通用计算方法是LOWTRAN或MODTRAN。假设目标的温度为500 K、发射率为0．5，大气透过率引起的信号测量误差和温度测量误差如图4和图5所示。

图4 大气透过率引起的信号测量误差(目标温度500 K，发射率0．5)Fig．4 error of the signalmeasurement caused by the limited transmittance of the atmosphere．the temperature of the object is equal to 500 K，and an emissivity equal to 0．5 has been assumed

图5 大气透过率引起的温度测量误差(目标温度500 K，发射率0．5)Fig．5 error of temperaturemeasurement caused by the limited transmittance of the atmosphere．the temperature of the object is equal to 500 K，and an emissivity equal to 0．5 has been assumed

从图4和图5可以看出，大气透过率引起的信号测量误差，中波系统比长波系统大;然而，对于温度测量误差，中波红外系统的误差稍大，在100 m的距离内小于2%。

5．3 目标反射辐射

不透明目标的反射率ρ等于1－ε。因此，高发射率目标测量时不会引起较大误差，但对于低发射率目标，反射的辐射引起的误差是很大的。反射辐射不仅和目标发射率相关，还与背景的温度相关。反射的辐射能是系统和系统后的一部分背景通过与系统光轴垂直的目标表面进入系统的，然而，实际应用中，很少有目标表面是完全平面的，操作者需要面对的更多是漫反射体，所以精确地计算目标反射的辐射是困难的。为了简化分析，使用背景温度进行分析，在适当的背景温度下计算的背景反射辐射影响如图6和图7所示。

图6 反射辐射引起的信号测量误差(背景温度为303 K)Fig．6 error of the signalmeasurement caused by the reflected radiation．the temperature of background is assumed to equal 303 K

图7 反射辐射引起的温度测量相对误差(背景温度为303 K)Fig．7 error of temperaturemeasurement caused by the reflected radiation．the temperature of background is assumed to equal 303 K

从图7可以看出，反射辐射引起的测温误差是较大的，尤其当目标发射率和温度都较低时。在中波和长波情况下误差都较大，但中波红外系统的误差较小一些。当目标的温度大于380 K时且目标的发射率大于0．5时，目标反射辐射引起的中、长波红外系统测温误差都在10%以内。

5．4 光学系统辐射变化

光学系统辐射在辐射定标和辐射测量中都存在，光学系统辐射的变化会引起温度测量误差。光学系统辐射是由光学系统光谱透过率和光学系统的温度决定的，第一个参数与环境参数有关，但可以被认为是一个常数。第二个参数与环境温度、空气流通度和系统结构有关。光学系统辐射变化引起的信号测量误差和温度测量误差如图8和图9所示。

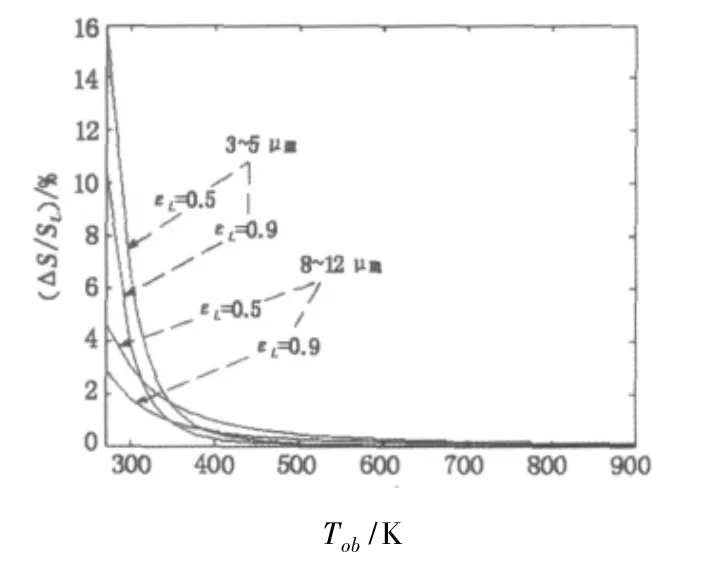
图8 光学系统辐射引起的信号测量误差(光学系统温度从293 K增加至303 K)Fig．8 error of the signalmeasurement caused by the radiation emitted by system optics．the temperature of the optics increased to 303 K from 293 K

图9 光学系统辐射引起的温度测量误差(光学系统温度从293 K增加至303 K)Fig．9 errors of temperaturemeasurement caused the radiation emitted by system optics．the temperature of the optics increased to 303 K from 293 K

如图9所示，目标的温度较低(小于300 K)时，中波红外系统比长波系统的测温误差大;但目标的温度较高(大于300 K)时，中波红外系统的测温误差比长波系统测温误差小。而且目标的发射率越低，该项误差越大。在典型温度范围内，光学系统辐射变化引起的中、长波红外系统测温误差均小于2．5%。

5．5 误差统计

当目标的发射率为0．5和0．9时，影响中、长波红外系统测温精度的各误差大小及总的测温误差如表1和表2所示。从表中可以看出，在典型的温度范围内，中波系统的测温误差都要小于长波系统的测温误差。而且在低温段，低发射率目标的测温精度远小于高发射率目标的测温精度。

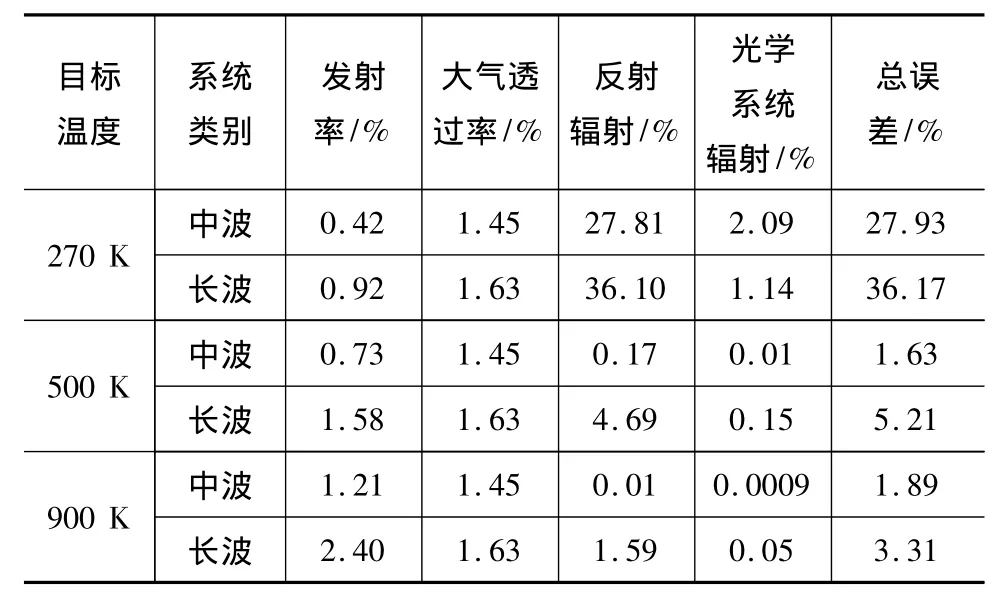
表1 中、长波系统测温误差(目标的发射率为0．5)Tab．1 errors of temperaturemeasurement of middlewave and longwave infrared systemswhen the target's emissivity is equal to 0．5

表2 中、长波系统测温误差(目标的发射率为0．9)Tab．2 errors of temperaturemeasurement of middlewave and longwave infrared systemswhen the target's emissivity is equal to 0．9

6 结论

温度测量精度是测量用热红外系统最重要的一个技术指标，结果表明:前述的几个干扰源对中波红外系统的影响较小。因此，我们可以得到这样的结论，中波红外系统比长波红外系统更适合进行辐射测温。但是必须要注意的是，以上结论有两个前提，一是实验条件为室内实验，二是目标的温度在270～900 K(－3～627℃)范围内。

前述分析计算了热红外系统在典型温度范围下的温度测量误差。当低发射率目标在较低温度时，温度测量误差尤其大，当目标的温度升高时，误差逐渐降低(唯一例外是发射率引起的误差)，所以热红外系统的温度测量误差不是可以忽略不计的。本文的理论对温度测量误差的计算和修正提供了有益的分析。但是对于复杂环境下的干扰源对测温精度的影响还需进一步的理论及实验研究。

［1］ G A Findlay，D A Cutten．Comparison of the performance of 3 ～ 5 μm and 8 ～ 12μm infrared systems［J］．Appl．Opt，1989，28:5029 －5037．

［2］ T Jaeger，A Nordbryhn，P A Stokseth．Detection of low contrast targets at 5 μm and 10 μm:a comparison［J］．Appl．Opt，1972，11:1833 －1835．

［3］ R Longshore，PRaimondi，M Lumpkin．Selection of detector peak wavelength for optimum infrared systems performance［J］．Infrared Phys，1976，16:639 －647．

［4］ JA Abel．Radiometrics accuracy of forward looking infrared systems［J］．Opt．Eng，1977，16:241 －248．

［5］ SP Braim．Technique for the analysis of data from an imaging infrared radiometer［J］．Infrared Phys，1988，28:255－261．

［6］ D S Fraedrich．Method in calibration an error analysis for infrared imaging radiometer［J］．Opt．Eng，1988，30:1764－1768．

［7］ Sun Zhiyuan，Zhu Wei，Qiao Yanfeng，et al．Atmosphere amending research in infrared radiation characteristic measurement［J］．Laser ＆ Infrared，2010，40(2):162 －165．(in Chinese)

孙志远，朱玮，乔彦峰，等．红外辐射特性测量中环境影响的修正研究［J］．激光与红外，2010，40(2):162－165．

［8］ Ju Yangfeng，Xue Jianguo，Liang Dongming，et al．Infrared radiation characteristic and detection of the terminal-sensitive projectile［J］．Laser ＆ Infrared，2012，42(2):157 －160．(in Chinese)

巨养锋，薛建国，梁冬明，等．末敏弹红外辐射特性及探测［J］．激光与红外，2012，42(2):157 －160．

［9］ Sun Chengming，Yuan Yan，Huang Fengzhen，et al．Modeling and simulation on infrared imaging characteristics of space target［J］．Infrared and Laser Engineering，2012，41(3):563 －568．(in Chinese)

孙成明，袁艳，黄锋振，等．空间目标红外成像特性建模与仿真［J］．红外与激光工程，2012，41(3):563－568．

［10］ Liu Juan，Gong Guanghong，Han Liang，et al．Modeling and simulation of airplane infrared characteristic［J］．Infrared and Laser Engineering，2011，40(7):1209 －1213．(in Chinese)

刘娟，龚光红，韩亮，等．飞机红外辐射特性建模与仿真［J］．红外与激光工程，2011，40(7):1209 －1213．