海域面积计算精度影响因子甄别与评价

赵晓龙，胡光海，王长青

(1. 国家海洋局 第一海洋研究所，山东 青岛 266061； 2. 中国石油天然气管道局 天津设计院，天津 300457)

海域面积的量算是海域使用论证的基础工作，是国家、各省市实时了解海域使用动态变化的基础技术指标，更是“控制单个项目用海面积，控制不同行业单个用海项目面积标准，防止盲目圈海占海和浪费海域资源”[1]的基本依据，具有重要的政治和经济意义。

传统海籍调查中海域面积的量算多采用解析法测量方法[2]，但地球是一个不规则椭球体，采用传统基于平面的欧式测量方法进行小比例尺海洋测量时，会由于地图投影等原因导致测量面积变形，严重影响海域面积的量算精度。根据海域管理工作的需要，探讨了海域面积计算精度影响因子并进行了定量化评价。

1 海域面积量算现状

目前，在平面及曲面上量算海域面积的方法很多，但可查阅的能科学、真实地反映海域实际面积的量算方法并不多。国家亦未公布一部内容全面、完整，能够满足各种精度要求的海域面积量算技术规程。这既不利于保护海域权利人的合法权益，也不利于海域管理水平的提高。

由于地球是一个椭球体，在进行大区域面积量算时，必须要考虑椭球曲率、投影等问题[3]，因此，对于海域面积精确计算方法的研究，主要集中在考虑减小投影转换、地球曲率等引起的面积误差方面。冯纪军等[4]提出了基于高斯平面的坐标法、方格法和数点法等小区域海域面积便捷测算思路，李玉宝等[5]探讨了减少地球曲率和投影转换所引起的面积变形问题，吕慧玲[6]提出采用斜轴墨卡托投影的方法来解决跨区线路工程对面积计算精度的影响，林绿等[7]讨论了基于椭球面的不规则凸区域(经纬度)椭球面面积计算方法，王解先等[8]定量分析了高斯投影中央子午线与面积变形的对应关系，陈义兰等[9]从测量误差和面积计算误差两方面对海域面积测量总误差进行分析评价。为提高海域使用面积的量算精度，就需要充分考虑地球椭球体曲率等影响因子对面积计算的影响，以减小面积变形而带来的管理瓶颈和操作困难。

2 解析法海域面积计算

海域面积计算最简单方法是利用平面解析法原理，利用GIS软件的面积计算功能直接计算海域面积[10]。现行的海域测量、海域调查等规范中推荐的海域面积计算方法亦是解析法[2,11-12]。

根据解析法量算宗海面积的经典公式，可推导该计算方法的误差：

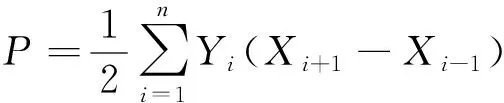
(1)

式中,P为宗海面积；(Xi,Yi)为界址点i的坐标；n为界址点个数。

假设界址点(Xi,Yi)的横纵坐标测量误差相对独立，根据误差传播定律可得：

(2)

式中,Mp为宗海面积P的中误差，MXi、MYi分别为Xi、Yi的中误差。

如假定MXi=MYi=M，则误差公式可简化：

(3)

令S(i+1,i-1)表示i+1与i-1两点间的距离，则：

(4)

可得：

(5)

按照《海域使用面积测量规范》和《海籍调查规范》规定：所测海域离岸20 km以内，测量误差优于±1 m；所测海域离岸20～50 km，测量误差优于±3 m；所测海域离岸50 km以外，测量误差优于±5 m[2,12]。

根据上述公式，以离岸20 km以内宗海测量为例，即中误差M=±1 m，计算出不同边长和不同边数正多边形的面积精度与相对精度的对应关系(表1)。

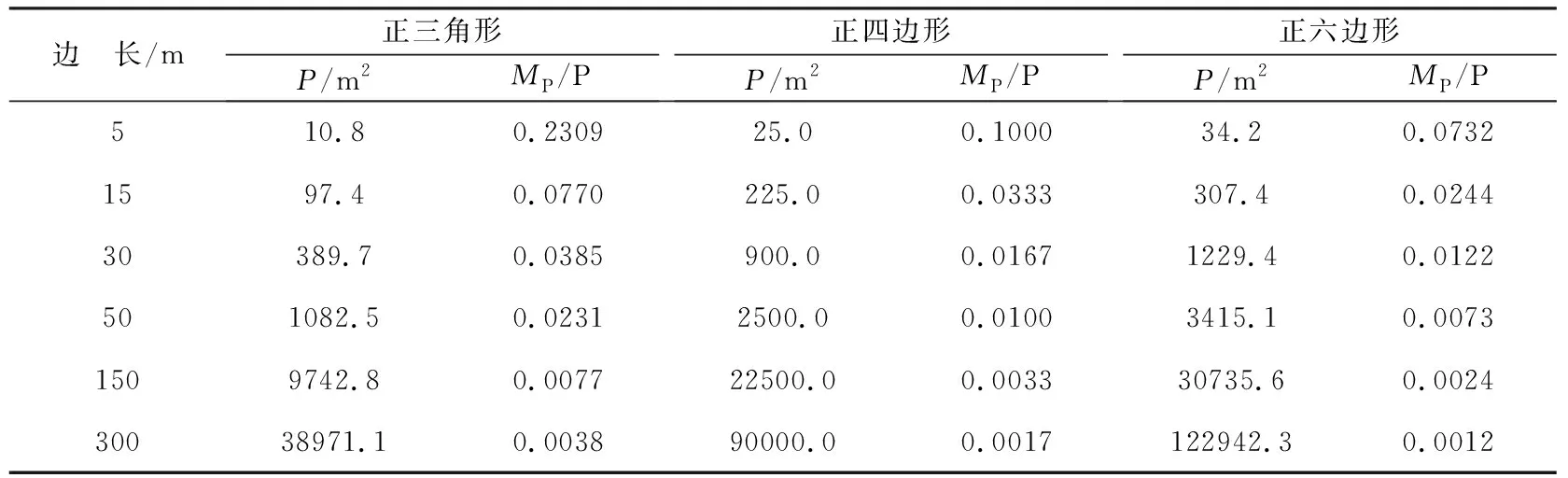
表1 正多边形面积量算精度与相对精度统计表Table 1 The calculated accuracy and the relative accuracy for the areas of different equilateral polygons

可见：解析法面积量算的相对精度(MP/P)，不但与界址点的坐标精度(点位误差)有关，而且与图形的大小和形状(边数和边长)有关。当面积和坐标中误差为定值时，界址点越密，面积量算的精度越高。此外，当认为界址点坐标中误差相同时，坐标解析法计算面积的中误差平方与多边形隔点距离平方和成正比。

此外，采用解析法计算海域面积，通常未考虑地球曲率等对面积计算的影响，只是根据测算区域界址点的高斯平面坐标进行计算。由于高斯-克吕格投影属于等角横轴切椭球圆柱投影，其特点是投影前后角度保持不变、面积微元形状保持相似性，但存在面积和长度变形，且随着距离中央子午线距离的加大，长度和面积的变形呈非线性加大，所以即使不考虑测量等误差，由此求得的海域面积也会与实际存在一定的差异，其结果将会给项目施工、海域综合管理带来误差和损失。

3 精度影响因子及其量化评价

地图投影的主要矛盾是曲面(地球椭球体或球体表面)和平面(地图平面)之间的矛盾[3]，在解决曲面和平面的转换过程中，必然产生变形(角度、面积和长度的变形)。海洋作为一个大面积区域，且地球表面又是一个不规则椭球体，采用传统基于平面的面积和距离测量方法，尤其是小比例尺海洋测量，就会由于地球曲率等影响而引起海域面积变形，甚至会严重影响测量和计算的精度。

通过对传统海域面积量算过程分析，对面积计算精度影响较大的因素主要有纬度差、投影方式与中央经线选择、椭球体参数及坐标转换等。

3.1 纬度差引起的面积变形

传统计算地球表面上的梯形面积，就是计算两条子午线和两条纬线为界所包围的椭球体表面积。按经典几何学方法，椭球体表面上介于经度L1至L2，纬度B0至(B1+B2)/2之间梯形面积A12的计算公式如下：

(6)

式中A12为梯形面积；b为椭球短半径；e为椭球体曲率半径。

假设某宗海权属线由4个界址点连成，各界址点分别为A(30°55′44.9978″N,122°14′5.2662″E)、B(30°57′45.4255″N,122°07′50.8174″E)、C(30°53′42.1776″N,122°10′50.4731″E)、D(30°55′0.7955″N,122°12′25.8155″E)，组成4条边界AB、BC、CD、DA，各点间纬度差见表2。

表2内插前宗海界址点纬度差统计表

在AB之间内插一点A′(30°56′45.2148″N,122°10′58.0403″E)，BC间内插一点B′(30°55′43.8036″N,122°9′20.6466″E)，依次类推，内插出C′(30°54′21.4863″N,122°11′38.1441″ E)、D′(30°55′22.8965″N,122°13′15.5406″E)点，使两点间纬度差变小，获得8个点的纬度差见表3。

表3内插后宗海界址点纬度差统计表Table 3 Latitude differences of boundary points after interpolation

根据公式(6)，可求得该宗海基于1954年北京坐标系下内插前面积为31 264 554.00 m2，内插后面积为31 264 934.00 m2，两者相差380 m2，即内插点后缩短了界址点间的距离，该宗海的椭球面积增大了380 m2，增大率在0.001 22%。因此，在实际生产过程中，为提高海域面积的量算精度，应根据项目需求和相关规范，选择适当的界址点距离。

3.2 投影方式与中央经线选择引起的面积变形

在国内基本比例尺地形图中，≥1/500 000的地形图均采用高斯-克吕格投影，又称“横轴墨卡托投影”，为一等角横切圆柱投影；小于1/500 000的地形图采用等角正轴圆锥投影，又称“兰伯特投影”；海区小于1/500 000的地形图多用等角正轴圆柱投影，又称“墨卡托投影”。不同的投影方式，由于其数理基础不同，必然会引起投影前后面积计算精度的不同。

在海域综合管理中使用的图件多采用高斯-克吕格投影，属正形投影，特点是等角投影，面积微元投影后能保持其形状的相似性，但存在长度及面积变形，且随着距离中央子午线距离的加大，长度及面积变形呈非线性增大。根据经典大地测量学理论，一般长度和面积的变形取值二次项[8，13]，其计算公式如下：

长度变形：

m=1+y2/2R2

(7)

面积变形：

m2=1+y2/R2

(8)

式中,m为高斯平面长度与椭球面长度之比；m2为高斯平面面积与椭球面面积之比；y为测区的平均横坐标；R为地球半径。

设北半球某宗海梯形小块的经度差dL与纬度差dB都是10′，下底纬度B=35°。将该宗海的高斯平面面积与其椭球面面积对比，求出高斯投影变形引起的面积变形。表4列出了面积变形与距中央经线经差的对应关系。图1显示了中央经线两侧随着距离中央经线距离的变化，其高斯平面面积的变形趋势。

表4高斯-克吕格投影引起的面积变形表Table 4 Area deformation Caused by the Gauss-Kruger Projection

图1 梯形面积变形与距离中央子线经差对应关系Fig.1 Relationship between the deformation of trapezium area and the distance of longitude to the central meridian

可以看出：高斯-克吕格投影后计算所得的面积大于实际椭球面面积，且随着梯形小块远离中央子午线，投影面积变形逐渐加大。

3.3 坐标转换引起的面积变形

由于不同坐标系采用的参考椭球体参数不一致，同一宗海面积会由于椭球体参数不一致引起面积变形。此外，由已知某一坐标下的界址点坐标计算其另一坐标系下的面积，亦会由于坐标系转换参数误差引起面积变形。由椭球体参数不一致引起的面积变形和坐标系转换参数误差引起的面积变形，可统称为坐标系转换引起的面积变形。

1)椭球体参数不一致引起的面积变形

采用GPS测量设备直接获取的界址点坐标信息一般是基于WGS84坐标系，要获得基于诸如西安80坐标系下的宗海面积，就需要进行坐标转换。我国西安80坐标系采用的是1975年国家参考椭球体，其长半轴为6 378 140 m；而WGS84坐标系采用WGS84椭球体，其长半轴为6 378 137 m。同一宗海在这两个坐标系下的面积亦有差异。表5列出了1:10 000比例尺下不同纬度的同一图幅在西安80坐标系和WGS84坐标系下的面积差异。

表5 1∶10 000下不同纬度西安80坐标系和WGS84坐标系图斑面积对比Table 5 Contrast of the area of the same map-sheet under different coordinate systems (the Xi`an-80 system and the WGS-84 system) at a 1∶10000 scale

可知：同一比例尺和坐标系下，随着纬度的升高，图幅的理论面积变小；在同一纬度下，西安80坐标系下的图幅面积较WGS84坐标系下的理论面积大，但随着纬度的升高，两者之间的差值变小。

2)坐标转换参数引起的面积变形

经典坐标转换常采用3个平移参数、3个旋转参数以及两坐标系尺度变化参数的七参数坐标转换法[14]。实际生产活动中，常采用4参数转换法，即通过旋转、平移和统一尺度来实现。其计算公式可表示为：

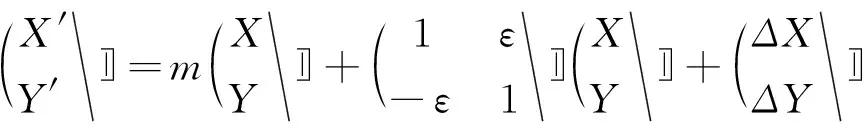
(9)

式中,(X′，Y′)为目标坐标系下的坐标；(X，Y)为源坐标系下的坐标；ΔX，ΔY为坐标平移参数；ε为旋转参数；m为两坐标系间的尺度因子。

将X′，Y′带入式(1)，可获得同一宗海转换前、后面积关系：

P′=(1+m2+2m+ε2)P

(10)

式中,P,P′分别为转换前、后的宗海面积。

根据公式(2)，可得坐标转换参数引起的相对面积变形：

(11)

式中，mP′,mm,mε分别表示面积变形误差、尺度因子误差和旋转因子误差。

假设某宗海4个界址点在西安80椭球面的坐标，利用4参数坐标转换法，获取其对应北京54坐标系下的坐标(表6)。再利用坐标高斯反算经典公式，分别求得该4个点对应6°带不同坐标系下的平面坐标(表7)。

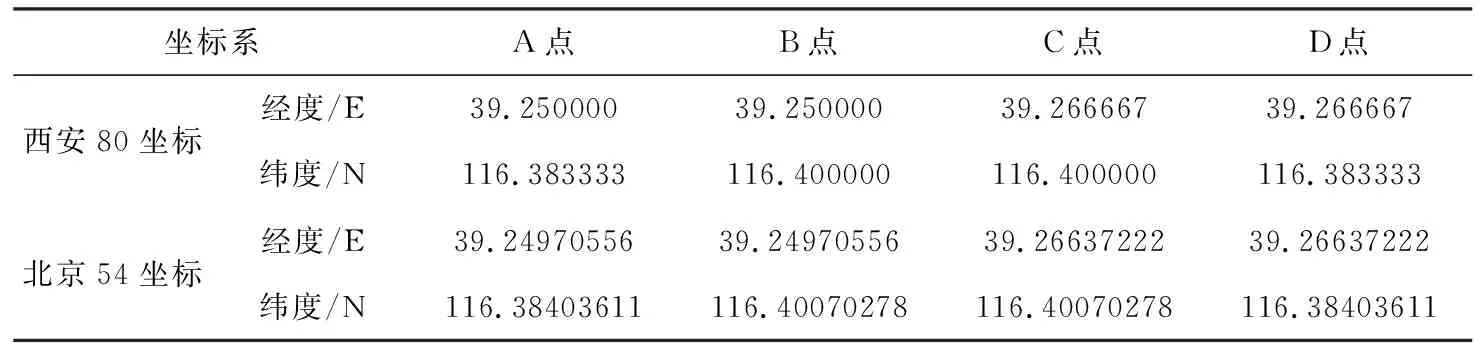
表6 已知4点的西安80坐标及北京54坐标Table 6 The Xi′an-80 coordinates and Beijing-54 coordinates of the four known points

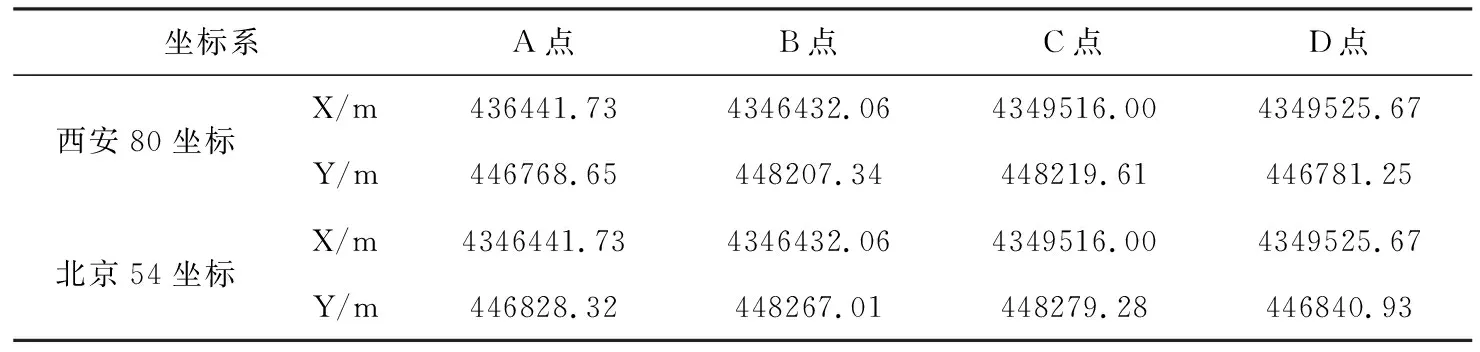
表7已知点的平面坐标信息(6°带投影)Table 7 Horizontal coordinates of the known points (6°)

由表7可知：该宗海在西安80椭球体上的面积为2 661 732.96 m2，在北京54椭球体上的面积为2 661 821.12 m2，两者相差88.16 m2，相对面积变形为0.000 033 12。因此，对于面积较小的宗海，坐标系转换参数引起的面积变形可以忽略不计，但对于大区域海域综合管理，该误差就应给予足够的重视。

4 提高海域面积计算精度的建议

1)权属线界址点的选择要合理。在实际生产活动中，对宗海权属线界址点的选择，应充分考虑海域综合管理的需要，从项目实际需要入手，遵守相关法规技术规程，按照比例尺及任务要求，选择恰当的界址点距离，以便从数据获取的角度提高面积计算精度，提供海域综合管理水平。

2)选择合适的投影带宽及中央经线。由于投影引起的扭曲变形随带宽不同而不同，与距离中央子午线的距离亦有一定的数量关系，在实际工作中，可首先根据面积求算精度要求，计算出其最大长度变形量，再根据面积变形公式，获取面积变形值，由此确定投影带宽。针对具体项目，可根据海籍区域大小，选取以用海范围中心相近的0.5°或1°整数倍经线为中央经线。

3)采用基于椭球面的海域面积计算方法。平面上计算宗海面积会受到中央子午线和投影面高程的影响，椭球面上的面积有助于在大范围内统一面积计量，有效减小地图投影中产生的扭曲变形。在计算面积时，要保证面积计算结果更真实地反映用海区的真实面积，可考虑采用基于椭球面的等面积投影计算方法。

参考文献：

[1] 刘赐贵.管好海域资源构建生态文明[N/OL]. [2013-07-10]http://www.gove.cn/gzdt/2012-3/congtent_2090840.htm.

[2] HY/T 124-2009. 海籍调查规范[S]. 北京：中国标准出版社，2009.

[3] 王进华，张鹰，王艳君. 关于海域面积精确计算的若干问题探讨[J]. 海洋技术，2002，21(1)：64-67.

[4] 冯纪军，戴冉，朱金善. 海域面积测算的几种方法[J]. 大连海事大学学报，2007，33(增):100-103.

[5] 李玉宝，曹智翔. 顾及地球曲率的面积计算问题[J]. 重庆交通学院学报，2007，26(2)：152-154.

[6] 吕慧玲. 斜轴墨卡托投影方法在郑西客专中的应用[J]. 测绘信息与工程，2009，34(1)：26-28.

[7] 林绿，马劲松. 地球椭球面上区域面积的算法研究[J]. 测绘通报，2007，(6)：8-10.

[8] 王解先，俞振武. 高斯投影引起的面积计算误差[J]. 测绘通报，2003，(4)：5-6.

[9] 陈义兰，周兴华，吴永亭. 海域使用面积测量精度的探讨[J]. 海岸工程，2012，31(3)：40-44.

[10] 李巧稚. 海域使用测量关键问题探讨[J]. 海洋信息，2005，(3)：8-11.

[11] HY070-2003. 海域使用面积测量规范[S].北京：中国标准出版社，2003.

[12] HY/T 124-2009. 海域调查规范[S].北京：中国标准出版社，2009.

[13] 党亚民，成英燕，吴秀娟，等. 不同坐标系图斑理论面积计算研究[J]. 测绘科学，2005，30(6)：23-25.

[14] 程效军，顾孝烈. 解析法土地面积量算及精度分析[J]. 城市勘测，1994，(4)：4-7.