利用Mathematica 研究纱窗网孔的Fraunhofer 衍射

杨 坤

(沈阳化工大学 数理系，辽宁 沈阳 110142)

物理学是与日常生活关系最密切的学科，很多物理现象都可以在生活中观察到.譬如:很多人都曾在楼上透过纱窗观察远处的灯光，看到了纱窗网孔的衍射现象.但是，由于数学推导上的困难，到目前为止，还没有人给出该现象的理论解释.本文借助Mathematica 软件，利用基尔霍夫衍射理论，推导出由矩形孔构成的2 行×2 列、4行×2 列、2 行×4 列、4 行×4 列等纱窗网孔的Fraunhofer 衍射相对衍射强度公式，并在此基础上归纳推广，得到由2n行×2m列矩形孔构成的纱窗网孔的Fraunhofer 衍射相对衍射强度通式.绘制出不同数目矩形孔构成的纱窗网孔的几种典型衍射图样及对应的相对光强三维立体图，更加真实、精确、简便地再现了生活中看到的不同数目矩形孔构成的纱窗网孔的Fraunhofer(夫琅禾费)衍射现象，对深刻理解不同数目矩形孔构成的纱窗网孔的Fraunhofer 衍射现象具有重要意义.

1 纱窗网孔的Fraunhofer 衍射光强

任意孔的Fraunhofer 衍射的基尔霍夫衍射理论公式为［1－2］:

其中，UP(X，Y)是在屏幕上任意点p(X，Y)的电磁波函数的值，r 是孔的某一微小面元至接收屏上的点p(X，Y，Z)的距离，k 是光的波矢值，C 是与光源和观察点位置相关的一些物理量来确定的复常数.

图1 为矩形4 孔与屏上各点的坐标表示.由图1 可知:

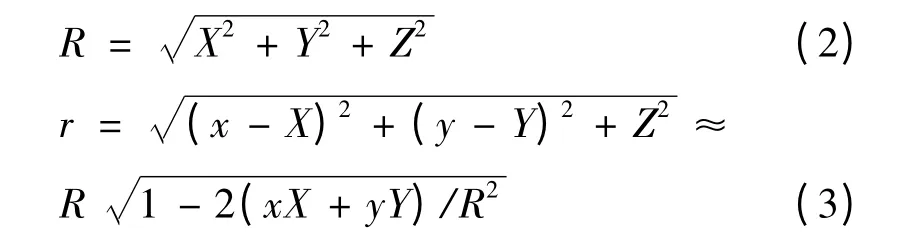
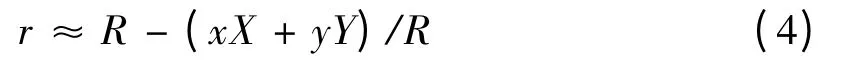
把式(4)代入到式(1)可得:

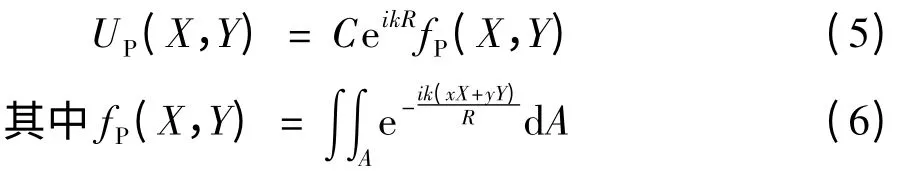
在屏幕上任意点(X，Y)的光的强度为:

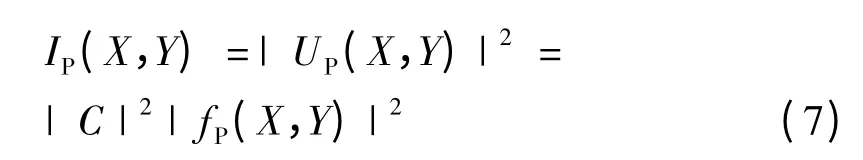
在屏幕中央点(0，0)上的光的强度为:

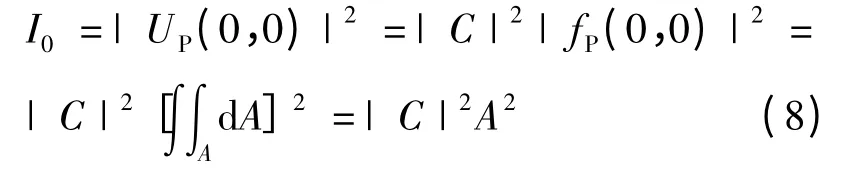
在屏幕上任意点(X，Y)的光的相对强度为［3－4］:

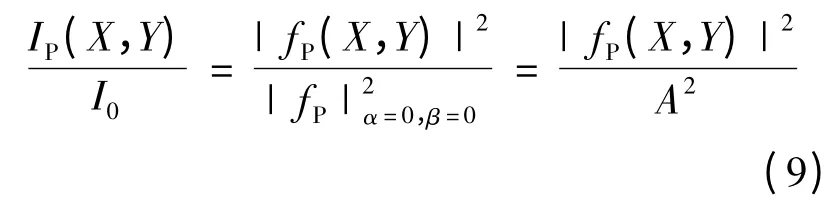
对于矩形孔构成的2 行×2 列的纱窗网孔的4 孔(如图1 所示)，根据图1 和式(6)可得:

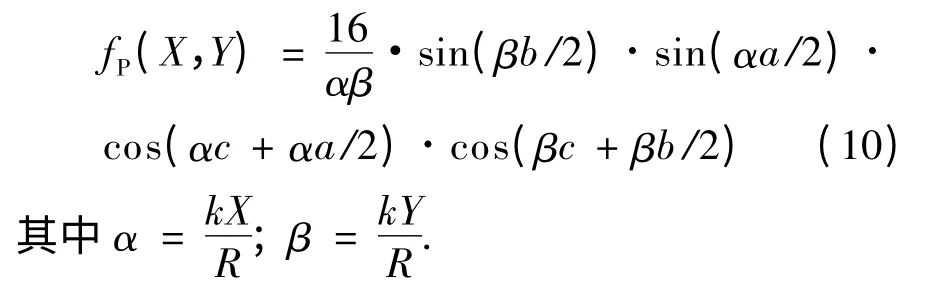
由图1可得:A =4ab，式(10)代入式(9)，经化简可得:

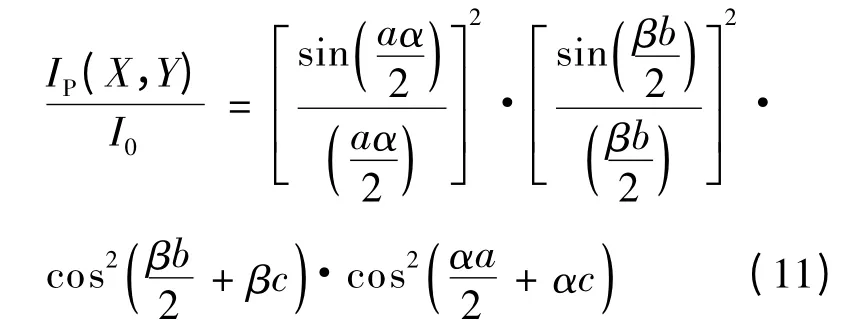
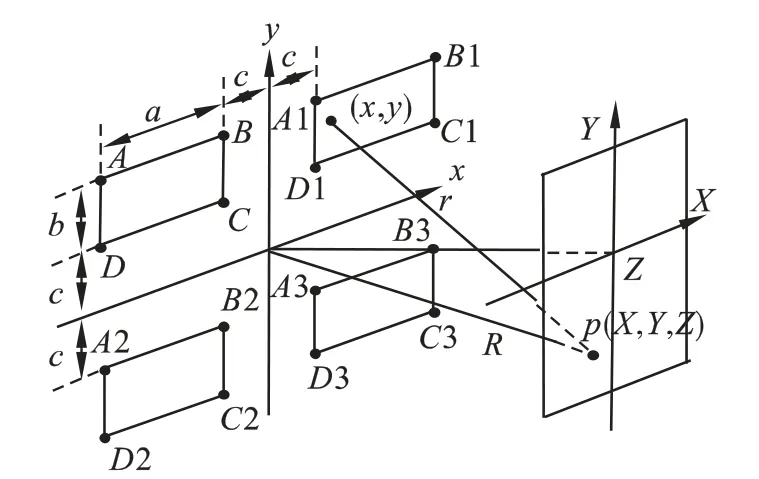
图1 矩形4 孔与屏上各点的坐标表示Fig.1 Four rectangular holes and the screen coordinates of the points indicated

图2 为4 行×2 列矩形8 孔与屏上各点的位置示意图.

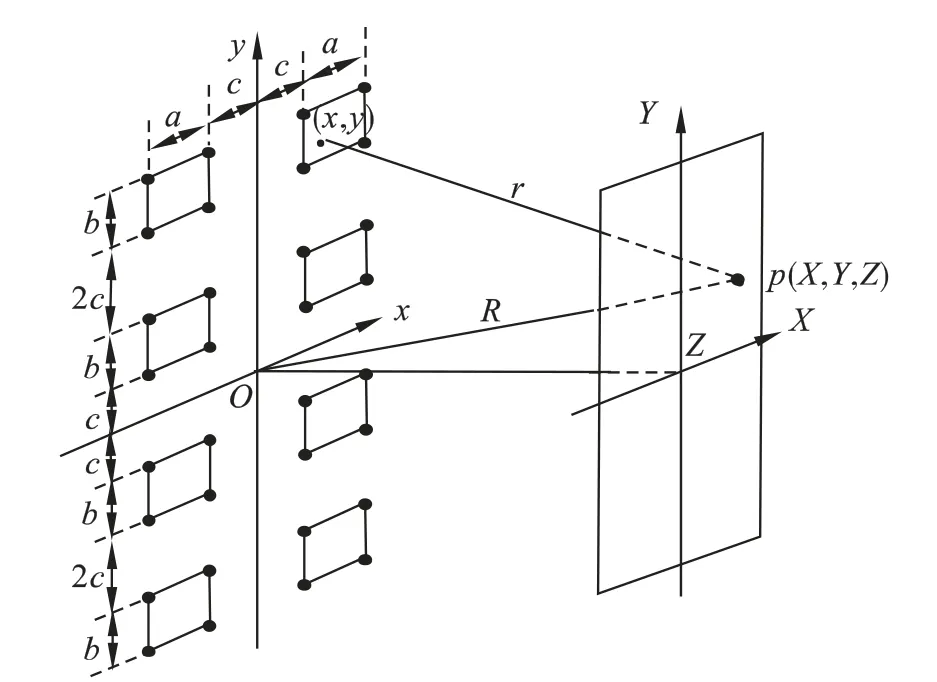
图2 4 行×2 列矩形孔构成的纱窗网与屏上各点的位置示意图Fig.2 4 ×2 rows of rectangular holes of the window screen and screen the schematic diagram

对于矩形孔构成的4 行×2 列的纱窗网孔的8 孔(如图2 所示)，仿照图1 写出图2 各矩形孔的各点坐标，再利用式(6)可得:

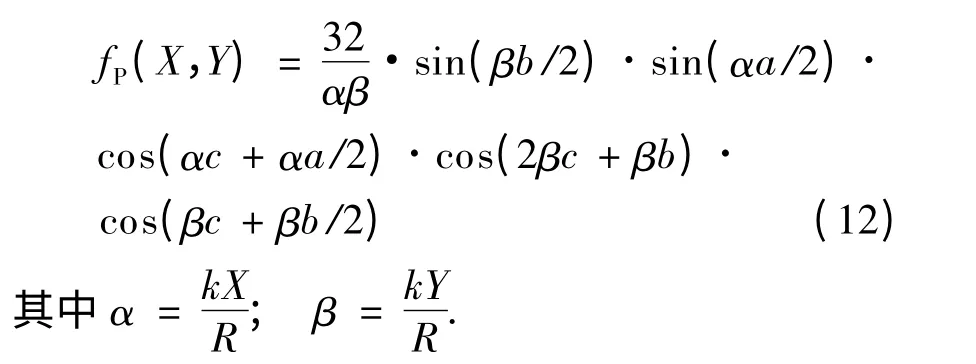
由图2 可得:A =8ab，式(12)代入式(9)，经化简可得:

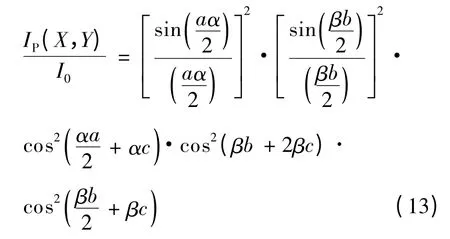
图3为2 行×4 列矩形8 孔与屏上各点的位置示意图.

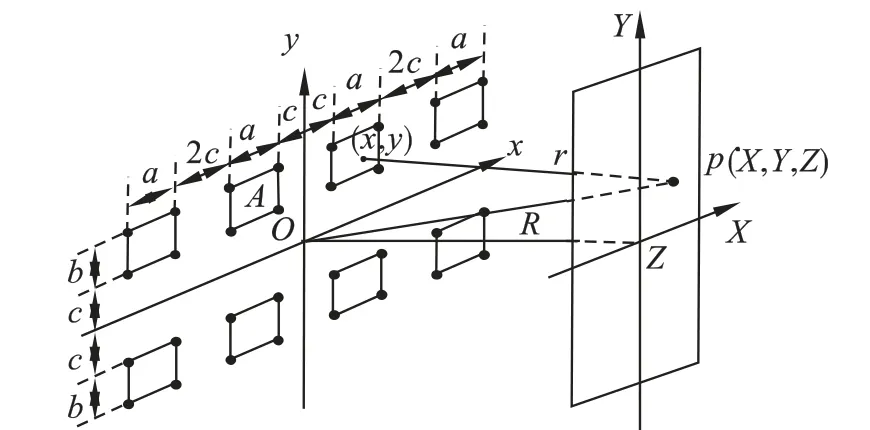
图3 2 行×4 列矩形孔构成的纱窗网与屏上各点的位置示意图Fig.3 2 ×4 rows of rectangular holes of the window screen and screen the schematic diagram

对于矩形孔构成的2 行× 4 列的纱窗网孔的8 孔(如图3 所示)，仿照图1 写出图3 各矩形孔的各点坐标，再利用式(6)可得:

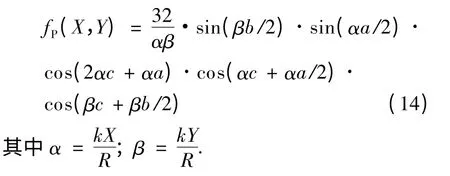
由图3 可得:A=8ab，式(14)代入式(9)，经化简可得:

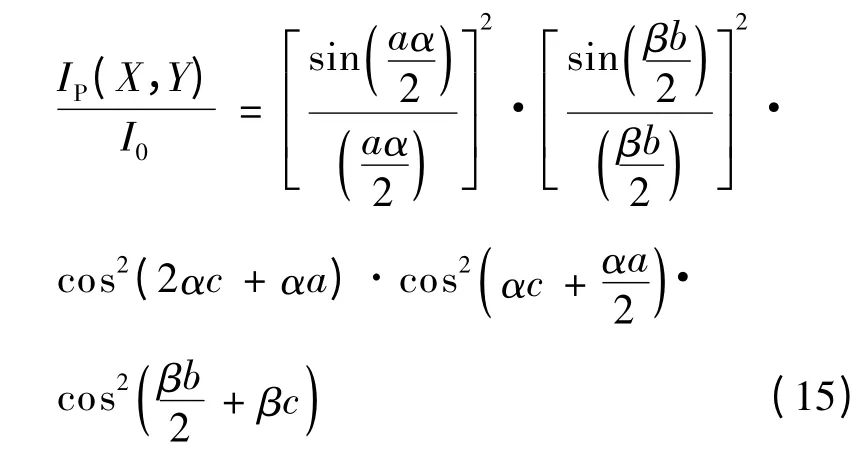
图4 为4 行×4 列矩形孔构成的窗纱网与屏上各点的位置示意图.

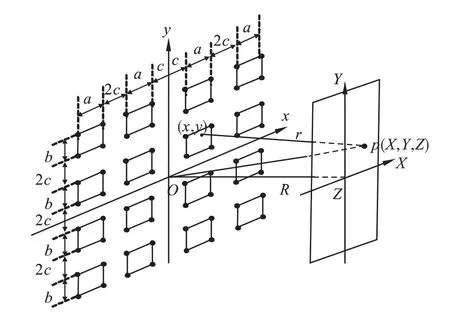
图4 4 行×4 列矩形孔构成的纱窗网与屏上各点的位置示意图Fig.4 4 ×4 rows of rectangular holes of the window screen and screen the schematic diagram

对于矩形孔构成的4 行× 4 列的纱窗网孔的16 孔(如图4 所示)，仿照图1 写出图4 各矩形孔的各点坐标，再利用式(6)可得:

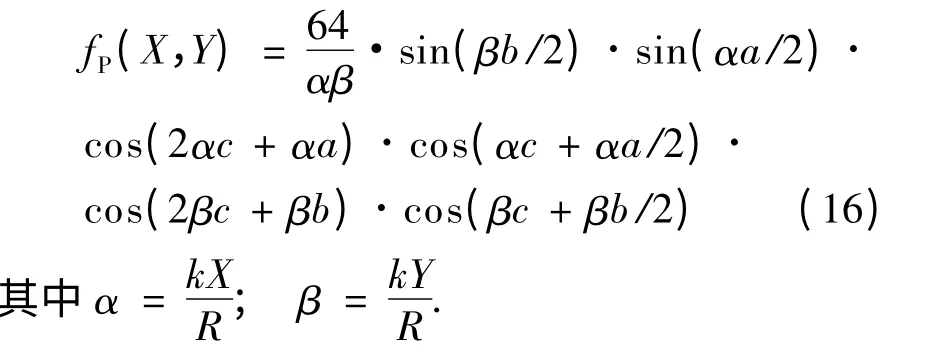
由图4 可得:A=16ab，式(16)代入式(9)，经化简可得:

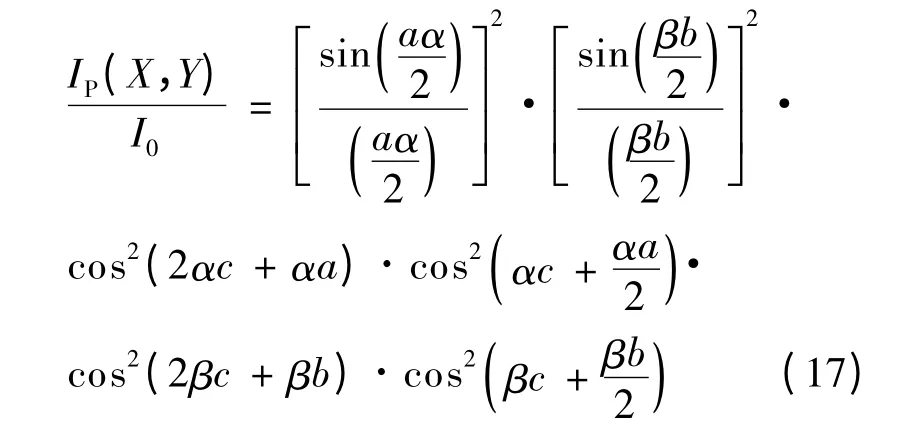
图5 为2n行×2m列矩形孔构成的窗纱网与屏上各点位置示意图.

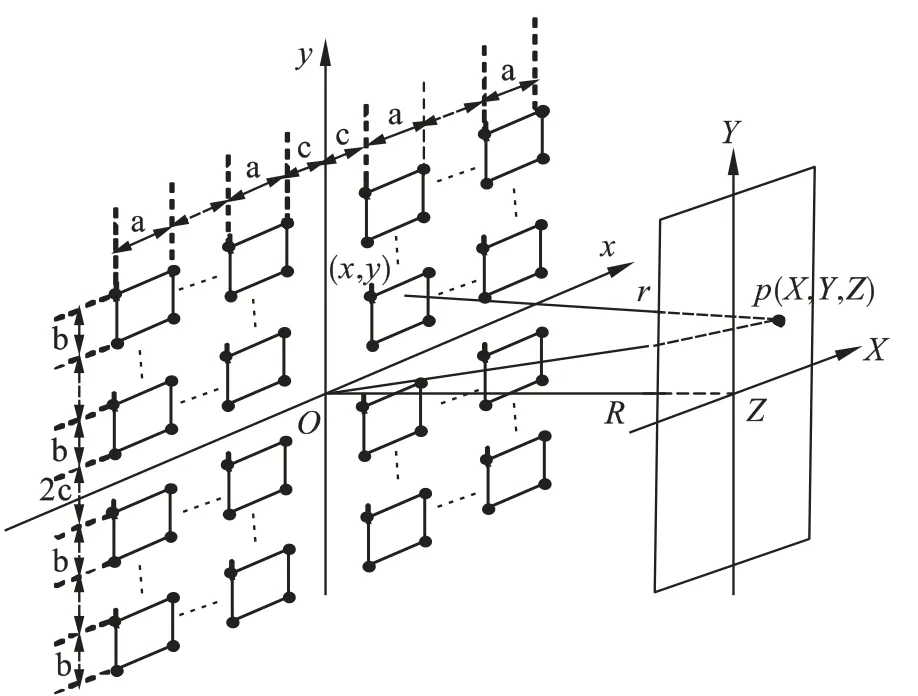
图5 2n 行×2m 列矩形孔构成的纱窗网与屏上各点的位置示意图Fig.5 2n ×2m rows of rectangular holes of the window screen and screen the schematic diagram

对于矩形孔构成的2n行×2m列的纱窗网孔的2n×2m个孔(如图5 所示)，由式(10)、(12)、(14)、(16)归纳推理可得:

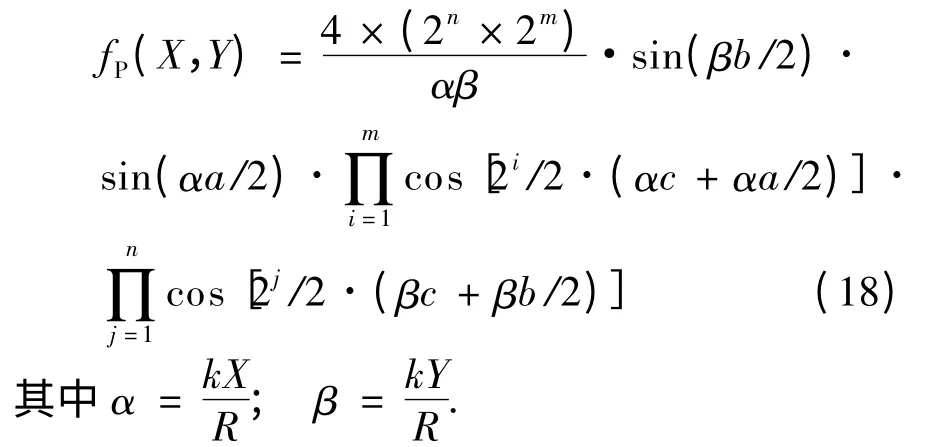
由图5 可得:A=(2n× 2m)ab，式(18)代入式(9)，经化简可得:

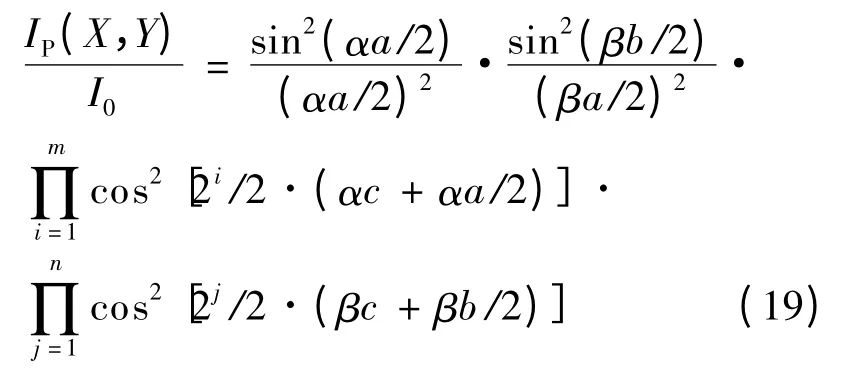
2 不同数目矩形孔构成的纱窗网孔在接 收屏上的Fr a unhofer 衍射模拟［5］

根据式(19)，利用Mathematica 软件中DensityPlot 函数，模拟绘制不同数目矩形孔构成的纱窗网孔在接收屏上的Fraunhofer 衍射图样，用Plot3D 绘制接收屏上相对光强三维立体图如表1 所示.

表1 不同数目矩形孔构成的纱窗网孔在接收屏上的Fraunhofer 衍射图样及对应的相对光强三维立体图Table 1 Different number of rectangular holes of screen mesh in the receiving screen Fraunhofer diffraction pattern and the corresponding relative intensity of 3D map

续表

由表1 的(6)、(7)、(8)、(9)图可知:纱窗网孔Fraunhofer 衍射图样的主要结构是中间较粗的十字线形状，旁边还有一些细的横的与竖的亮线，这些亮线在交叉的地方亮度增大.这与透过纱窗观察远处灯光看到的结果是一致的.从对应的相对光强三维立体图也可以看出:大小、孔间隔均相同的矩形孔构成的纱窗网孔，随矩形孔数目增多，其主极大所包含的次极大数目变多，各级次极大衍射明纹强度明显变尖变细.对数目、孔大小、分布均相同的矩形孔构成的纱窗网孔，随相邻矩形孔间隔增大，其主极大所包含的次极大数目变多，各级衍射明条纹强度明显比同一级明纹强度变细变尖，次极大间隔变小，各孔的多光束干涉现象越来越明显，如表1 中图(1)、(10);对数目、分布、孔间隔均相同的矩形孔构成的纱窗网孔，随矩形孔变大，其主极大所包含的次极大数目不变，但各级衍射明条纹强度明显比同一级明纹强度变小，次极大间隔变小，各孔的多光束干涉现象明显减弱，如表1 中图(1)、(11).

根据表1 可知:欲找出一定数目矩形孔或方形孔构成的纱窗网孔与Fraunhofer 衍射图样的内在规律，可以通过改变各参数值，得到不同条件下纱窗网孔在屏上的Fraunhofer 衍射图样及相应的相对光强三维立体图，有针对性地总结出其遵循的规律.

3 结论

对于由2n行×2m列的矩形孔构成的纱窗网孔的Fraunhofer 衍射相对衍射强度通式，通过改变m、n、a、b、c 参数值，就可以绘制出对应数目矩形孔构成的纱窗网孔的衍射图样及相应的相对光强三维立体图，更加真实、精确、简便地再现了该数目矩形孔构成的纱窗网孔的Fraunhofer(夫琅禾费)衍射现象.事实上，这些实验现象用实验方法也都可以观察到，但成本要比用这种方法高得多.所以，该方法是研究这类问题的简单有效方法.

［1］马科斯·玻恩，埃米尔·沃尔夫.光学原理.上册［M］.北京:电子工业出版社，2005:342－428.

［2］EUGENE HECHT.Optics［M］.4thed.New York:Addison-Wesley，2002:447－464.

［3］杨坤，成泰民，葛崇员.矩形孔和圆孔构成的双孔Fraunhofer 衍射图样模拟［J］.沈阳师范大学学报(自然科学版)，2012，30(1):36－39.

［4］杨坤，成泰民.不同三角形孔和矩形孔构成的双孔Fraunhofer 衍射图样模拟［J］.曲阜师范大学学报(自然科学版)，2012，38(2):64－68.

［5］张韵华，王新茂.Mathematica7 实用教程［M］.合肥:中国科学技术大学出版社，2011:215－217.