基于压缩感知的无线传感器网络节点定位算法
赵春晖,许云龙,黄 辉
(哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150001)
无线传感器网络(wireless sensor network,WSN)是一种全新的信息获取平台,可以在广泛的应用领域内实现复杂的大范围监测和追踪等任务.其中,网络节点自身定位是一个关键的问题,它是确定网络路由协议[1]、实现目标定位与追踪等的前提.然而无线传感器网络是由廉价的能量有限的感知器组成,只有少部分的感知器节点知道自身的位置.因此,通过这些少量的位置信息去准确、有效、快速地定位所有节点的位置已经成为研究热点.
目前,已有许多算法来解决节点自身定位问题.但是,大多数算法通常只适合某类应用,而不是通用的算法.因此,为了保证算法的可靠性、有效性及通用性,解决定位问题必须满足以下3个条件:①依靠节点自身的通信设备来进行节点定位,可以有效地降低定位的成本;②存在着少量的信标节点,可以有效地提升定位精度,保证算法的有效性和可靠性;③节点不需要与信标节点直接通信,可以有效地降低节点传输距离的要求及节点的通信能耗,同时保证算法的通用性.
无线传感器网络定位方法分为基于测距的(range-based)和无需测距的(range-free)定位两类.典型的测距定位算法主要有:基于测距的定位通过测量距离进行定位,如接收信号强度(RSSI)[2]、信号传 播时间(TOA,TDOA)[3-4]、接收信号方向(AOA)[5]等.基于测距的定位一般精度较高,但是需要额外的测距设备.典型的距离无关定位算法主要有质心算法(Centroid)[6-8]、APIT[9]、Diffusion[10]、LSVM[11]、LSRC[12]和WHEEL[13]等.显然,基于测距的算法需要与信标节点直接通信,明显不满足条件③,而无需测距的算法也大部分不符合上述3个条件.已知满足以上条件的比较有代表性的算法有:Diffusion、LSVM 和LSRC算法,文献[11]已经证明了LSVM 算法比Diffusion算法性能优越很多,因此本文将以LSVM 算法和LSRC 算法作为对比算法.
LSVM、LSRC算法将分类的原理应用到节点定位中,必须建立分类模型,它们存在以下三个缺点:①在分类模型中,二者均是利用二叉树分类结构进行定位,但是其在估计节点坐标时,是把x,y 轴坐标分开估计的,没有更好地体现出节点之间连通信息的空间特征,因此定位精度不高.②分类模型的建立过程相当复杂并且依赖信标节点的位置信息,任意一个信标节点的位置信息不正确,都将导致LSVM 和LSRC 算法的失效.③在LSVM 算法中需要选择一个信标节点当作头信标结点去建立分类模型,将使这个头信标节点消耗较大,这对能耗要求较高的传感器网络是很不利的.
本文提出了两种新的节点定位算法——基于压缩感知的无线传感器网络节点定位算法(node localization algorithm based on compressed sensing,NLCS)和 改 进的 NLCS(improved NLCS,INLCS).NLCS算法是一种无需测距的定位算法,其通过压缩感知(compressed sensing,CS)[14]算法得到目标节点与信标节点之间的相关程度,并由相关程度去决定信标节点对目标节点定位的权值大小,最后得出目标节点的估计位置.
相比于LSVM、LSRC算法,NLCS算法有以下几个优势:①在估计节点的位置时,利用的是质心算法,充分体现了目标节点与信标节点的空间相关性,从而提升了算法的定位精度.②在节点定位过程中,计算信标节点对普通节点的权值影响时,并不使用信标节点的位置,而仅仅使用节点间的连通信息,因此即使存在少数信标节点的位置不正确,也不会影响信标节点得到的采样原子,这样对于大多数目标节点的定位并不会产生影响.③由于采样字典是由各个信标节点自身得到的采样原子组成,这将更好地平衡网络中各节点的能耗.
此外,针对LSVM、LSRC 和NLCS算法中,计算连通信息均采用的是最小跳数,这样会导致目标节点被信标节点不准确地描述,从而影响定位算法的精度,提出了伪跳数的概念,来进一步改进NLCS算法,得到INLCS算法.
1 CS 和Centroid
CS理论表明,如果信号是可压缩的或在某个变换域是稀疏的,就可以通过一个满足约束等距性条件(restricted isometry property,RIP)[15]的观测矩阵将变换所得的高维信号投影成一个低维信号,最后通过求解一个优化问题以高概率重构出原信号.在CS模型中先对信号f 进行稀疏变换,如下式所示:
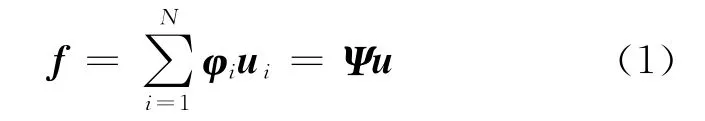
式中,u,f 是N×1的向量;Ψ 是N×N的稀疏矩阵.如果Ψ 是满秩的,且系数向量u中仅有k(k≪N)个非零系数,则认为信号u 在Ψ 上k 稀疏的.之后通过观测矩阵Φ 得到信号f的观测值y如下:
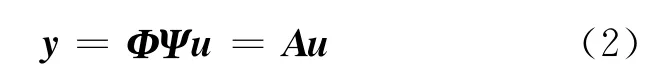
式中,y 是M×1的观测向量;Φ 是M×N(M≪N)的观测矩阵,令A=ΦΨ,它为CS信息算子.上述稀疏求解问题可以表示为下式:
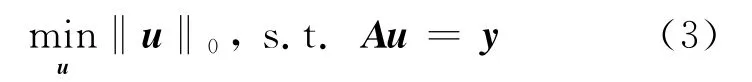
由于上式l0-norm 问题是一个NP难题,无法直接求解.由于u 是稀疏的,因此可以把式(3)的问题转化为l1-norm[16]或l2-norm[17]优化问题,得到其稀疏解.
Centroid的主要思想是:未知节点以所有在其通信范围内的信标节点的几何质心作为自己的估计位置.具体定位过程为:信标节点周期性向邻居节点广播一个信标信号,该信标信号中包含有信标节点自身的ID 和位置信息,当未知节点在一段时间侦听到来自信标节点的信标信号数量超过某一预设的门限值时,就认为该信标节点是未知节点的邻居节点,未知节点就把自己的位置确定为与之相邻的所有信标节点组成的多边形的质心,显然,Centroid算法无法满足前言第二段中的条件③.
本文借鉴Centroid的思想,通过信标节点的连通信息线性分解普通节点的连通信息,来挖掘普通节点和所有信标节点的相关程度,基于此决定每个信标节点对质心坐标的权值大小,最后通过加权Centroid算法定位普通节点的坐标.
2 基于压缩感知的无线传感器网络节点定位算法(NLCS)
2.1 传感器网络模型
假设在[0,X]×[0,Y](X,Y>0)区域内,存在N 个节点,分别用S1,S2,…,SN表示,其中k(k<N)个节点的位置已知,称这k 个节点S1,S2,…,Sk为信标节点,称其余N-k 个位置未知节点SN-k+1,…,SN-k+i,…,SN为普通节点.假设所有的节点都有相同的通信半径R,如果一个节点处在另一个节点的通信半径R 之内可以直接通信,称之为单跳.用h(Si,Sj)(i,j=1,2,…,N)表示节点Si和Sj之间的最短跳数.文中假设存在k(k<N)个信标节点,它们知道自己的位置和到达对方的最佳路径.需要设计一个分布式算法,通过这k 个节点去估计其余N-k 个节点的位置.现有的很多定位技术要求这N-k 个节点的通信范围内,必须有一些或全部单跳信标节点.而本文的算法则没有这样的要求,只需要每个节点可以与信标节点通信,无论其是通过多跳路径还是单跳路径.因此,文中提出的方法,将更适用于传感器网络的节点自定位.
2.2 定位算法原理
假设[x(Si),y(Si)]为第i个信标节点的地理位 置,φi=[h(Si,S1),h(Si,S2),…,h(Si,Sk)]T∈Rk×1(i=1,2,…,k)为第i个信标节点与所有k 个信标节点的连通信息,其中,h(Si,Si)=0,即节点到自身的跳数为0.将这些信标节点的连通信息组合成稀疏变换矩阵Ψ:
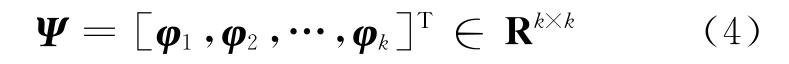
同理,fj=[h(Sj,S1),h(Sj,S2),…,h(Sj,Sk)]T(j=N-k+1,…,N)表示第j个普通节点与所有k 个信标节点的连通信息.依据稀疏变换基Ψ,fj能够被稀疏分解为:
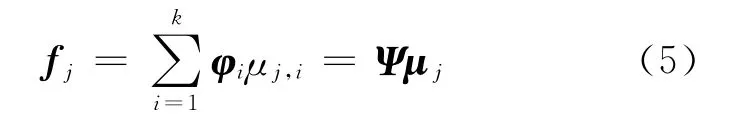
式中,μj=(μj,1,…,μj,i,…,μj,k)T是一个列向量,μj,i是第j 个普通节点在稀疏分解基下与第i 个信标节点之间的相关程度.通常两个节点位置越接近,则它们的相关程度可能越大,反之将很小,甚至为0.并且,第j个普通节点的连通信息的主要成分将被靠近其的少数几个信标节点的连通信息所描述,它们的系数将较大,而远离第j个普通节点的大多数信标节点,它们的系数都接近于0或者等于0,这也就是说,μj是稀疏的.因此,通过CS可以准确地重构出这些相关系数.
依据式(3),CS信息算子A 和压缩连通信息yj可以分别表示为:
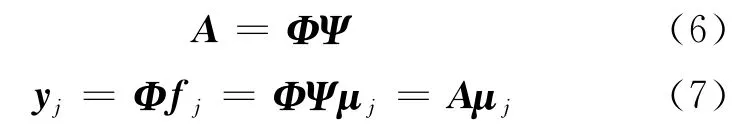
通过CS理论,式(7)中μj将被准确地重构,并利用μj得到第i 个信标节点对第j 个普通节点的权值ωi,j,其表达式如下:
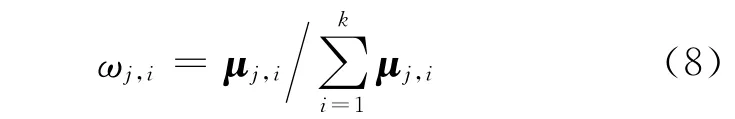
最后,通过加权质心算法可以得到第j 个普通节点的估计位置[x(Sj),y(Sj)]为
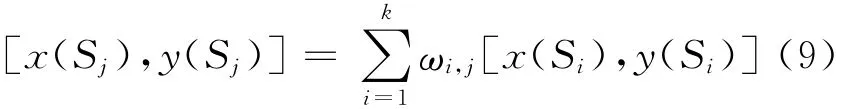
2.3 协 议
根据以上所述,定位一个普通节点Sj的关键是通过压缩感知算法得到第j 个普通节点和k 个信标节点的相关程度.普通节点的定位协议可以分为三个阶段:
(1)数据收集阶段.首先使用典型的泛洪扩散协议,使网络中所有节点获得距离信标节点的最小跳数.每个信标节点向邻居节点发送一个消息Hello{ID,h},ID 包括该信标节点的标号和其地理位置,h为跳数,其初始值为1.此后,为了防止消息的无限循环,各个接收节点只记录到每个信标节点的最小跳数,忽略来自同一信标节点的大跳数信息,然后将跳数值加1,并转发给邻居节点.通过这一机制,使网络中的所有节点知道到每一个信标节点的最小跳数.
(2)广播阶段.第i个信标节点根据收到连通信息φi,对其进行压缩,得到采样字典A的原子Ai.然后向整个网络广播Ai.
(3)定位阶段.第j 个普通节点首先对自身到所有信标节点的连通信息fj,通过测量矩阵Φ进行压缩,然后根据接收到的采样字典A,并结合压缩感知算法,得到其与所有信标节点的相关程度μj,最后使用权值质心算法计算其坐标,得到其估计位置[x(Sj),y(Sj)].
NLCS算法收集的连通信息均是各个节点到信标节点的最小跳数,它们均为整数,这样在较为邻近的节点的连通信息就非常相似,因此,可能造成由所有信标节点的连通信息组成的稀疏变换基,对目标节点的连通信息进行分解时,得到的稀疏分解结果不够准确.例如有两个信标节点接近于目标节点,这两个信标节点的连通信息很相近,目标节点就无法判断出跟哪个更接近,这样就可能会出现最接近目标节点的信标节点的相关程度可能不会是最大的,而较接近的将变成最大相关程度的信标节点.因此,它得到的稀疏分解肯定不是最优的,这样由它得到的目标节点的定位精度也将受到影响.
3 改进的NLCS(INLCS)
3.1 改进原理
NLCS、LSRC和LSVM 算法中,由于各个节点到信标节点的跳数值只能是整数,这样它们彼此之间的跳数与它们之间距离的关系将不是很准确,从而使得连通关系与距离的对应关系不够准确,进而影响稀疏分解的准确性.基于此,文中提出了伪跳数的概念,来得到更精确的节点连通关系.伪跳数是使用信号强度来确定彼此之间的跳数关系,能使节点间的跳数与距离更好地对应,使连通信息更加准确.
伪跳数的获取:每个节点发送一个信号强度为P0的信号,这样该节点的一跳节点将会接收到该信号,接收到的信号强度为Pi,之后各个一跳节点把该信号接收强度Pi反馈给这个节点,这样该节点就得到了所有一跳节点信号接收强度.由于噪声的存在,两个邻居节点得到的彼此接收信号强度不一样,因此可以取这两个彼此的信号接收强度值的平均值作为这两个节点之间的信号接收强度值.之后利用泛洪扩散协议,把每个节点得到的信号接收强度值中的最小值和最大值在网络中进行信息交换,得到整个网络中所有节点中的信号接收强度的最大值Pmax与最小值Pmin.之后每个节点利用这些信号强度接收值来计算到其一跳节点的伪跳数,伪跳数计算公式如下:

式中,Phopi,j为第i 个节点与第j 个节点的伪跳数,且第i个节点与第j 个节点为邻居节点,Pi,j为两个节点之间的信号接收强度值.
基于上述原理,可以得到各个节点到其邻居节点的伪跳数,之后利用这些伪跳数来得到各个节点到所有信标节点的连通信息.由于连通信息是通过伪跳数取得,因此每个节点到所有信标节点的连通信息将是非常准确的.在INLCS 算法中,只需要对NLCS算法中的数据收集阶段进行修改,得到各个节点到所有信标节点的更准确的连通信息即可,修改的数据收集阶段协议如下.
首先获取每个节点与其一跳节点之间的伪跳数.之后使用典型的泛洪扩散协议,使网络中所有节点获得距离信标节点的最小伪跳数信息.每个信标节点向邻居节点发送一个消息Hello{ID,h},ID 包括该信标节点的标号和其地理位置,h为其到各个邻居节点的伪跳数信息集合.此后,为了防止消息的无限循环,各个接收节点只记录到每个信标节点的最小伪跳数值,忽略来自同一信标节点的大伪跳数值,其中,两个节点间的伪跳数值为连通两个节点的路径上伪跳数的和值.然后节点把到每个信标节点的最小伪跳数值和信标节点ID 转发给邻居节点.通过这一机制,使网络中的所有节点知道到每一个信标节点的最小伪跳数值.最后把这些最小伪跳数值组成每个节点的连通信息.
3.2 算法的有效性分析与对比
假设有1 000个传感器节点随机分布于大小为100m×100m的区域内,其中信标节点的比例为5%,节点通信半径R=6m,随机选取其中一个普通节点,仿真出的该节点与信标节点的相关系数示意图如图1所示.

图1 节点与目标节点的相关系数示意图Fig.1 Schematic of the correlation coefficient between the node and beacon nodes
由图1中可以发现,相关系数较大的项,总是对应那些在几何位置上比较靠近目标节点的信标节点,而大部分离目标节点比较远的信标节点的相关系数都等于0.此外,从图1 中还可以看出,相关系数较大的节点非常少,大部分节点的相关系数为0或者接近于0,即相关系数向量是稀疏的.因此,通过压缩感知算法能够准确地重构出普通节点和信标节点的相关度,进而较好地估计出普通节点的位置.
此外,通过对比图1a和图1b 可以看出,在INLCS算法中最靠近目标节点的信标节点的相关程度远大于其他信标节点,而在NLCS 算法下,离目标节点最近的信标节点所得的相关程度与离目标节点较远的几个信标节点的相关程度值差不多,通过对比两个分解图可以看出在INLCS算法下的稀疏分解比NLCS 更准确.因此,INLCS算法的定位精度将高于NLCS.
3.3 算法的能量分析与对比
从上面的分析可知,相比于NLCS 算法,INLCS算法中在数据收集阶段需要每个节点获取彼此之间的伪跳数,这个过程会带来更多的能量消耗,而其他的过程是一样的.但是,通过上节的算法分析可以看出,相比于NLCS 算法,INLCS算法提高了稀疏分解的准确性,提高了算法的定位精度,并且下一节的实验结果也表明,相比较于NLCS算法来说,INLCS算法无论是平均定位误差还是定位误差标准差均得到了进一步的改善,也就是说INLCS算法的定位性能要优于NLCS算法.因此,在实际应用中,需要均衡地考虑能量消耗和定位性能来选择哪种算法更适合.
4 实验结果与分析
假设有1 000个传感器节点随机分布于大小为100m×100m的区域内,其中信标节点的比例分别为5%,10%,15%,20%,同时取两个不同的通信半径R=6m 和R=12m,得到了如图2所示的INLCS、NLCS、LSRC、LSVM 算法的定位性能对比图.
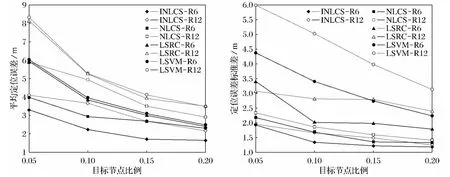
图2 4种算法的定位性能对比Fig.2 Comparison of positioning performance of the four algorithms
由图2a可以看出INLCS算法有最小的平均定位误 差,NLCS 次 之,LSRC 和LSVM 相 对 较差.在R=12m 时,NLCS算法的平均定位误差甚至接近LSVM 算法在R=6m的平均定位误差.而对于INLCS算法,在R=12m 时,其平均定位误差优于LSVM 和LSRC算法在R=6m的平均定位误差.从图2b也很容易看出相比于LSVM和LSRC算法,NLCS和INLCS算法有更小的定位误差标准差.这些是由于NLCS算法估计节点的位置利用的是质心算法,能够充分地体现出目标节点与信标节点的空间相关性,因此NLCS算法的定位性能较LSVM 和LSRC算法更优异.此外,由于INLCS 算法利用伪跳数改进了连通信息,使各个节点到信标节点的连通信息更加准确,因此目标节点将能更准确地被信标节点所描述,从而进一步提升了算法的性能.
为了更准确地比较INLCS、NLCS、LSRC 和LSVM 算法的性能,检验各个算法的适应性,下面将考虑在较小的网络中的定位性能.假设有250个传感器节点随机分布于大小为50m×50m的区域内,其中信标节点的比例分别为5%,10%,15%,20%,节点通信半径R=6m.表1是INLCS、NLCS、LSRC与LSVM 4种算法的定位性能对比,从表1中可以看出:在4种信标节点的比例下,INLCS和NLCS算法的定位性能都优于LSRC和LSVM 算法.因此,在小网络中NLCS和INLCS算法仍然是更好的选择.

表1 小网络下的4种算法的性能对比Table 1 Performance comparison of four algorithms in small network
在实际应用场合中,无线传感器网络中存在着网络空洞,下文将进一步验证INLCS、NLCS、LSRC和LSVM 算法的适应性,考察网络中存在网络空洞时各个算法的定位性能.如图3所示为存在着网络空洞时的节点分布图,图3a为在网络中心存在着一个网络空洞时的节点分布图,网络空洞的圆心为网络感知区域中心(50m×50m),R=25m,图3b为在网络中心存在着一个大的网络空洞和网络的4角存在着4个小的网络空洞时的节点分布图,中心的网络空洞的圆心为网络感知区域中心(50m×50m),半径为100/6m,4个角上的空洞半径为100/12m.
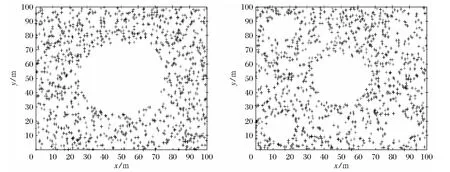
图3 空洞下的网络节点分布图Fig.3 Distribution of network nodes with holes
图4为在1 000个传感器节点随机分布于大小为100m×100m的区域内,其中信标节点的比例分别为5%、10%、15%、20%,节点通信半径R=6m,并存在如图3a、图3b所示的网络空洞下的定位性能对比图.从图4中可以看出:在4种信标节点的比例下,INLCS、NLCS算法的定位性能都优于LSVM、LSRC 算法,INLCS 算法的定位精度远优于其他3种算法,而NLCS算法稍优于LSRC和LSVM 算法,但是在节点比例较低时,NLCS算法也将远优于LSRC 和LSVM 算法,这就说明NLCS算法的定位精度对信标的节点个数的依赖没有LSVM 和LSRC算法强.而在信标节点比例较高时,LSVM 和LSRC 算法的定位精度接近于NLCS算法,这是由于信标节点的比例越高,LSVM 和LSRC的样本数越多,其分类就越精确,从而使LSVM 和LSRC算法的精度得到了较大的提高.同时从图4和图2对比可以看出,空洞对4种算法均无较大的影响.
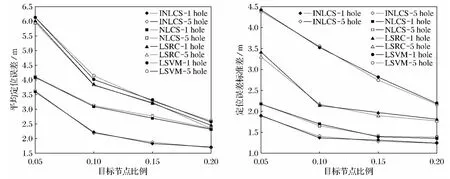
图4 存在空洞时4种算法的定位性能对比Fig.4 Comparison of positioning performance of the four algorithms
假设在一个大小为100m×100m的区域内,随机地分布着500个传感器节点,其中信标节点的比例分别为5%、10%、15%、20%,节点通信半径R=6m,并存在1个位置信息错误的信标节点时,4种算法定位性能对比如表2所示.由表2可以看出,在有1个错误的指标节点存在时,INLCS和NLCS的定位性能比LSVM 和LSRC 更为优胜,尤其是在信标节点比例较低时.这是由于LSVM 和LSRC的分类模型的建立需要所有信标节点的位置信息,一个错误的位置信息将使分类模型不准确,从而影响了所有的普通节点的定位性能,而在INLCS和NLCS中计算相关度时,只利用了连通信息,即相关系数的计算式是正确的,这样即使有错误的位置信息,也只是影响了靠近这个错误信标节点的普通节点的定位精度.

表2 存在错误节点位置时4种算法的性能对比Table 2 Performance comparison of four algorithms when there is an error node position
5 结 论
文中提出了两种新的定位算法——NLCS和INLCS.NLCS算法通过压缩感知和质心算法相结合来估计节点的位置,充分体现了节点间的空间相关性,因此NLCS算法不论在平均定位误差还是定位标准差均能表现出良好的定位性能.同时通过实验可以发现NLCS 算法对信标节点比例的依赖性不强,在较小的比例下就能取得较好的定位性能,换句话说,该算法可降低网络的定位成本,能更为广泛地适用于无线传感器网络定位.另外,NLCS算法在节点定位过程中,计算信标节点对目标节点的权值影响时,并不使用信标节点的位置,而仅仅使用节点间的连通信息,这样少数位置信息不准确的信标节点对大多数普通节点的定位并不会产生太大的影响,因此NLCS算法具有更好的鲁棒性.同时,由于采样字典由各个信标节点自身的采样原子组成并进行了压缩,这将降低网络中各节点的能耗,进而降低了整个网络的通信消耗.而且不需要头信标节点去建立定位模型,因此能更好地均衡网络的能耗.
同时,为了进一步提升算法的定位性能,文中提出了利用伪跳数来改进NLCS 算法,得到了INLCS算法.该算法在继承NLCS算法优点的情况下,利用伪跳数来更精确地描述各个节点之间的空间连通关系,从而使稀疏分解更加准确,因此算法的性能得到了进一步地提升.当然,在实际应用中还应该进一步考虑节点的能量,相比NLCS算法,INLCS算法要消耗更多的能量去获取伪跳数.因此,对定位性能与节点能量的均衡考虑将是我们进一步的研究方向.
[1]孙颖.基于蚁群算法的能量均衡传感网地理信息路由[J].沈阳大学学报:自然科学版,2012,24(2):57-61.(Sun Y.Geographic Routing of Energy Balance Sensor Network based on Ant Colony Algorithm[J].Journal of Shenyang University:Natural Science,2012,24(2):57-61.)
[2]Xu Y X,Gao X,Sun Z Y.WSN Node Localization Algorithm Design Based on RSSI Technology[C]∥International Conference on Intelligent Computation Technology and Automation(ICICTA ),2012.Zhangjiajie:[Unknown]556-559.
[3]Zhu S H,Ding Z G.Joint Synchronization and Localization Using TOAs:A Linearization Based WLS Solution[J].IEEE Journal on Selected Areas in Communications,2010,28(7):1017-1025.
[4]Shi H Y,Gao J Z.A New Hybrid Algorithm on TDOA Localization in Wireless Sensor Network[C]∥IEEE International Conference on Information and Automation(ICIA),2011.Shenzhen:[Unknown],606-610.
[5]Chan F K,Wen C Y.Adaptive AOA/TOA Localization Using Fuzzy Particle Filter for Mobile WSNs[C]∥IEEE Vehicular Technology Conference,2011.Budapest:[Unknown],1-5.
[6]Bulusu N,Heidemann J,Estrin D.GPS-less Low Cost Outdoor Localization for Very Small Devices[J].IEEE Personal Communications Magazine,2000,7(5):28-34.
[7]Wang J,Urriza P,Han Y X.Weighted Centroid Localization Algorithm:Theoretical Analysis and Distributed Implementation[J].IEEE Transactions on Wireless Communications,2011,10(10):3403-3413.
[8]杨新宇,孔庆茹,戴湘军.一种改进的加权质心定位算法[J].西安交通大学学报,2010,44(8):1-4.(Yang X Y,Kong Q R,Dai X J.An Improved Weighted Centroid Location Algorithm [J].Journal of Xi’an Jiaotong University,2010,44(8):1-4.)
[9]He T,Huang C,Blum B M.Range-free Localization Schemes for Large Scale Sensor Networks[C]∥Proceedings in MobiCom'03,San Diego,CA,USA.New York:ACM,81-95.
[10]Meertens L,Fitzpatrick S.The Distributed Construction of a Global Coordinate System in a Network of Static Computational Nodes from Inter-Node Distances[R].Palo Alto,CA,USA:Kestrel Institute,2004.
[11]Tran D A,Nguyen T.Localization in Wireless Sensor Networks Based on Support Vector Machines[J].IEEE Transaction on Parallel and Distributed Systems,2008,19(7):981-994.
[12]Qiu J F,Zhang H R.A Dictionary Classification Approach For Wireless Sensor Network Localization[C]∥Proceedings of IEEE Youth Conference Information,Computing and Telecommunication,2009.Beijing:[Unknown],23-26.
[13]Yang Z,Liu Y H,Li X Y.Beyond Trilateration:On the Localizability of Wireless Ad-hoc Networks[J].IEEE/ACM Transactions on Networking,2010,18(6):1806-1814.
[14]金坚,谷源涛,梅顺良.压缩采样技术及其应用[J].电子与信息学报,2010,32(2):470-475.(Jin J,Gu Y T,and Mei S L.An Introduction to Compressive Sampling and Its Applications[J].Journal of Electronics & Information Technology,2010,32(2):470-475.)
[15]Canfes E,Plan Y.A Probabilistic and RIP Less Theory of Compressed Sensing [J].IEEE Transactions on Information Theory,2011,57(11):7235-7254.
[16]Chen S B,Donoho D L,Saunders M A.Atomic Decomposition by Basis Pursuit[J].SIAM Journal on Scientific Computing,1998,20(1):33-61.
[17]Mallat S,Zhang Z.Matching Pursuit with Timefrequency Dictionaries[J].IEEE Transactions on Signal Processing,1993,41(12):3397-3415.

