协同优化计算方法的分析与改进

李海燕，李永缙，田 英

（1.东北大学 计算中心，辽宁 沈阳 110819；2.东软集团股份有限公司，辽宁 沈阳 110179）

多学科设计优化能够有效解决大规模复杂工程系统的设计问题，受到了国内外学者的广泛关注.而由斯坦福大学的Kroo教授等人提出的协同优化方法（CO），则被认为是一种较有前途的多学科设计优化方法，并已在飞行器设计的研究工作中得到了应用［1］.该优化方法具有典型的两级结构，其分解形式与工程设计分工的组织形式相一致，各学科保持了各自的分析设计自由.同时，各学科的计算具有并行性，能极大地缩短设计周期.在目前已有的多学科设计优化方法中，协同优化的学科自由度被认为是最高的.

但作为一门新兴的学科，CO在很多方面还不够完善.系统级优化中采用的一致性等式约束，是一种理想状态，而在一般情况下，系统级优化问题的可行域很可能不存在.另外，由于Kuhn-Tucker条件中的拉格朗日乘子不存在，或在最优解处学科一致性约束的Jacobian矩阵不连续，致使CO算法的系统级优化问题无法满足Kuhn-Tucker条件［2］.这些不完善之处，造成Balling和Alexandrov等［3-4］实验问题优化结果不够理想，也致使一部分研究的优化结果对初始点的选取敏感［5-6］.目前，世界上出现了一些协同优化算法的改进策略，其基于响应面的协同优化算法［7］，利用响应面来近似一致性约束函数.松弛因子法［8-9］对系统级等式约束进行松弛，将等式约束变为不等式形式.在此基础上，出现了动态松弛法［10-12］，它利用学科间的不一致信息选取松弛因子.这些改进措施都是从CO算法系统级的一致性约束表述形式上进行的改善，其优化效果仍受初始点的影响，有时系统级优化仍然无解.本文针对CO算法对初始点的选取具有敏感性的问题，从保证系统级优化可行有解的角度，对现有的算法进行了分析研究与改善.

1 协同优化算法

协同优化将复杂的工程系统设计问题，跟据现有的工程分工形式，分解成系统级和学科级两级优化结构.系统级负责规划协调，通过一致性约束来协调各学科的优化结果.在学科级，各学科在满足自身约束条件情况下，使其优化结果与系统级提供给该学科的目标值的差异最小.经过系统级优化和学科级优化之间的多次迭代，最终得到一个最优的系统设计方案.CO算法结构比较简单，容易实现学科自治，各子学科间的连接通过系统级优化问题的等式约束得到加强，其算法结构框图如图1所示.

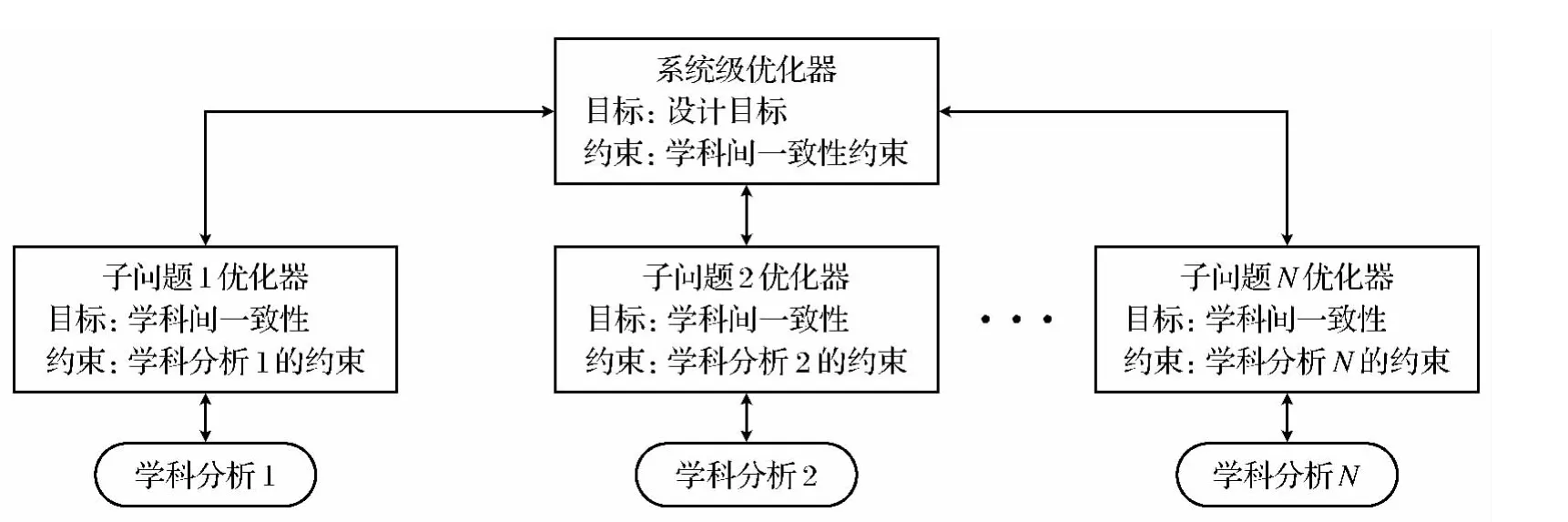
图1 协同优化算法的基本框架Fig.1 Framework of algorithm of collaborative optimization

2 CO优化过程分析与算法改进

本文以一个典型的函数优化问题为研究对象，为解决其对初始点的选取敏感性问题，对初始点在可行域内外两种情况，分别给予分析和解决.并在此基础上，提出了能够保证系统级优化可行有解的改进的协同优化算法.

2.1 典型算例

一个约束非线性优化问题的数学模型［13］为：

加入松弛因子后，其CO优化模型变为如下系统级优化模型：

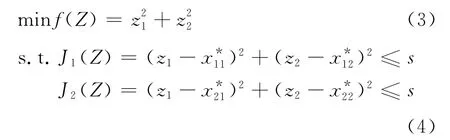
式中，z1和z2为系统级设计变量，J1（Z）和J2（Z）为系统级一致性约束，这里令β＝0.1.

2.2 优化过程分析及改进算法的提出

对初始点在系统可行域内外两种情况，分别给出优化过程分析及解决方案，从而提出了充分利用并有效结合固定松弛因子和动态松弛因子的改进算法.

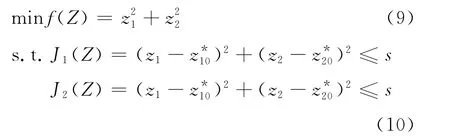
两个子学科返回的最优值相同，学科间已不存在不一致信息，若采用动态松弛法进行求解，计算所得的s值为0，程序运行一次即会结束，系统级优化结果为给定的初始值Z＝），目标值函数值为f（Z）＝＋.在这种情况下，除非给定的初始值为最优解，否则得不到最优函数值.因此，动态松弛法不适合求解初始点在可行域内的优化问题.

此时两子学科的返回值相同，只要满足s＞0，即可保证系统级优化有解.采用固定的松弛因子，对系统级进行优化求解.本文对给定初始点（1，2）进行了计算，计算结果为x＝［0.295 4，1.970 4］，f（x）＝3.969 7.

此时学科间不一致信息较大，故应采用动态松弛法，随着优化过程的进行，根据两学科间不一致信息，动态地调整s的值.采用动态松弛法，进行了3次试验，优化结果如表1所示.

表1 动态松弛法的优化结果Table 1 Optimization results of dynamic relaxation

从表1可以看出，动态松弛法的特点是运行次数少，但是精度不高，其优化结果与真实值相差比较大.同时，从结果数据可以看出，优化结果在学科级约束的边界附近.以初始点（100，2）为例，分别从学科级优化和系统级优化两个方面，对这种情况做出解释.

①学科级优化.根据学科级约束，易知点（100，2）在学科2的可行域内，经第一次学科级优化后，学科2返回的优化值为系统级分配的初始期望值（z＊10，z＊20）.由于该点不在学科1的可行域内，从学科级优化的几何意义可知，学科1的优化过程即为在学科1的可行域内，寻找距系统级期望值距离最近的点，因此点（x＊11，x＊12）在学科1可行域的边界处取得，如图2所示.

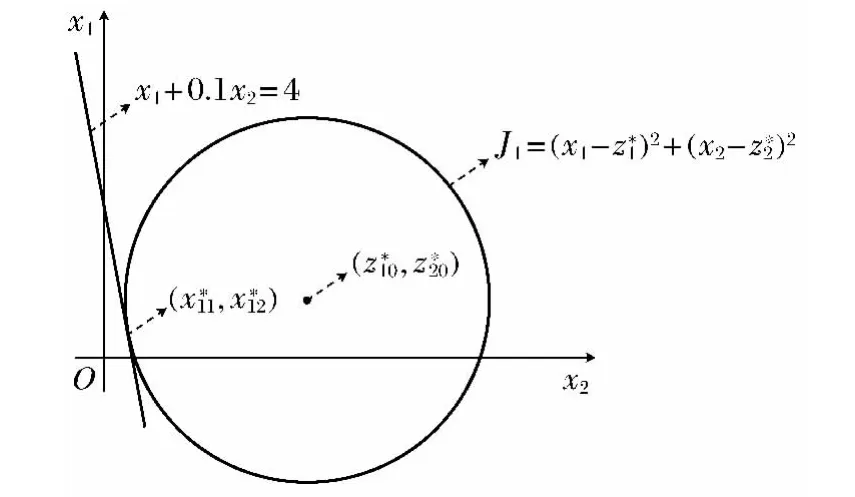
图2 学科1优化示意图Fig.2 Optimization sketch of discipline 1

② 系统级优化.学科级优化后，优化结果返回到系统级，进行系统级优化.从系统级优化的表述式（4）可知，目标函数在系统级两个约束的公共部分内寻优，如图3所示.λ＝0.5时，两圆相外切，λ＝1时，两圆互过圆心.因0.5＜λ＜1，致使系统级两个约束的相交部分，不包括学科1可行域内的点.以后的迭代过程与第一次类似，整个优化迭代过程中，学科1返回的优化值一直在学科1的边界处取得，而系统级的优化值点则一直向学科1的边界靠近，因此出现了上述运行结果.如令λ≥1，虽然有可能进入学科1，但却失去了一致性约束的意义，无法保证子学科设计变量的一致性.

图3 系统级优化示意图Fig.3 Optimization sketch of system level

从表1中的数据可以看出，此时两个子学科的优化值已经比较接近.因此此时所需的松弛因子s的值较小，可以采用固定的松弛因子，以上述运算结果为起始点，继续进行计算.计算结果如表2所示，文献［13］给出了β＝0.1时的优化结果，设计变量x＊为（0.198，1.980），目标函数f＊为3.998.从表2中数据可以看出，本文所求出的优化目标函数值较小.

表2 改进算法的优化结果Table 2 Optimization results of improved algorithm

根据初始点的选取情况，选择恰当的优化算法.当初始点选在系统可行域内时，利用固定松弛因子法求解；当初始点选在系统可行域外时，首先利用动态松弛因子法求解，然后把优化结果作为初始值，再利用固定因子法求解最终的优化结果.从以上分析可以看出，该算法可以保证系统级优化可行有解.

3 减速器设计优化算例

以减速器设计优化为例［14］，其目标是在满足转轴和齿轮大量约束的同时，使得减速器的体积最小（质量最轻），该优化共有7个设计变量，其优化问题的数学模型如下：

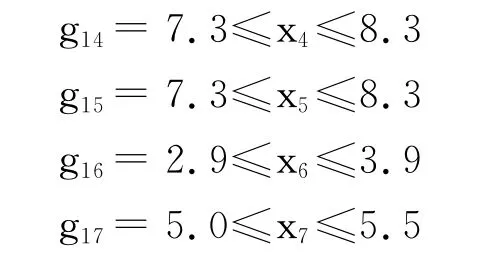
式中，x1为齿面宽度；x2为齿轮模数；x3为小齿轮齿度；x4和x5为轴承间距；x6和x7为大小齿轮的直径；g1～g2为齿的弯曲应力和接触力约束；g3～g8为轴的变形和应力约束以及由经验得到的约束；g9～g17为几何约束.可将减速器设计问题分解为并行的齿轮和轴两部分，g1～g2和g9～g17形成子优化问题1，g3～g8和g9～g17形成另外子优化问题2.

初始点选在 x0＝［100，200，300，400，500，600，200］，易知x0不在系统可行域内.首先利用动态松弛法，得到第1次优化结果.然后，以第1次的优化结果为初始点，根据第1次优化后两个学科间的不一致信息，选择s的值，利用固定因子法进行第2次优化计算，最终得到的优化数据如表3所示.文献［14］给出了该问题设计变量的优化解和最优目标函数值，其值分别为：x＝［3.5，0.7，17，7.3，7.71，3.35，5.29］，f（x）＝2 994.可以看出，本文所给出的算法符合设计精度的要求.

表3 减速器的优化结果Table 3 Optimization results of speed reducer

4 结 论

协同优化算法是多学科优化设计方法中应用最广的MDO方法，但仍有其不完善之处.本文针对CO对初始点的选取敏感问题，以一典型算例为研究对象，从保证系统级优化存在可行解的角度，对初始点在可行域内外两种情况分别进行了分析研究.

（1）当初始点选在系统可行域内时，因学科间不存在不一致信息，动态松弛法失效.在这种情况下，只要松弛因子大于零，即可保证系统级优化存在可行解，因而采用固定的松弛因子进行求解.

（2）当初始点选在可行域外时，对固定因子法和动态松弛法均得不到满意解的原因进行了分析解释.在这种情况下，首先利用动态松弛法进行优化，然后以该优化结果为初始点，采用固定因子法得到最终的优化结果.

在对典型算例的优化过程分析研究的基础上，给出了固定松弛因子与动态松弛因子有效结合的综合优化方法.该方法可以保证系统级优化可行有解，并利用该方法对减速器设计过程进行了优化，得到了较为满意的结果.

［1］ Braun R D，Kroo I.Use of the Collaborative Optimization Architecture for Launch Vehicle Design［R］.NASA-96-4018，1996.

［2］ 李鸿儒，李海龙.一种基于填充函数的神经网络全局优化算法［J］.东北大学学报：自然科学版，2007，28（9）：1247-1249.（Li Hongru， Li Hailong. A Global Optimization Algorithm Based on Filled-Function for Neural Networks［J］.Journal of Northeastern University （Natural Science），2007，28（9）：1247-1249.）

［3］ Balling R J，Wilkision C A.Execution of Multidisciplinary Design Optimization Approaches on Common Test Problems［J］.AIAA Journal，1997，35（1）：178-186.

［4］ Alexandrov N M，Kodiyalam S.Initial Results of an MDO Method Evaluation Study［R］.AIAA-98-4884，1998.

［5］ Alexandrov N，Lewis R M.Analytical Computational Aspects of Collaborative Optimization for Multidisciplinary Design［J］.AIAA Journal，2002，40（2）：301-309.

［6］ De M，Angel V.Two Decomposition Algorithms for Nonconvex Optimization Problems with Global Variables［D］.California：Stanford University，2001.

［7］ Sobieski L P，Kroo L.Collaborative Optimization Using Response Surface Estimation［R］.AIAA-98-0915，1998.

［8］ Alexandrov N M， Lewis R M. Analytical and Computational Properties of Distributed Approaches to MDO［R］.AIAA-2000-4718，2000.

［9］ Alexandrov N M， Lewis R M. Analytical and Computational Aspects of Collaborative Optimization［R］.NASA-2000-210104，2000.

［10］ 李响.多学科设计优化方法及其在飞行器设计中的应用［D］.西安：西北工业大学，2003.（Li Xiang.Multidisciplinary Design Optimization and Its Application in Aircraft Design［D］.Xi’an：Northwestern Polytechnical University，2003.）

［11］ 白小涛，李为吉.基于近似技术的协同优化方法在机翼设计优化中的应用［J］，航空学报，2006，27（8）：847-850.（Bai Xiaotao，Li Weiji.Application of Collaborative Optimization Based on Approximate Methods in Wing Design Optimization ［J］. Acta Aeronautica Et Astronautica Sinica，2006，27（8）：847-850.）

［12］ 李响，李为吉.利用协同优化方法实现复杂系统分解并行设计优化［J］.宇航学报，2004，25（3）：300-304.（Li Xiang，Li Weiji.A New Collaborative Optimization Algorithm and its Applications to Complex System Parallel Design［J］.Acta Aeronautica Et Astronautica Sinica，2004，25（3）：300-304.）

［13］ Braun R D，Gage P and Kroo I.Implementation and Performance Issues in Collaborative Optimization［R］.AIAA-96-4017，1996.

［14］ Azam S，Li W C.Multi-level Design Optimization using Global Monotonicity Analysis［J］.ASME Journal of Mechanisms and Automation in Design，1989，111（2）：259-263.