一种高效的图像增强去雾算法
李利荣, 汪 蒙
(湖北工业大学电气与电子工程学院, 湖北 武汉 430068)
雾对视觉系统的影像表现在使成像设备的输出图像对比度下降,分辨率低,这给依据图像内容的工作如目标跟踪、监控、监测等带来很大的不便.雾天图像清晰化处理有着重要的现实意义.
图像去雾技术的主要任务是去除天气因素对图像质量的影响,从而增强图像的清晰度和视见度.目前对于雾天图像进行清晰化处理的方法主要分为两类:雾天图像增强(非模型的算法)和雾天图像复原(基于模型的算法).
图像去雾技术是一个跨学科的前沿性课题,具有广阔的发展前景和应用前景,它已经成为计算机视觉和图像处理领域研究的热点问题之一,吸引了国内外许多研究人员的兴趣.本文着眼于依据图像增强的有关理论,提出一种计算简单但效果明显的实用雾天图像清晰化方法.
1 背景
图像增强根据视觉感受来改善图像效果,是个主观的图像质量改善过程.图像增强包括直方图处理、空间滤波等.
1.1 直方图均衡
直方图均衡是图像处理领域中利用图像的直方图对对比度进行调整的方法.其基本思想是把原始图的直方图变换为均匀分布的形式,从而增加像素灰度值的动态分布范围,实现增强图像整体对比度的效果.它高效且易于实现,广泛应用于图像增强处理中.
直方图均衡可分为全局化直方图均衡和局部化直方图均衡.全局化直方图是将整个输入图像的直方图做均匀分布的转化,这虽然增加整体图像像素灰度值的动态范围,增强图像整体对比度的效果,但是这对于图像中存在深度信息多变的情况,特别是有用信息分布在深度多变的场景中时,很容易使目标淹没在背景中,从而导致视频系统无法满足工作要求.局部直方图均衡的处理对象是图像的局部区域,将图像的所有局部区域依次进行直方图均衡化,增强图像局部信息.局部直方图均衡可分为子块非重叠直方图均衡和子块重叠直方图均衡.非重叠直方图均衡化的基本思想是将原图分成不重叠的子块,然后对每个子块进行直方图均衡化处理,并保留处理后的结果.相邻子块之间不重叠,大大减小了运算量,但会不可避免的出现块状效应.而重叠的直方图均衡可以大大缓解块状效应,但同时计算量也增加了.为了保证图像增强的质量,考虑降低块状效应和减少计算量,我们选择部分重叠直方图均衡化.
1.2 块状效应
块状效应:图像分块产生时,由于相邻子图块之间的灰度分布不同而产生的处理结果的差异,从而导致子块的边界出现突变的现象,视觉上有明显的块状分界线,如图2b所示.
1.3 空间滤波器
空间滤波器由一个像素的邻域(典型的是一个较小的矩形)和对该邻域包围的图像像素执行的预定义操作组成.滤波产生一个新像素值,新像素的坐标等于邻域中心的像素坐标,像素的值是滤波操作的结果.如果在图像像素上执行的是线性操作,则该滤波器称为线性滤波器.否则,滤波器就为非线性滤波器.根据需要增强图像的高频和低频特征,空间滤波器还可以分为高通滤波器(即锐化空间滤波器)和低通滤波器(即平滑空间滤波器).
2 有雾图像增强算法
正如1.1所述,本文采用的部分重叠局部直方图均衡化方法,在此基础上针对有时出现的块状效应,采用合适的线性滤波去除.
2.1 子块部分重叠直方图均衡化算法
2.1.1算法基本思想子块部分重叠直方图均衡化:先定义一个大小合适的移动子图块,以某种确定的步长来移动经直方图均衡化处理过的子块.例如,将移动步长设为子块的一半,如图1中,假设图像平均分成3×3的9个区域,a,b,e,d4个区域构成一个处理子块1(图1a),对这个子块进行直方图均衡化,然后向后移动半个子块的大小,在b,c,e,f构成的子块2里再进行直方图均衡化(见图1b),该行处理完后再转到下一行进行处理,在d,e,g,h构成的子块3里进行直方图均衡化,然后向后移动半个子块的大小,在e,f,h,i构成的子块4中进行直方图均衡化.至此,完成了整个图像的处理.

图 1 部分重叠运算示意图
下面对这9个小区域组成的部分进行分析.正中间的e区域受邻域8个区域a,b,c,d,f,g,h,i的影响.设每个子块1,2,3,4的直方图均衡化函数分别为T1(rk)、T2(rk) 、T3(rk)、T4(rk),由于区域e中的像素在整个过程中被处理了4次,所以区域e的子块部分重叠直方图均衡化函数为
(1)
每一个子块的直方图均衡化函数如
(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)
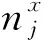

(10)
因为



(11)
由此可见,在用子块部分重叠直方图均衡化处理图像时,从效果上来看,相当于用一个模板(见图1(c))作用于这个图像的小区域(不是实际处理的子块)产生当前处理小区域的灰度概率密度函数,然后用这个概率密度函数对这个小区域进行传统意义上的直方图均衡化.
2.1.2算法实现及分析先对算法实现说明几点:
1)移动步长的设定应与子块的大小成比例,这是为了保证子块移动能产生合理的模板算子.
2)移动步长应能整除整幅图像的尺寸大小M,N,否则算法会遗漏部分边界点;
3)子块的尺寸大小与块状效应有关:若增大子块,而保持步长与子块的比例不变,则子块的重叠面积将相应减少,这将使块状效应更为严重,这时需要用改进的算法进行局部修正.对图像进行上述的部分重叠直方图均衡化处理,为了便于观察,采用不同子块大小不同步长对同一幅图像进程处理,观察效果.
具体效果对比见图2.

(a)原图

(b)160×160子块,1/16步长处理效果

(c)160×160子块,1/8步长处理效果

(d) 80×80子块,1/16步长处理效果

(e) 80×80子块, 1/8步长处理效果图 2 子块部分重叠均衡化算法处理结果对比
图2反映出了不同子块大小和移动步长对图像效果的影响.总体来说,部分直方图均衡化大大提高了图像的对比图,增强了图像细节,去雾效果明显,这对于户外监控等应用视觉系统非常有用.子块部分重叠与块重叠直方图均衡化算法相比,在保证局部对比效果较好的情况下,大大减少了计算量.但此方法采用子块部分重叠还是会因为图像块信息的差异产生少量的块状效应,且子块重叠的多少与块状效应和运算量密切相关:子块的重叠程度越小,平滑效果越差,块状效应越明显,但运算量却会急剧减小;反之亦然.
2.2 块状效应的平滑处理
由上一章分析及实验知,雾天图像经部分重叠直方图均衡化处理后,在某些子块的边缘仍然会出现不同程度的块状效应.为消除这种块状效应,使处理后的图像更清晰,需做一些平滑滤波处理.普通的线性平滑滤波器的输出是包含在滤波器模板邻域内的像素的简单平均值.图3a显示了一个3×3平滑滤波器.
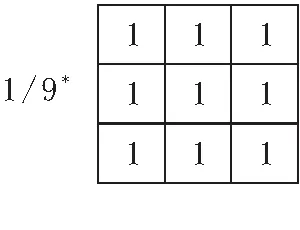
(a)3×3线性平滑滤波器

(b)对图2(e)经线性平滑后的效果图 3 线性平滑滤波器原理及其滤波效果
从实验效果可以看出,图像经线性平滑滤波器处理后,块状效应基本消失,且计算简单.本章是为了达到去除方块效应而设计的.对于方块不太明显的可以采用小模板的线性平滑.
3 总结与展望
本文提出一种简单快速的图像增强去雾方法.该方法基于图像的直方图均衡化原理,对于局部直方图均衡化方法扬长避短,采用部分重叠直方图均衡化,并可以根据需要调整步长,从而调整重叠比例来达到最好的去雾增强效果.从理论上分析子块重叠直方图均衡化算法处理图像的效果相对最好,但其运算量大,运算速度慢;子块非重叠直方图均衡化算法运算速度快,运算量较小,但处理后的图像会出现严重的块状效应,效果不清晰;而子块部分重叠直方图均衡化算法结合了前两种算法的优缺点,能获得与子块重叠直方图均衡化相当的对比度增强效果,又具有子块非重叠局部直方图均衡化的低运算量,并且一定程度上消除了块状效应.这在实验中得到了验证.基于本方法对于亮度区域性分布明显的图像仍然有微弱块状效应,我们设计了线性平滑步骤,进一步增强了效果.
[参考文献]
[1] 张汗灵,MATLAB在图像处理中的应用[M].北京:清华大学出版社,2008.
[2] 罗颖,昕雾天低对比度图像增强方法的研究[D].天津:天津大学图书馆,2005.
[3] 朱遵尚,图像增强技术研究[D].长沙:国防科学技术大学图书馆,2009:1 101.
[4] 禹晶,徐东彬,廖庆敏,图像去雾技术研究进展[J].中国图像图形学报,2011,16(09):1 561-1 576.
[5] 王玉灵,基于双边滤波的图像处理算法研究[D].西安电子科技大学图书馆,2010.
[6] 杨万挺,基于局部信息特征的雾天图像增强算法研究[D].合肥工业大学图书馆,2010.
[7] 艾明晶,戴隆忠,曹庆华.雾天环境下自适应图像增强去雾方法研究[J].计算机仿真,2009,26(07): 244-247.
[8] 彭玉华.基于离散正交小波变换的图像去噪方法[J].中国图像图形学报,1999,4(08):677-679.
[9] Rafael C. Gonzalez, Richard E. Woods, digital image processing[M].3rd Edition[S.l.]Prentice Hall ,2010.
[10] Bolet J P,Cowen A R, Launders J.Progress with an “all-wavelet” approach to image enhancement and de-noising of direct digital thorax radiographic images[J]. Image Processing and Its Applications, 1997.
[11] Economopoulos T L,Asvestas P A, Matsopoulos GK.Regional Partitioned Iterated Function Systems for digital image enhancement, Image Processing Theory[C]. Tools and Applications (IPTA), 2012 3rd International Conference on, 2012,265,269:15-18.
[12] Jong-Sen Lee.Digital Image enhancement and noise filtering by use of local statistics[J]. Pattern Analysis and Machine Intelligence, 1980,2(02):165-168.
[13] A. I. Anthis and A. P. Cracknell.Use of satellite images for fog detection (AVHRR) and forecast of fog dissipation (METEOSAT) over lowland Thessalia, Hellas[J]. Int. J. Remote Sensing, 1999,20(06):1 107-1 124.