基于zemax的新型折返式卡塞格林望远镜系统设计

钱 超， 张金业

(湖北工业大学理学院， 湖北 武汉 430068)

计算机技术的发展不仅使光学设计工作从繁杂性和庞大的计算工作中解放出来，而且给光学设计带来了新的活力．光学设计问题从数学角度看，就是建立和求解像差方程组[1]．卡塞格林望远镜因其能在较小的结构尺寸内获得较长的焦距，所以其在天文观测以及激光雷达回波的接收领域有着广泛应用．但是由于非球面镜的加工难度及成本问题，制造一台口径大的卡塞格林式望远镜的工艺要求极其严苛，加工工艺以及非球面镜的质量将直接影响望远镜的成像质量．相比较而言球面镜的加工则相对容易得多，再加上校正透镜来校正球面镜在非傍轴区产生的像差，则可大大降低卡式系统的加工难度和加工成本．

1 卡塞格林望远镜基本结构和工作原理

反射式望远镜通常由主镜和次镜构成，卡塞格林望远镜也不例外．其主镜为抛物面的凹面反射镜，次镜为双曲面的凸面反射镜．主镜抛物面的焦点与次镜双曲面的左焦点重合，这样入射的平行光将汇聚在双曲面的另一焦点处．这种类型的望远镜系统在后来的许多领域都有过广泛的应用[2]．

随着科技的发展，卡式系统的结构不断得到改进，随之出现加施密特校正板的卡塞格林望远镜、Maksutov卡塞格林望远镜等带有折射元件的卡塞格林望远镜，以增大视场．这种类型的望远镜后来被定义为折反射光学系统望远镜．

2 基于Zemax的设计

2.1 初始结构

在设计之初只要给出系统的筒长和像面位置，主次面的曲率半径只需给出大致的值，系统最前面的平板玻璃是折射元件的雏形．在需要加入透镜时，只要改变平板玻璃两个面的曲率半径即可，由几何光学的知识可知，它不会影响系统的像差及色差．这块平板玻璃还有另一个作用：在设计之初，它并不产生像差，所有的像差均由主次镜的球面镜产生；在改变其两个面的曲率半径即加入校正透镜后，通过观察评价图表可以看出其像差的明显变化，这些变化就是由于透镜校正了部分像差．所以通过加入这块平板玻璃可方便对比系统前后的成像质量变化．

系统的初始结构如图1所示．

图 1 系统的结构示意图,cm

2.2 默认评价函数的创建

将主次镜的曲率半径设为变量后，创建默认评价函数(图2)．

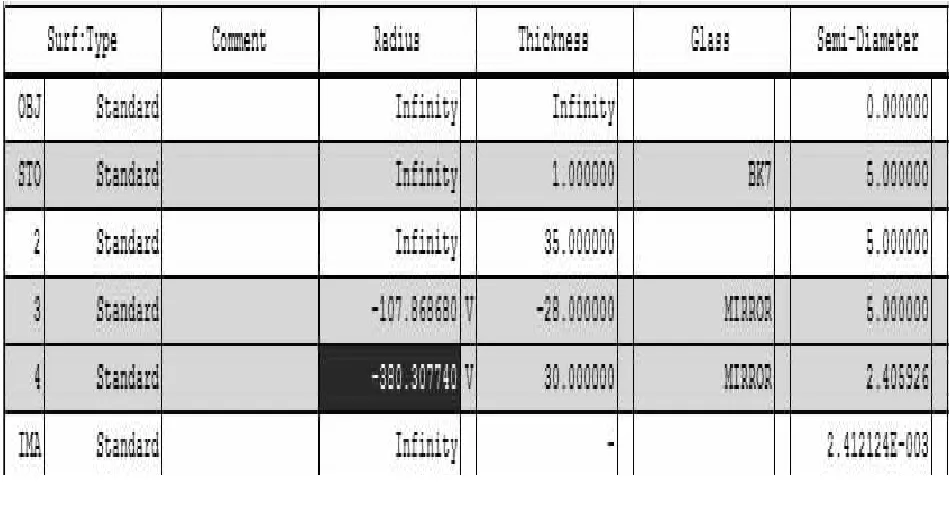
图 2 镜头编辑器

在上述镜头编辑器中，Radius表示曲面的曲率半径；thickness表示此面与下一面的距离；glass表示玻璃的类型，玻璃平板采用BK7(nf=1.52238，nd=1.51680，nc=1.51432)玻璃，图3的Default Merit Function(默认评价函数)对话框由四组选项构成:Optimization Function and Reference(优化函数和参考点)、PupilIntergration Method(人瞳积分式),Thickness Boundary Values(厚度间隔边界条件)和评价函数其它辅助选项．默认评价函数通过使用4个基本选择：优化类型、像差类型、像差计算参考点和入瞳积分方式来构建．

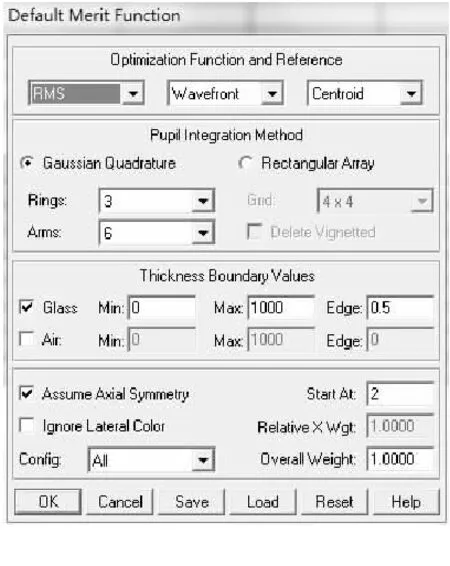
图 3 创建默认评价函数

在Optimization Function Reference(优化函数和参考点)一项中，RMS为默认的优化类型，表示评价函数由像差的均方根偏差组成 ；wavefront表示采用的像差类型为波像差，其单位为λ；Centroid表示像差计算的参考点为弥散斑的质心．

ZEMAX中像差值计算是追迹视场中代表物点发出若干条光线实现的，ZEMAX提供了两种光线通过人瞳的分布形式:高斯积分(Gaussian Quadrature)法和矩阵 (Rectangular Array)法．GQ法中通过设定轴对称入瞳面上划分的环带数(Rings)以及沿每个环上的半径臂数 (Arms ),确定每个视场和每种波长将被追迹的光线; RA法中则通过设定入瞳面上的网格(Grid )，对轴对称的入瞳按照正方形进行各种密度的抽样，确定每个视场和每种波长将被追迹的光线．如果网格上的光线落在入瞳之外，那么这条光线将被自动省略，因此实际使用的光线要比Grid的乘积少(图4)．在上面的两种算法中，GQ算法在所有实际意义的算法中具有很大的优势，它比其他方法精确并且所需要追迹的光线较少，计算速度较快，并且具有中心对称的特性，有利于减少所需要追迹的光线[1]．

图 4 两种光线的入瞳分布方式

第三栏为厚度边界值设定，用于设定评价函数中对空气间隔和(或)玻璃厚度的边界约束．第四栏为其他辅助选项，通常勾选中其中的Assume Axial Symmetry(假设轴对称)一项，这样在构造和计算评价函数时，默认评价函数将认为光学系统是左右对称和旋转对称的，此时更少的光线将被追迹，优化速度快而不降低精度．若在设计非旋转对称系统时，此项可不选．Ignore Lateral Color(忽略垂轴色差)复选框默认条件下不予选择．Start At(起始为序)用来设定Merit Function Editor(默认函数编辑器)中加入默认评价函数的操作符的起始行序．Overall Weight(全部权重)文本框:默认值为1，表示构建默认评价函数时，操作符原默认权重和权重．

设置好所有的约束条件后，点击OK生成图5的MFE(默认评价函数编辑器)．第一列为操作数序号．第二列为操作数类型：MNCG、MXCG、MNEG、MXEG操作符用来约束玻璃的边界条件；OPDX用来指定Wave,(Hx,Hy)，(Px,Py)光线相对于一个移动和倾斜的球面的光程差．该球面可以使RMS波前差最小化，ZEMAX用质心作为参考．

默认评价函数创建后调用优化，优化后系统的评价函数的值为0.0746．此值越小表示系统的性能越好(图6)．图6中：“Automatic”表示自动执行优化循环，直到系统优化不再有明显改善为止；“1 Cycle、5Cycle、10 Cycle、50 Cycle”分别表示执行1、5、10和50次优化循环；“Inf. Cycle”表示执行无限次循环，直到按下“Terminate”按钮为止；“Terminate”表示终止循环；“#CPU’s”表示分配运算的cpu核心数；“Algorithm”表示在下拉菜单中可选择合适的优化算法；“Variable”表示“设定的变量个数”．

图 5 默认评价函数

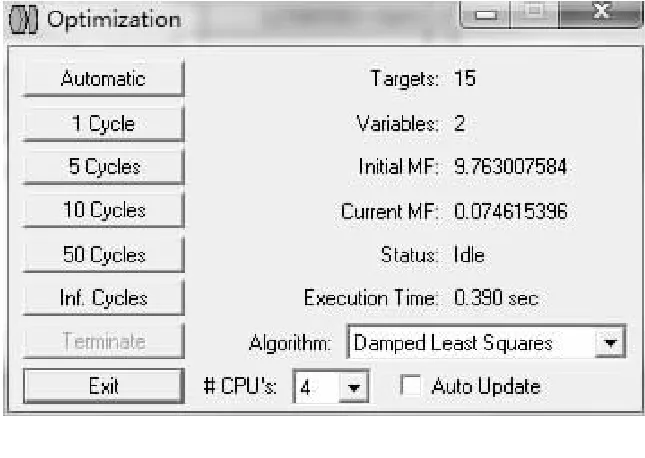
图 6 优化操作图

优化完成之后，可以通过点列图来查看初步优化后系统的成像质量如何．在理想光学系统中，经入瞳的平行光线会汇聚在像面的某点处，但在实际的成像过程中，由于球差、色差等因素的存在，经入瞳的平行光线并不能严格汇聚在像面的某点处，而是在此点处形成一个弥散斑，理论上该弥散斑的半径越小越好．在zemax中有两种对弥散斑半径的描述，它们分别是RMS Radius(均方根半径)、GEO Radius(几何半径)．前者是追迹每条光线到达像面后的坐标平方和然后再除以点的数量后再开方的值，这个值能近似反映弥散斑的质量；后者则表示弥散斑的最大半径．

光线经球面镜反射后形成的弥散斑，主要还和球面镜几何性质有关．抛物线、椭圆以及双曲线都是有焦点一说的：从抛物线凹的一面入射的平行光经抛物面反射后会汇聚在其焦点处；从椭圆一焦点发出的发散光镜椭圆面反射后会汇聚在另一焦点处；汇聚到双曲线一焦点处的光线经双曲面反射后会汇聚到另一焦点处．虽然圆却没有这种性质，但是在几何光学中可近似地认为：在傍轴条件下，其焦点在圆心与曲面顶点的中心处．这可以由物像公式[3]得出

1l'+ 1l= 2f,l'=∞，所以l=r2．

但这仅仅在傍轴条件下才成立，对于望远镜这种大孔径系统来说很难做到．

由于系统主要采用反射镜设计，而且平板玻璃不产生任何单色像差和色差，所以此时的系统是没有色差的，这在图7中得到了充分的体现，因为 F、D、C三种颜色的弥散斑是严格重合的．但是点列图的中心结构是放射状的，这说明此时系统存在着离焦，这样较大的弥散斑直径就不可避免了．

图 7 点列图

在实际的成像过程中，无穷远处的光线并不是严格的汇聚在某一点的，所以对整个入瞳而言，球面镜的球差是不可消除的．在点列图中RMS Radius 为13.76 μm；GEO Radius 为24.131 μm，这两个半径均可以通过引入校正透镜来降低．

2.3 优化后成像质量评价

初步的优化完成后，为了使系统的性能得到更大的提升，还需要对其进行更进一步的优化．在初步的优化中只引入了两个变量，即主次镜的曲率半径，这一步仅仅通过控制这两个量来减小像面上球差．现在要将透镜引入，并同时控制主次面的曲率半径，透镜的引入只要将之前的平板玻璃的两个面设为变量即可．按照上面的步骤创建默认评价函数并运行优化之后的LDE(镜头数据编辑器)如图8所示.

图 8 镜头编辑器

从图9中可以看到，此时系统的评价函数下降到0.000 34．评价函数的下降表示透镜的引入对成像质量有了较为明显的改善．

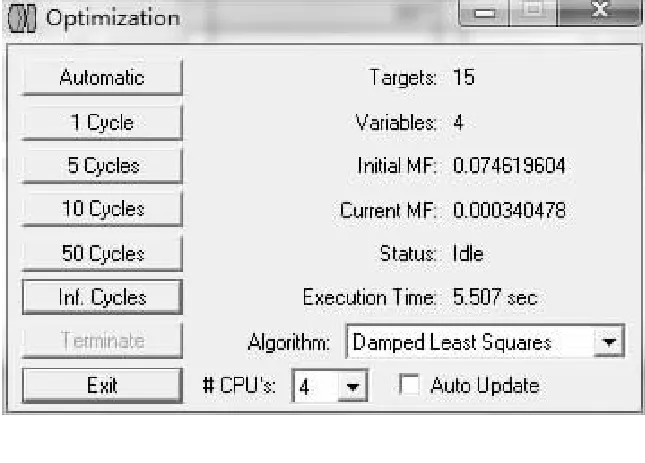
图 9 优化操作图

系统的2D结构图如图10所示.

图10 系统的2D模型

2.4 系统的图表分析

系统的结构设计及优化已经基本完成，接下来要用zemax给出的分析图表判断所设计系统的成像优劣．主要通过点列图(SPOT DIAGRAM)、光线扇面图(RAY FAN)、光程差图(OPD)以及MTF函数来分析．

图11 点列图

与图7相比，因为引入了透射元件，所以色差被引入，点列图的半径有所下降．RMS RADIUS从0.436下降到0.256；GEO RADIUS从0.977下降到0.549．这两个半径都不超过1 μm ，所以此时的色差相对而言也是很小的．点列图中心的放射状结构消失，大部分光线都集中在点列图中央，可以认为此时离焦的情况已基本消除．

图12给出了视场角为0°时的横向球差曲线．横坐标表示系统的入瞳，纵坐标为横向球差的值．从图中可以得出系统横向球差与入瞳半径的关系，原点附近曲线的斜率还可以反映系统的离焦情况．此时纵坐标的最大横向球差为1 μm，总体球差都控制在0.5 μm之内；代表F、D、C三种色光的曲线彼此之间离得很近，这说明色差是很小的；原点附近的曲率也可以证实上面点列图的判断结果．

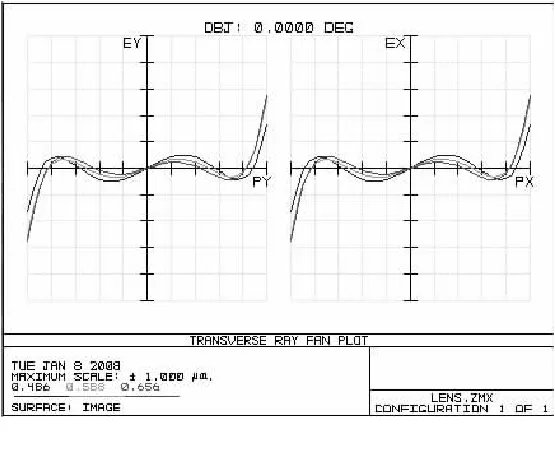
图12 光线扇面图

图13 光程差图

图13给出了系统的光程差曲线，它表示不同入瞳高度的光线经过系统后到达像面时的光程与主光线的光程之差．根据瑞利判据，当最大光程差小于波长的1/4可以认为是理想成像[4]．此时图中纵坐标的最大光程差下降到0.01个波长，远小于瑞利判据的0.25个波长．

3 最终系统设计结构

最后为了模拟次镜对光线的遮挡，在系统第一面与主镜之间加入一个半径与次镜相同的辅助镜面，并在主镜中心开一个半径为0.5 cm的圆孔以便让光线通过并与后方的目视系统衔接．最终的系统结构如图14所示．

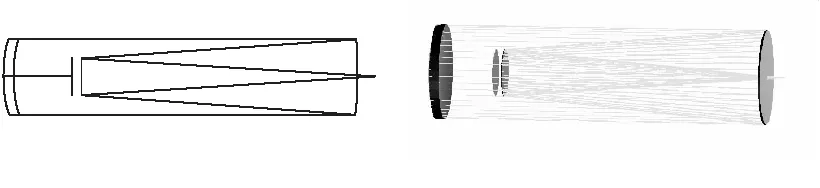
图14 最终系统的2D及3D模型

由于遮拦面的加入，MTF曲线在中频部分有所下降．

图15中，当MTF的值为0.1时，最大分辨率为229线对/mm．MTF曲线的低频反映轮廓，中频反映层次，高频反映细节．在60线对/mm处，MTF的值为0.4，此时系统能准确的反映出物体的轮廓，但是细节反映较差．

图15 MTF曲线

上面的各项图表都是在视场角为0°的情况下得出的．从图16中可以看出系统的视场角非常小的，虽然视场角的变化不大，但是MTF曲线的下降非常明显，成像质量也随之下降．这说明，系统的视场角依然非常小．小视场是卡塞格林望远镜的缺点之一，虽然本设计中的卡式望远镜的主次镜都采用球面镜，并且通过透镜校正了球面镜的球差，这虽然降低了成本和加工难度，但是系统的视场并没有因此而变大．

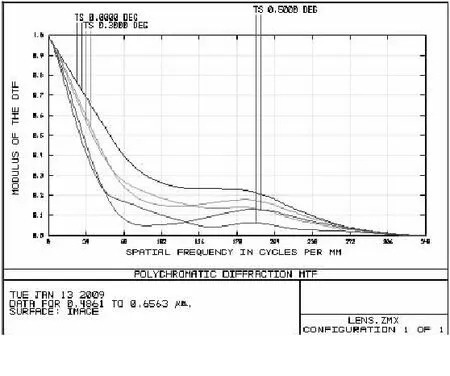
图16 视场角分别为0°、0.3°、0.5°时的MTF曲线

4 结束语

采用球面镜的卡塞格林系统，降低了系统镜面的加工难度和加工成本，并且利用透射元件校正了两球面镜的固有球差．在视场角为0°时，从各项分析图表来看，该系统具有较好的成像质量，但是当视场角变化很小时，成像质量便有了较严重的恶化，该缺点可以通过增加更复杂的前置透镜组和后置透镜组来解决，这是以后工作中所要解决的问题．

[参考文献]

[1] 迟泽英，陈文建.应用光学与光学设计基础[M].南京：东南大学出版社，2008：467-501.

[2] 潘君骅.一个新的泛卡塞格林望远镜系统[D].江苏：苏州大学图书馆，2007.

[3] 张以谟.应用光学[M].北京：电子工业出版社，2008：345-360.

[4] 刘 钧，高 明.光学设计[M].北京：国防工业出版社，2012：10-95.