遗传算法在高负载XMPP中的路径优化应用

陈双喜 吴湘莲 蔡向东 党中华

(嘉兴职业技术学院 信息技术分院，浙江 嘉兴 314036）

XMPP(Extensible Messaging and Presence Protocol，可扩展消息与存在协议)是目前主流的四种即时消息(IM：Instant Messaging)协议之一。它是一种基于XML的协议，继承了XML灵活性和扩展性。目前，XMPP采取Pastry算法进行路径优化[1,2]。物联网研究领域曾有提议，将XMPP作为物联网通信标准[3]。但是碍于在高负载条件下 Pastry算法对消息传输没有进行延时控制，可能会导致垃圾信息充斥整个网络，使得网络性能下降。因此有必要对XMPP路径优化问题进行探讨。

遗传算法（Genetic Algorithm）是一类借鉴生物界的进化规律演化而来的随机化搜索方法。它采用概率化的寻优方法，能自动获取和优化搜索空间，自适应地调整搜索方向，不需要确定的规则。目前，遗传算法已被成功应用到规划、控制、设计等领域用来求解实际问题，并且展现出广泛的应用前景[4-6]。在XMPP网络中，路径选择具有很强的随机性和复杂性。高负载条件下，如果网络能够自动优化路径，网络的工作效率将得到提高。因此本文采用遗传算法来尝试解决XMPP在高负载条件下路径优化问题。

1 高负载路径优化问题

1.1 问题描述

高负载路径优化问题描述为：已知数据包在XMPP网络中的起始节点和目标节点间传送，求数据包从起始节点到目标节点的最优路径。其中最优路径需满足以下条件：

（1）起始节点和目标节点不属于同一条线路；

（2）从起始节点到目标节点的路径必须是连通的；

（3）从起始节点到目标节点的路径中不允许有回路。

实际应用中的XMPP系统规模比较复杂[7]，我们在求解优化路径时需先对其进行简化。

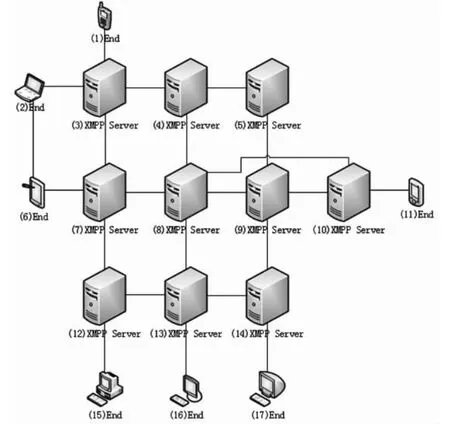
图1 简化的XMPP系统结构

在简化的XMPP系统结构图中，我们将XMPP网络上的所有节点分为：服务器节点和终端节点。其定义如下：

定义1：完成XMPP数据转送、备份、路径选择等处理操作的设备的称为“服务器节点”。如图1中的XMPP Server节点；

定义2：完成客户端数据接收、发送、数据协议转化等操作的节点称为“终端节点”，如图1中的End节点。

根据上述定义，路径可以分为服务器节点到服务器节点、终端节点到服务器节点以及服务器节点到终端节点三类路径。由于后两类路径不需要其它服务器节点进行传递，其路径的求解可以转化为对第一类路径的求解，因此在建立XMPP网络路径模型时只需考虑服务器节点与服务器节点间的最优路径。

1.2 简化的XMPP网络模型

简化后的XMPP网络模型用有权无向图G=（V，E，C）来描述，其中：

（1）V是XMPP网络中终端节点和服务器节点的集合。用一组从1开始的连续自然数逐条对XMPP网络中的不同节点进行编号，每个节点拥有唯一的编号。因此，V是由一组连续的自然数组成的集合；

（2）E 是图中边的集合，边（i，j）表示节点 i和 j之间存在线路；

（3）C=[Cij]是权值矩阵。 Cij表示边（i，j）上的权值，即从节点 i到节点j之间执行效率。取值范围为大于等于零。在实际的XMPP网络模型中，边上的权值取决于所有相邻两服务器节点的执行效率。为零时表示断路，权值越大，执行效率越高；

（4）高效路径的选择依据C和E的值进行判断，权值越大，边数越少，优先选择。

图2是简化后的XMPP网络模型图：

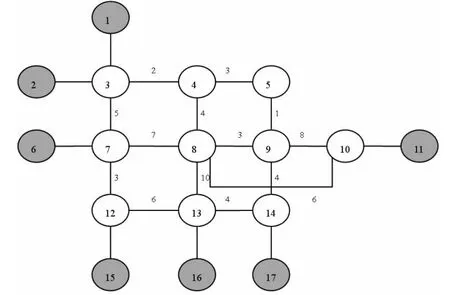
图2 简化XMPP网络模型无向图G

如上图所示，从终端节点1到终端节点16，存在多条可选路径。例如包括：（3，7，12，13）、（3，4，8，13）、（3，7，8，13）和（3，4，5，9，14，13）四条路径，这四条路径的权值和分别为：14(5+3+6)，16(2+4+10)，22(5+7+10)和 14(2+3+1+4+4)。 节点的个数分别为：4、4、4 和 6。 因此，第三条路径为优先选择路径。

2 优化路径的遗传算法

基于遗传算法的高负载XMPP优化路径主要求解流程如下：

（1）随机产生初始种群，每个染色体采取实值编码方式进行编码；（2）计算个体适应度，判断是否符合优化标准；

（3）采用自适应交叉，生产新的交叉染色体，选择适应度高的生成新个体；

（4）采用自适应变异，产生新的变异染色体，选择适应度高的生成新个体。

2.1 染色体编码

简化图节点编号作为染色体的基因值。由图2可以看出，简化图并不是一个完全连通图，图中许多节点之间并不存在边，如节点1和节点2。因此根据简化图G,定义基因之间的约束关系如下：

（1）图G中的边的集合 E中任一边（i，j），则定义基因 i与基因 j为一个基因对，记。基因对具有对称性，若存在基因对，则必存在基因对。

（2）图G中顶点集合V的任一顶点i，能够与其配对的所有基因的序列，称为该节点的邻接基因序列。如图2中节点8存在<8，4>、<8，7>、<8，9> 和<8，13>四个基因对，其对应的基因序列为{4，7，9，13}。

简化图中节点的自然路径作为染色体，并采用自然编码的方式对染色体编码。一条染色体是由某些基因组成的序列geneSequence=（S1，S2，…，Sn），其中 Si∈V，（1≤i≤n），且满足对 j（1≤j≤n-1），均是一个基因对。如染色体：

1→3→7→12→13→16

该路径中存在以下基因对：

<1，3>，<3，7>，<7，12>，<12，13> 和 <13，16>。

由于路由路径长度不一定完全相同，即不同染色体的长度并不完全相同，因此染色体长度为可变长度；另外，节点路径中不存在回路，所以染色体长度不大于简化模型G中顶点的总数17。

2.2 种群产生

文中采用带基因序列约束的方法来产生随机的初始种群，图2使用随机选择节点的方法产生初始种群时发现，其中绝大多数个体并不是一条可行路径。其算法流程如下：

输入源节点：S；目标节点：O；节点数目：Num；总节点数：N，1≤S≤N，1≤O≤N

输出染色体Gene=[Gene1,Gene2,… ,GeneNum]；

每个染色体Genei长度为Li,2≤Li≤N,1≤i≤Num

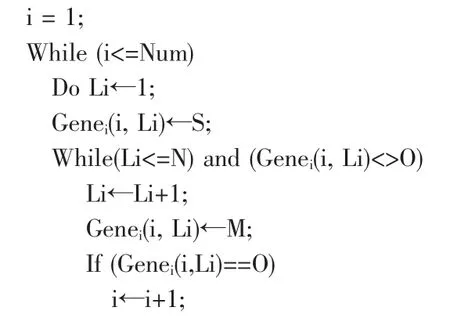
由基因对的具有对称性，上述算法通过数组机制解决路径中的回路问题。

2.3 适应度函数

文中遗传算法中的个体对应于有权无向图中求解的优化路径。节点总数越少、权值总和越大的优化路径认为是较优的个体，即权值节点比较大的路径。因此，对于不同的个体设计如下适应度函数：

F(i,j)=Cmax-Σe(i,j)/Σf(i,j)，

其中，Σf(i,j)表示路径上的所经过的节点数的总和，Σe(i,j)表示路径上的所有权值的总和，Cmax=max(Σe(i,j)/Σf(i,j))+R，表示所有路径中的最大权值节点比，其中随机自然数R为修正因子。因此，路径上经过的节点数少，总权值越大，适应函数的适应值越大；反之，越小。

2.4 选择操作

本文采用轮盘赌[8]选择方法进行个体选择，个体适应度越大，被选中的概率越大。即优化路径中经过的节点少并且权值大。表1是采用轮盘赌选择方法，修正因子R取值为10，得到的节点1到节点16的路径，具体如表1所示：

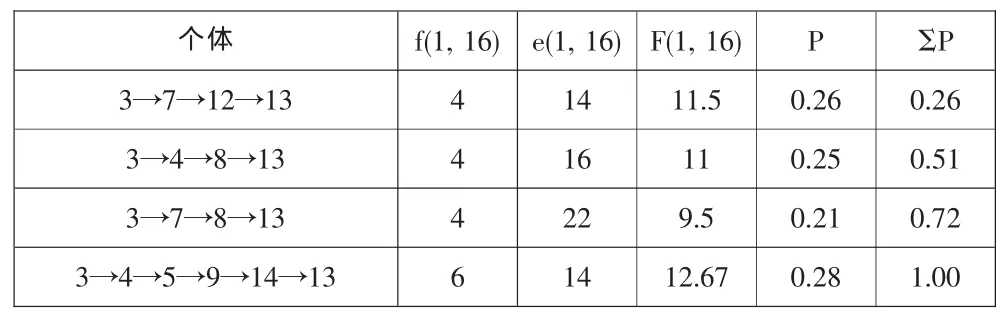
表1 节点1到节点16轮盘赌选择路径

其中P=F/ΣF。选择染色体过程中产生的随机数P∈[0,1]，按如下方法确定染色体：

当 P∈[0,0.26]，则选择染色体 3→7→12→13；

当 P∈[0.26,0.51]，则选择染色体 3→4→8→13；

当 P∈[0.51,0.72]，则选择染色体 3→7→8→13；

当 P∈[0.72,1.00]，则选择染色体 3→4→5→9→14→13

2.5 交叉操作

本文采用带基因序列限制的交叉算子，具体描述如下：

假设进行交叉的父代个体P1、P2分别为：

P1：3→7→ |8→ 13

P2：3→4→ |5→ 9→14→ 13

首先随机产生交叉位置 Location（1≤Location≤min（L1,L2）），其中L1和L2分别为P1和P2的染色体长度。假设Location=2，对染色体P1进行交叉操作时先判断处于交叉位置Location后的染色体 P2中的基因是否存在于处于交叉位置Location的基因序列中，如果存在，则进行交叉；否则，依次向后寻找P2中的基因。同理，对染色体P2进行同样的交叉操作。若P1与P2均不能进行交叉操作，则重新选择一对染色体进行交叉。P1和P2交叉后的结果为：

P1’： 3→ 7→ |5→ 13

P2’： 3→ 4→ |8→ 9→ 14→ 13

交叉后的染色体中可能存在断路，如染色体P1’。因此交叉后，需对染色体进行去环处理。

2.6 变异操作

本文采用对路径中的子路径进行变异的方法。首先，随机确定产生变异的起点 S和终点T，然后通过调用产生初始种群算法，产生一条从S→T的路径，再用该路径替代原先路径中S→T的路径，作为变异后的新个体。

假设染色体为：3→ 4→ 8→ 9→ 14→ 13，不妨设变异起点为8，变异终点为9，通过调用产生初始种群算法产生一条8→9的路径：

10

则变异后的结果为：

3→ 4→ 8→ 9→ 10→ 14→ 13

注意到产生变异后的新的染色体中可能存在环。因此，与交叉操作相同，变异后需对染色体进行去环处理。

3 试验结果

假定初始种群大小为10，交叉概率为 PC=0.8，变异概率 Pm=0.01，进化代数为10，节点1到节点16的前4条路径，其中最优路径为3→7→8→13

表2 节点1到节点16的路径列表

[1]P.Saint-Andre,Ed.Extensible Messaging and Presence Protocol(XMPP):Core[OL].http://www.faqs.org/rfcs/rfc3920.txt.

[2]黄剑.基于XMPP的端到端连接建立机制的研究与实现[D].国防科学技术大学，2009.

[3]张卫，张峻峰，罗长寿.XMPP应用于物联网通讯协议的研究[J].中国农学通报，2012，28（09）：289-292.

[4]Liu Junli,Chen Shuangxi,Mao Jie.Genetic algorithm study on the university course timetabling problem[C]//2012 IEEE International Conference on Cyber Technology in Automation,Control,andIntelligent Systems(CYBER).Bangkok,Thailand,2012:179-182.

[5]张华，王进戈.机器人避开多随机障碍物的路径规划遗传算法[J].西华大学学报，2007，26(1)：56-58.

[6]Chang Wook Ahn,R.S.Ramakrishna.A Genetic Algorithm for Shortest Path Routing Problem and the Sizing of Populations [J].IEEE TRANSACTIONS ON EVOLUTIONARY COMPUTATION Jun,2002:566-579.

[7]龚正虎，黄剑，侯婕.基于XMPP的多跳TCP连接通信方案研究[J].北京工业大学学报，2008，34(Supp):32-35.

[8]梁宇宏，张欣.对遗传算法的轮盘赌选择方式的改进[J].信息技术，2009，12(12):127-129.