基于战斗队形的坦克连多分辨率建模方法研究
杨慧杰
(中国电子科学研究院,北京 100041)
0 引言
计算机仿真在军事训练、作战指挥等领域的广泛应用推动着军事理论和技术的发展。然而,现代战争系统的复杂特点又对仿真技术的发展提出了更多更新的挑战。目前,在作战仿真训练领域,多分辨率建模技术被认为是解决战争系统复杂性与计算资源有限性之间矛盾的有效途径,也是众多专家和学者当前研究的热点内容[1,2]。
所谓多分辨率建模是指为同一个对象建立具有不同分辨率的一个模型、一族模型或者是二者的组合[3]。在作战训练系统中,不同层次上的模型要实现互联、互通、互操作,核心问题是解决同一对象不同分辨率模型之间的映射问题,也就是高分辨率模型向低分辨率模型聚合,低分辨率模型向高分辨率模型解聚[4]。目前一种最为简单的算法是完全聚合解聚发,所有实体要不都在最高分辨率下运行,要不都在最低分辨率下运行,该方法灵活性较差;另外一种是部分解聚法,即根据需要动态地将低分辨率模型部分解聚,但这种方法在确定解聚范围方面存在困难,并且往往会由于频繁的聚合解聚带来额外的资源消耗;还有一种算法即伪解聚,解聚模型不受控制、不与其他模型交互,仅拥有一些属性参数,这种算法计算代价低,在一些仿真系统中得到了应用[5]。
目前,无论是海军舰艇、空军战斗机还是陆军作战分队的仿真,战斗队形的建模和不同队形间的变换都是一个重要的研究内容。常用的队形变换和控制算法可以分为直接变换法和逼近法两类:直接变换法计算量大,比较繁琐,并且不考虑变换过程;逼近法考虑队形的变换过程,更加符合战术要求[4]。
在分析研究现有坦克连战斗队形控制算法的基础上,将队形模型应用到聚合实体内部,作为伪解聚算法的依据,给出了一种实用的基于战斗队形的聚合解聚算法,并将该算法应用到作战模拟训练系统中,证明了这种算法的可行性和有效性。
1 问题的提出
本系统中,为了降低计算量,提高仿真效率,在满足应用需求的前提下,“坦克连”通常作为一个作战单元进行仿真,即低分辨率的聚合级仿真,在这种情况下,聚合实体作为一个整体与其他实体和外部环境发生交互。然而,随着仿真的需要,聚合级的坦克连实体在某些情况下也需要分解到单车级的坦克车辆,以更高的分辨率进行计算,即解聚。例如,当侦察机从空中对地面实施侦察时,需要详细获知每一辆坦克的位置和速度、当武装直升机发射反坦克导弹时也需要具体瞄准到一辆坦克而不是整个坦克连,这时,就需要将聚合级的坦克连进行解聚获得其中每一辆坦克的具体位置和速度。
实际情况是,在训练过程中,侦察、打击等需要进行解聚的情形出现的频率是很高的,如果采用传统的完全聚合解聚算法,会造成大量的资源浪费,往往不能达到降低计算量的目的,反而会给系统带来更多的额外负担,同时,高分辨率的解聚实体并不需要被实际仿真和控制,而是仅仅具有某些属性特征即可,如可视性,能够被其他实体发现。因此,本系统中采用了既可以满足仿真训练需求,计算量又相对较低的伪解聚算法,其基本思想是实体在聚合的低分辨率环境中被仿真和控制,并与其他实体发生交互,在解聚的高分辨率环境中仅仅被描述而不受控制。
作战过程中,坦克连需要根据作战任务及地理环境的不同选择不同的战斗队形,这对于完成任务是非常重要的,因此在聚合和解聚的过程中除要考虑一致性约束外,还必须考虑战斗队形不同的影响。坦克连最常使用的战斗队形一般包括一字横队、一字纵队、左梯形队、右梯形队、楔形队、V形队,如图1所示,这也是在本系统中实现的六种坦克连战斗队形,是描述的聚合解聚算法的基础。

2 算法描述
本系统中,通常情况下坦克连都以聚合实体的形式运行在低分辨率状态下,实体的位置就是聚合体的位置,实体的速度就是聚合体的速度。在必要的情况下,根据聚合实体当前的战斗队形运行伪解聚算法,得到高分辨率伪解聚实体的位置和速度等信息。在描述解聚算法之前,先简述伪解聚算法的一致性约束,即保证同一对象的不同分辨率模型在同样的仿真条件下运行时保证其属性参数的一致性[6,7]。
2.1 伪解聚的一致性约束
2.1.1 位置约束
假定一个仿真对象O的低分辨率模型记为M1,其位置记为,高分辨率模型记为 M2,其中包含 N 个实体 E1,E2,…,En,位置记为,…,N。在 t时刻,将模型M1解聚为M2时,必须符合式(1),解聚算法才能满足位置一致性约束,也就是聚合级实体的位置必须是所有解聚实体位置的平均值。

在基于坦克连战斗队形的位置解聚算法中,除满足上述约束条件外,坦克之间的间距还必须满足标准队形中指定的数据约束。
2.1.2 速度约束
首先,类似于位置一致性约束条件,速度解聚算法中聚合体实体的速度也必须是所有解聚实体速度的均值,即满足式(2)。

此外,即使在满足式(2)的条件下,一个实体的速度也可以分解成无数组解聚实体的速度,因此,还必须对解聚速度从大小和方向两个方面进行约束。速度大小最基本也是最典型的约束条件是极值约束,即解聚实体速度的大小必须在坦克所允许的速度范围内。速度方向的约束较为复杂,解聚实体速度的方向往往与其在战斗队形中的角色或者担负的任务密切相关,同时也受到地形环境的影响,因此解聚实体速度方向的确定是相对困难的。
2.2 伪解聚算法
2.2.1 位置伪解聚算法
首先以聚合实体所处的位置为原点建立平面直角坐标系,其正前方为Y轴的正方向,正右方为X轴的正方向。相邻两车在X轴上的距离记为xoffset,Y轴上的距离记为yoffset,这是队形中预先指定的数据约束条件。
解聚之后,聚合实体所处的位置应该是整个队形的中心位置。因此,将上述六种队形的算法分为两类,一字纵队、一字横队、左梯形队、右梯形队是一类,楔形队和V形队为另一类。
对于第一类队形,基准车的位置就是聚合实体的位置,即坐标原点,左梯形队形示意图,如图2所示。
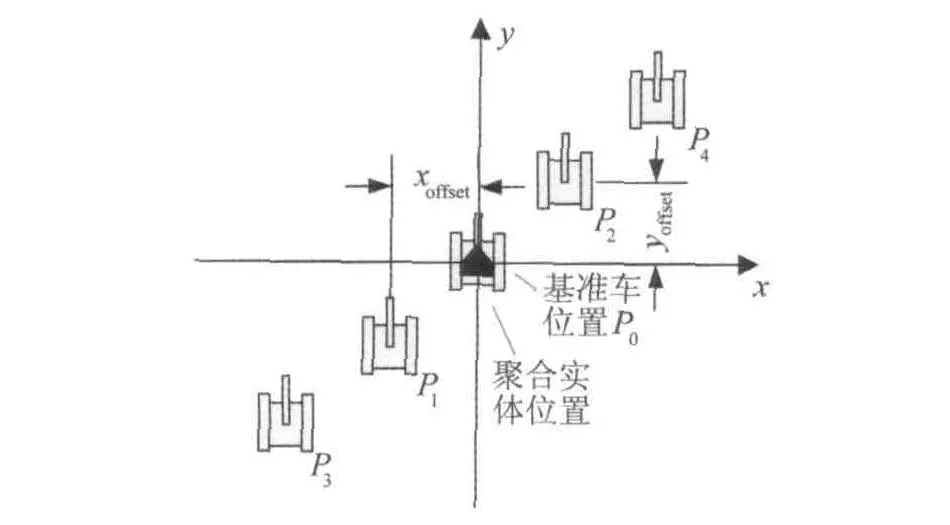
图2 左梯形队形示意图
第i辆车与基准车的相对位置Dioffset可以表示为

通过坐标变换矩阵,将Doffset_i变换到地心第四坐标系中的相对位置

记基准车在地心第四坐标系中的位置(即聚合实体的实际位置)为,则第 i辆车在地心第四坐标系中的位置可以表示为
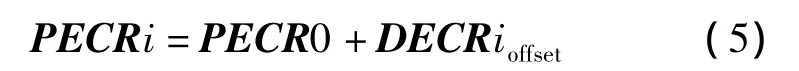
在上述算法中,当xoffset取值非0,yoffset取值为0时,即为一字横队;当 xoffset取值为0,yoffset取值非0时,即为一字纵队;当xoffset与yoffset取值同正或者同负时,为左梯形队;当xoffset与yoffset取值一正一负时,为右梯形队。
对于楔形队和V形队,基准车的位置并不是聚合实体所处的位置,如图3所示。

图3 楔形队形示意图
假定聚合实体内部车辆的总数为n,首先需要计算基准车P0与聚合实体在二维平面直角坐标系中的相对位置,如下
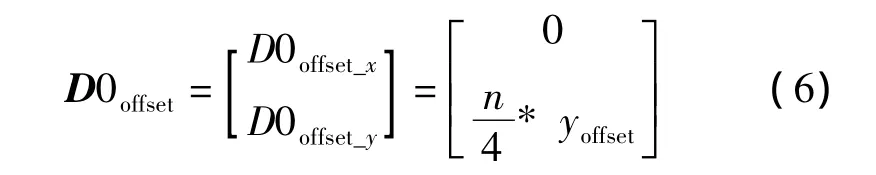
则第i辆车与聚合实体位置的相对距离可以表示为

得到第i辆车与聚合实体的相对位置Dioffset之后的算法与第一类队形相同,首先将该相对位置转换到地心第四坐标系中,再与聚合实体的地心第四坐标位置相加得到第i辆车的地心第四坐标位置,最后调整高程信息保证车辆位于地表。
2.2.2 速度伪解聚算法
基于对速度解聚约束条件的分析可以看出,设计既满足约束条件又符合实际需求的普适化的算法或者规则是很困难的,特别是解聚实体速度方向的确定方法。具体到本系统中采用的算法是直接用聚合实体的速度作为解聚实体的速度。
对于本系统来说,聚合实体是坦克连,解聚实体是单车,在战役战术级别的训练中,坦克连一般作为整体运用,不再关心其中每个解聚实体的具体任务,因此,直接采用聚合实体的速度作为解聚实体的速度是符合实际情况的。同时显而易见,这种算法也是满足2.1.2中的约束条件的。此算法虽然简单,但是至少对于本系统来说是满足应用要求的,并且计算量小、效率高。
3 结语
多分辨率建模方法是当前计算机仿真领域的热点研究内容之一,模型的聚合和解聚又是多分辨率建模方法的核心问题,是影响多分辨率建模方法在作战仿真训练中应用效果的主要因素。从目前的研究现状来看,虽然有一些理论成果,并且也在不断的发展改进,然而真正能够用到工程应用中的成果却不多。以陆军战役战术级训练系统为背景,将战斗队形运用到多分辨率建模的聚合解聚过程中,提出了一种较为有效的算法,并在实际的工程应用中加以验证,证明了这种算法的可行性和有效性。
[1]韩翃,康凤举,王圣洁.多分辨率建模在战役推演仿真系统中的应用[J].火力与指挥控制,2012,37(3):59-62.
[2]周华任,马亚平.战争模拟多分辨率建模研究[J].系统仿真学报,2009,21(21):6 833-6 836.
[3]DAVID P K,BIGELOW J.Experiments on Multi-Resolution Modeling(MRM)[R].RAND Corporation,1998.
[4]郭齐胜,杨立功,杨瑞平,等.计算机生成兵力导论[M].北京:国防工业出版社,2006:180-188.
[5]刘秀罗.CGF建模相关技术及其在指挥控制建模中的应用研究[D].长沙:国防科学技术大学,2001.
[6]朱松岩,江敬灼,叶雄兵,等.聚合解聚及其一致性问题研究[J].军事运筹与系统工程,2008,22(3):33-38.
[7]刘宝宏.多分辨率建模的理论与关键技术研究[D].长沙:国防科学技术大学,2003.

